师从江北
问题引出
归一化处理：指标的数组[a b c]归一化处理得到[a/(a+b+c),b/(a+b+c),c/(a+b+c)]
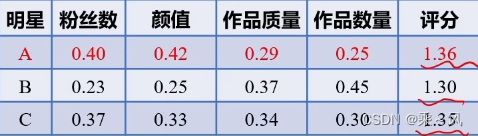
因为每个指标的重要性不同，所以要加上一个权重
如何科学的确定权重，就要用到层次分析法（AHP）
模型原理
建立递阶层次结构模型
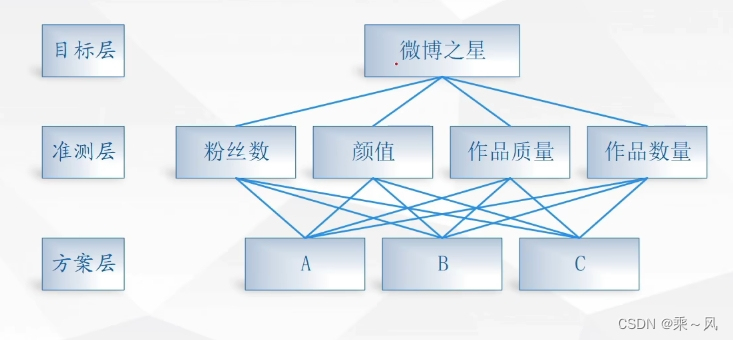
构造出各层次中的所有判断矩阵
构造判断矩阵
因两两比较的过程中忽略了其他因素，导致最后的结果可能出现矛盾
所以需要一致性检验
一致性检验
一致性检验的证明过程
一致性检验的步骤
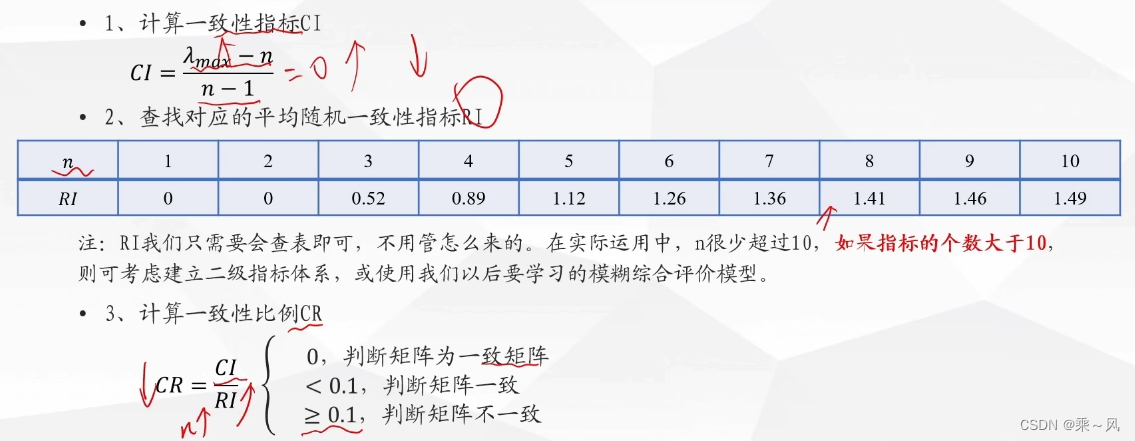
回到最初问题
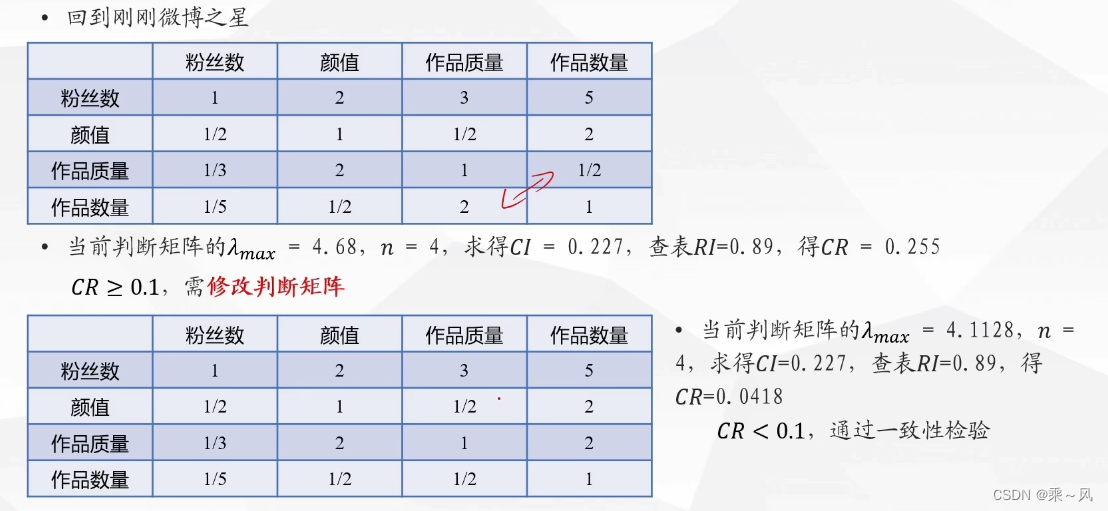
求权重
算术平均法求权重
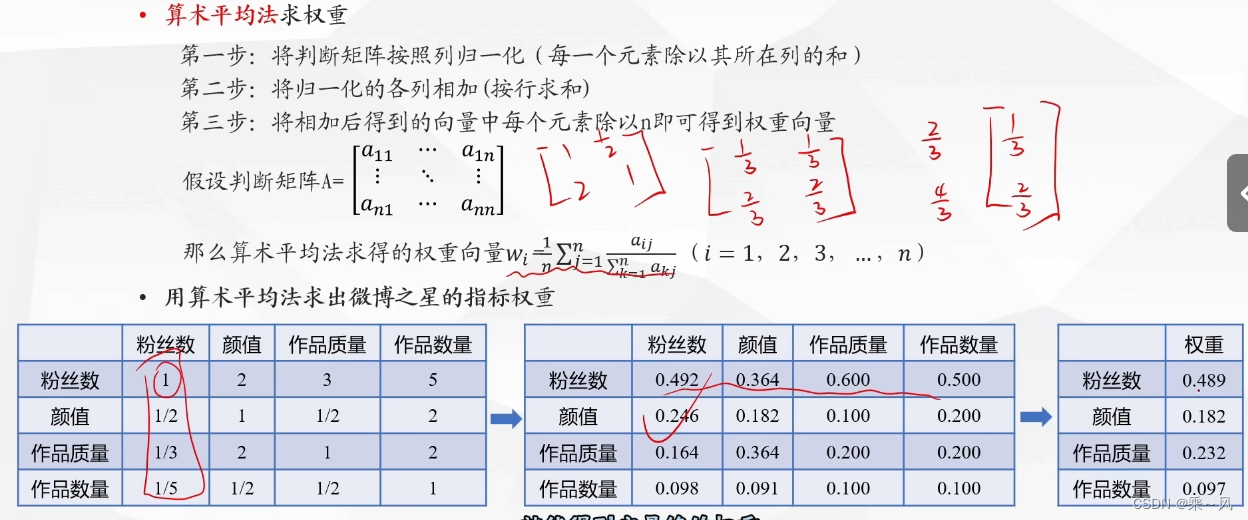
几何平均法求权重
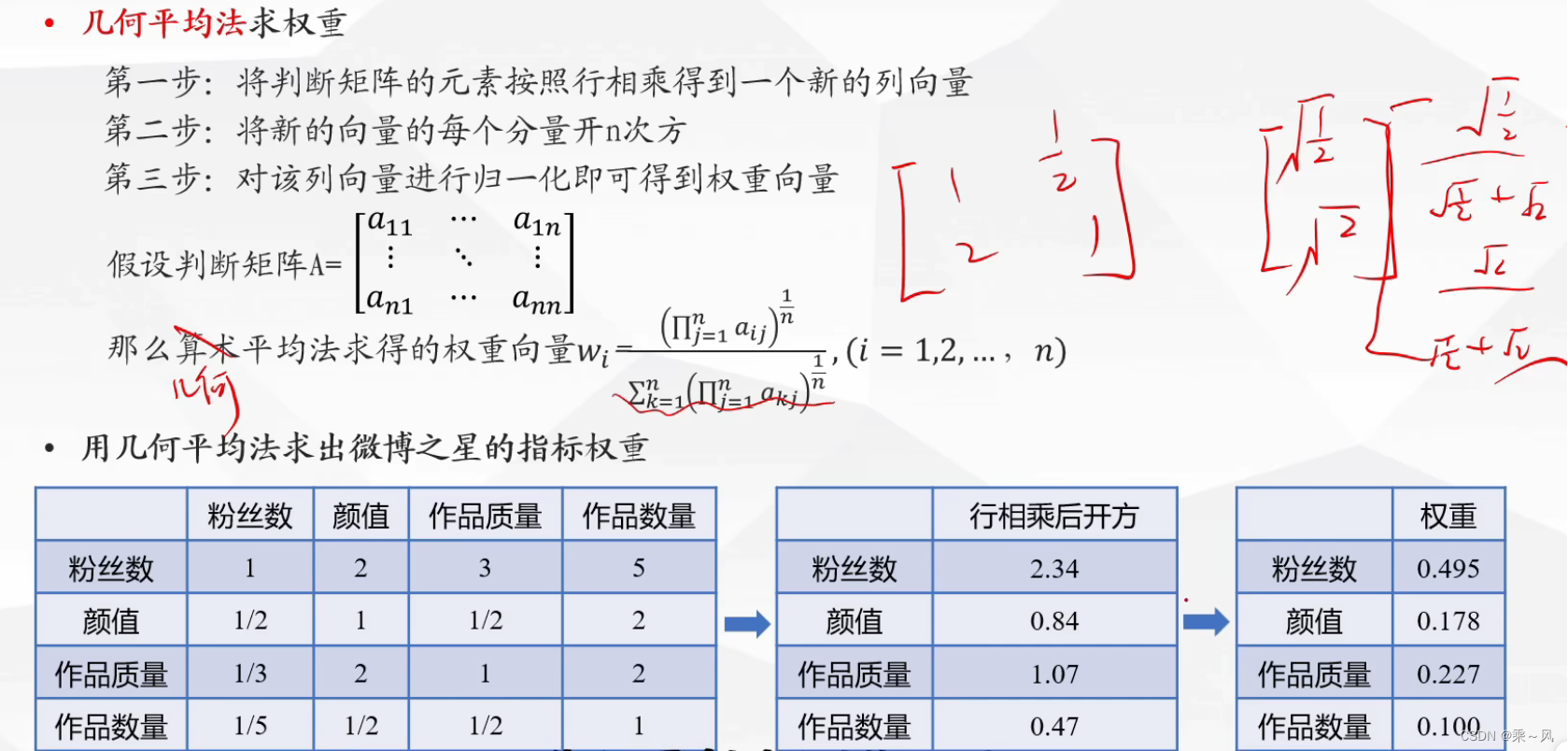
特征值法求权重
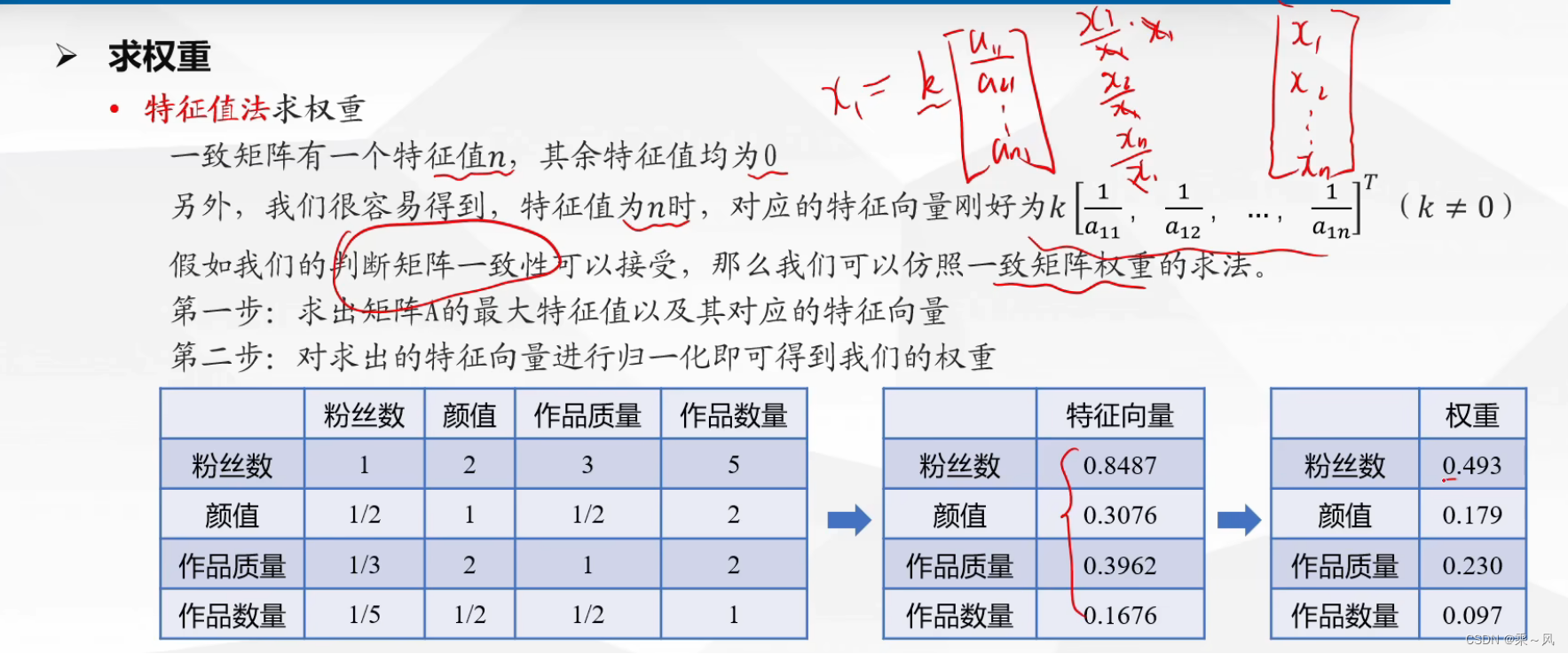
求评分
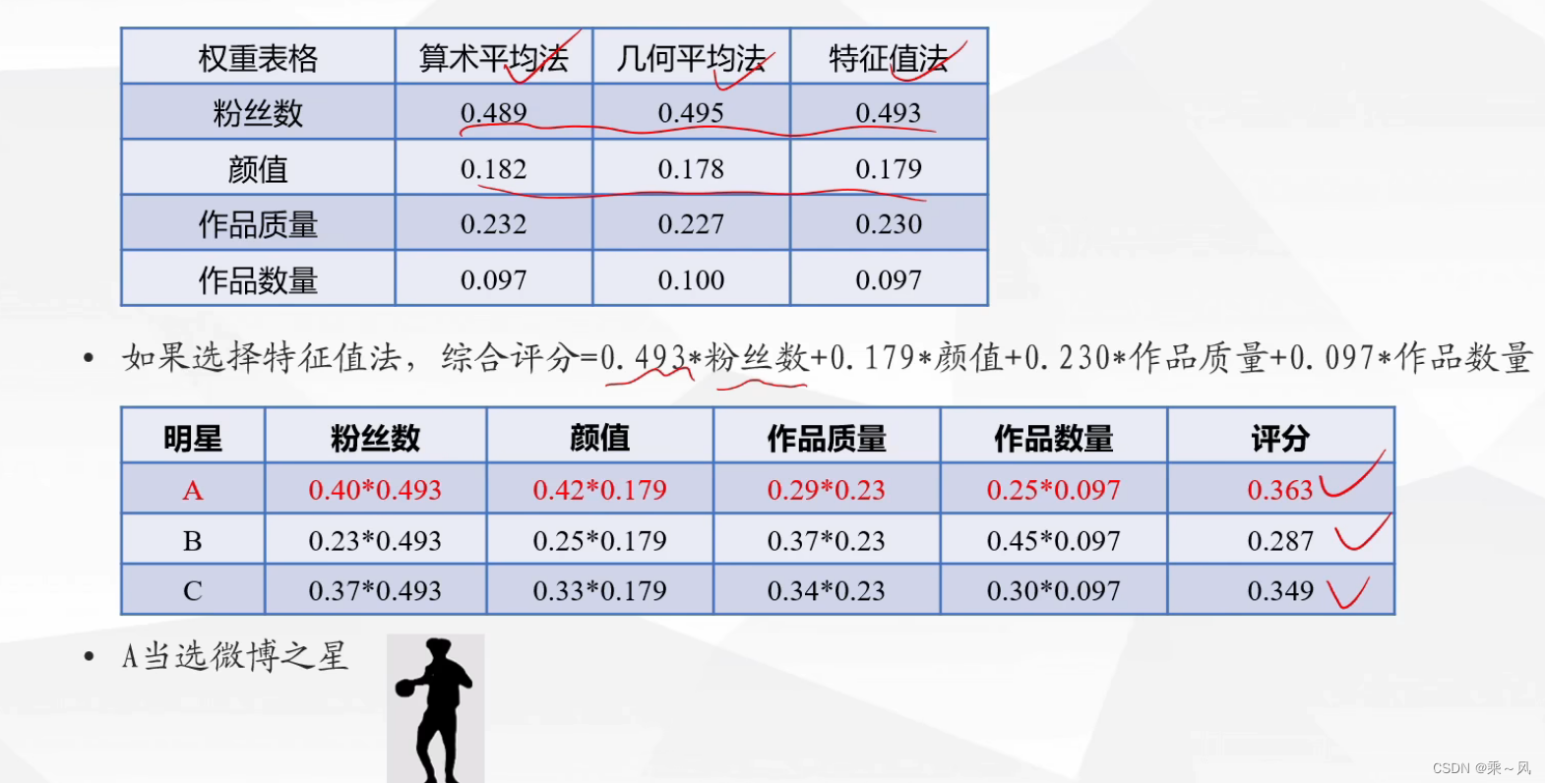
过程总结
构造判断矩阵->进行一致性检验->求权重
Python代码实现
Numpy是Python中用于科学计算和数值操作的基础库，提供了很多高性能的多维数组对象
Pandas是用来提供高性能易于使用的数据结构和数据分析工具所用的库
Matplotib是创建可视化的库，即用来绘图的
一致性检验
定义矩阵A，np.array是numpy库中的一个函数，用于创建数组，它将输入的对象（如列表，元组，其他数组等）转化为Numpy数组
"""
A=np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,2],[1/5,1/2,1/2,1]])"""
求最大特征值（Max_eig）以及对应的特征向量（eig_vec）
np.linalg.eig是Numpy库中的一个函数，用于计算方阵的特征值和特征向量
"""
eig_val,eig_vec=np.linalg.eig(A)
Max_eig=max(eig_val)"""
获取A的行为0，获取列为1，shape是获取形状信息
"""
n=A.shape[0]"""
注：这里的RI最多支持n=15
这里n=2时一定是一致矩阵，所以CI=0,我们为了避免分母为0，将这里的第二个元素改为很接近0的正数
"""
CI=(Max_eig-n)/(n-1)
RI=[0,0.0001,0.52,0.89,1.12,1.26,1.36,1.41,1.46,1.49,1.52,1.54,1.56,1.58,1.59]CR=CI/RI[n-1]print('一致性指标CI=',CI)
print('一致性比例CR=',CR)if CR<0.10:print('因为CR<0.10,所以该判断矩阵A的一致性可以接受！')
else:print('因为CR>0.10,所以该判断矩阵A的一致性不可以接受！')算术平均法求权重
import numpy as npA=np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,2],[1/5,1/2,1/2,1]])"""
计算每列的和
np.sum函数可以计算一维数组中所有元素的总和
还可以通过指定axis参数来计算多维数组的某个维度上的元素总和，例如，在二维数组中,axis=0表示按列计算总和，axis=1表示行计算总和
"""
Asum=np.sum(A,axis=0)#获取A的行
n=A.shape[0]"""
归一化，二维数组除以一维数组，会自动将一维数组扩展为与二维数组相同的形状，然后进行逐元素的除法运算
"""
Stand_A=A/Asum"""
各列相加到同一行
"""
Asumr=np.sum(Stand_A,axis=1)"""
计算权重向量
"""
weights=Asumr/nprint(weights)几何平均法求权重
import numpy as npA=np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,2],[1/5,1/2,1/2,1]])#获取A的行
n=A.shape[0]"""
将A中每一行元素相乘得到一列向量
np.prod函数可以计算一维数组中所有元素的乘积
还可以通过指定axis参数来计算多维数组的某个维度上的元素总和，例如，在二维数组中,axis=0表示按列计算总和，axis=1表示行计
"""
prod_A=np.prod(A,axis=1)"""
将新的向量的每个向量开n次方等价求1/n次方
np.power是Numpy库中的一个函数，用于对数组中元素进行 幂运算
，可以使用np.power(a,b)对数组a中的每一个元素都按照b指数进行运算
"""
prod_n_A=np.power(prod_A,1/n)#归一化处理
re_prod_A=prod_n_A/np.sum(prod_n_A)#展示权重结果
print(re_prod_A)
特征值法求权重
import numpy as npA=np.array([[1,2,3,5],[1/2,1,1/2,2],[1/3,2,1,2],[1/5,1/2,1/2,1]])#获取A的行
n=A.shape[0]#求出特征值和特征向量
eig_values,eig_vectors=np.linalg.eig(A)#找出最大特征值的索引，np.argmax是Numpy库中的一个函数，用于返回数组中最大值的索引
max_index=np.argmax(eig_values)#找出相应的特征向量
max_vector=eig_vectors[:,max_index]#找到对应的特征向量
weights=max_vector/np.sum(max_vector)#输出权重
print(weights)若有侵权，请联系作者
