计算几何领域出现于 20 世纪 70 年代,研究解决几何问题的数据结构和算法。这尤其包括确定图像内的拓扑结构,或者实际上是更高维的表示,例如点邻域,这可以帮助从数字图像数据等中导出几何意义[1]。
计算机视觉主要涉及静态或动态图像处理、理解和重建[3]。由于深度神经网络驱动的算法提供了令人印象深刻的、超人类的结果,目标识别(分类)、目标检测(分类和定位)和目标分割(分类、定位和边界检测)的计算机视觉应用领域一直受到欢迎。研究和工业界的关注不断增加。
毫不奇怪,考虑到这些重叠的兴趣领域,计算几何为计算机视觉及其对应领域计算机图形学领域提供了有用的概念。一组点的 Voronoi 图(又称为 Dirichlet 曲面细分、Voronoi 曲面细分或 Voronoi 划分)及其对偶点的 Delaunay 三角剖分(又称为 Delone 三角剖分)是此类有用概念的示例 [1, 2]。相关的计算机视觉应用包括人脸识别、人脸变形、图像合成和表面建模。在这篇博文中,我们演示了如何使用图像中人脸的 Delaunay 三角剖分/Voronoi 图作为人脸识别或人脸变形等应用的先驱。
让我们从定义开始。

NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割
1、Voronoi图
Voronoi图将域划分为一组点的最近邻域。考虑点集 P = {p₁, p2, …, pₙ} ∈ ℝ²。将 pᵢ, pⱼ ∈ P, pᵢ ≠ pⱼ 的平分线 BS(pᵢ, pⱼ) 定义为距离函数 d 中相对于 pᵢ, pⱼ 的等距轨迹,即 BS(pᵢ,pⱼ) = {q ∈ P : d( pᵢ,q) = d(pⱼ,q)}。令 pᵢ 相对于 pⱼ 的优势区域 D(pᵢ,pⱼ) 表示包含由 BS(pᵢ,pⱼ) 界定的 pᵢ 的区域。给定 P 的 pᵢ 的 Voronoi 区域定义为:
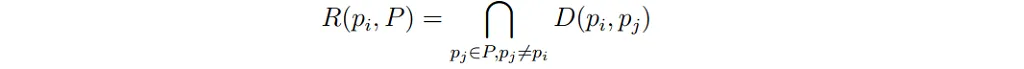
并且由到 pᵢ 的距离小于或等于到任何其他点 pⱼ ∈ P 的距离的所有点组成。一对 Voronoi 区域共享的边界称为 Voronoi 边。 Voronoi 边在 Voronoi 顶点相交。 P 的 Voronoi 图由下式给出:
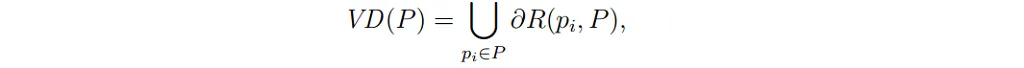
其中 ∂R(pᵢ,P) 表示 R(pᵢ,P) 的边界。术语有界 Voronoi 图是指 VD(P) 与其基础域的合取。
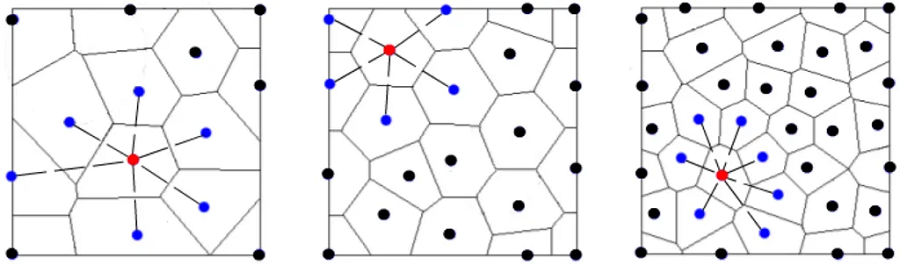
图 1:欧几里得平面中不同点集的 Voronoi 图以及它们强加在(红色)示例点上的(蓝色)所谓的自然邻域关系
我们将自己限制在欧几里得平面域中的点,例如,参见图 1。然而,Voronoi 图定义可以推广到在没有来自流形 M 的噪声的情况下获取的点 P,即 P ⊂ M 的更一般情况。例如,请参见图 2,了解 3D 流形上点的固有(非欧几里得)Voronoi 图。

类似地,我们没有定义关于距离函数 d 的距离度量:Voronoi 图定义适用于跨流形 M 定义的任何测地距离度量。因此,例如,在欧几里德平面域情况下,标准欧几里德距离函数可用于计算 d(⋅,⋅)。
点集 P = {p₁, p2, …, pₙ} ∈ ℝ² 的 Delaunay 三角剖分由 VD(P) 的对偶图给出,Delaunay 三角剖分的每条边都与 VD(P) 的一条边相关联,即 Delaunay 边连接 VD(P) 中的(自然)相邻点。请参见图 3 的示例。 Delaunay 三角剖分通常存在于欧几里得距离度量以外的度量中,但不能保证存在或明确定义。
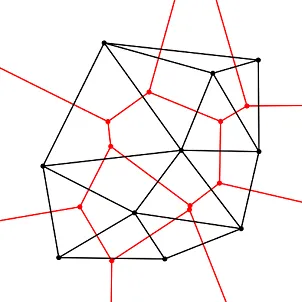
图 3:欧几里得平面中一组(黑色)点的(黑色)Delaunay 三角剖分及其对偶(红色)Voronoi 图(来源:维基百科)
我们参考 [1, 2],了解众多 Voronoi 图和 Delaunay 三角剖分变体(例如最远点和加权 Voronoi 图)的概述。出于我们的目的,我们可以将自己限制在它们的标准定义中。接下来我们看看他们的计算实现。
2、我们的实现
我们的实施基于以下核心要素:
- Python 3(在 Juypter Notebook 环境中使用)
- 适用于 Python 的 OpenCV 3.4.4.19 包装器包
为了确定面部标志,我们使用 Face++ 的演示功能。 使用你自己的示例图像使用此服务时,请考虑任何隐私问题。
如果你更喜欢基于 C++ 的实现,我们建议你查看 CGAL 及其 Voronoi 和 Delaunay 类。这些应该使以下 Python 编码“翻译”为 C++ 相当简单。 Python 编码的灵感来自 Satya Mallick 的博客文章,也可以在 GitHub 上找到。
除了 OpenCV 包之外,我们还使用 numpy 进行数组处理,使用 matplotlib 进行可视化:

辅助函数 rectContains 确定一个点是否落在矩形描述的图像域内,从而确定是否应将其视为图像 Delaunay 三角剖分的输入。
drawPoint 函数正是这样做的,即它在输入图像 img 上以彩色圆圈的形式显示面部标志 p。

voronoi函数使用subdiv成员函数getVoronoiFacetList来获取并随后根据输入图像img的初始OpenCV细分subdiv来绘制其Voronoi图。我们为 Voronoi 面可视化设置了随机配色方案。
类似地,delaunay函数在subdiv成员函数getTriangleList的帮助下确定并随后绘制输入图像img的初始Delaunay细分subdiv的三角形:


我们将这些函数应用于图 4 所示的示例图像。面部边界框和相应的面部标志由 Face++ 演示应用程序生成:

该演示服务返回一个 JSON 文件,其中包含服务在图像域内检测到的面部标志的 (x, y) 坐标等。上面显示了图 4 中输入图像的 JSON 提取。

图 4:原始样本图像(左)以及由 Face++ 生成的面部边界框(中)和相关的面部标志(右)
这些面部标志坐标代表 OpenCV 细分函数的输入点。我们通过使用标准 OpenCV imread 方法读取输入图像来开始展示生成。输入图像的矩形形状决定了存储在 rect 中的细分域。地标点以“Face2Points.txt”的形式上传到点数组中。然后,细分本身被实例化,并通过使用细分插入方法一一插入面部标志点来生成。
然后剩下要做的就是调用 delaunay 和 voronoi 函数传递输入图像及其新生成的细分。结果如图 5 所示:

图 5:输入图像的 Delaunay 三角剖分(左)及其对偶 Voronoi 图(右)
图 6 中的动画演示了输入图像一次一个面部标志点的 Delaunay 三角测量过程:

图 6:输入图像的 Delaunay 三角剖分动画
OpenCV subdiv 对象提供了各种用于检索 Delaunay 或 Voronoi 边和顶点的成员函数。详细信息我们参考OpenCV标准文档。这样,这些相当通用的几何结构的各种元素可以轻松地传递到后续图像处理或计算机视觉应用,例如面部分割、识别 [4,5,6] 和变形。
尽管我们在这篇博文中重点关注计算机视觉应用,但请注意,这些几何结构存在大量用例,其范围远远超出了计算机视觉领域,特别包括机器人导航等应用人工智能的其他领域。例如,请参阅[1,2]以获取灵感。
3、参考文献
[1] M. de Berg, O. Cheong, M. van Kreveld, and M. Overmars, Computational Geometry: Algorithms and Applications, 3rd edition, Springer, Berlin, Germany, 2010
[2] F. Aurenhammer, Voronoi Diagrams - A Survey of a Fundamental Geometric Data Structure, ACM Computing Surveys, 23(3), 1991, pp. 345–405
[3] R. Szeliski, Computer Vision: Algorithms and Applications, Springer, London, UK, 2011
[4] A. Cheddad, D. Mohamad, and A. A. Manaf, Exploiting Voronoi diagram properties in face segmentation and feature extraction, Pattern Recognition, Vol. 41, 2008, pp. 3842–3859
[5] M. A. Suhail, M. S. Obaidat, S. S. Ipson, and B. Sadoun, Content-based image segmentation, IEEE Int. Conf. Man Cybern. (SMC), Vol. 5, 2002
[6] M. Burge and W. Burger, Ear biometrics, in: A. Jain, R. Bolle, and S. Pankanti (eds.), Biometrics: Personal Identification in Networked Society, Kluwer Academic, Boston, MA, USA, 1999, pp. 273–285
原文链接:计算几何的机器视觉应用 - BimAnt
:JAVA面向对象特征性实验)



二次创新 | 微软新作StarNet:超强轻量级Backbone CVPR 2024)





机制)






:回溯算法——组合问题的优化(剪枝))

)