前言:
本系列是学习了董晓老师所讲的知识点做的笔记
董晓算法的个人空间-董晓算法个人主页-哔哩哔哩视频 (bilibili.com)
动态规划系列(还没学完)
【董晓算法】动态规划之线性DP问题-CSDN博客
【董晓算法】动态规划之背包DP问题(2024.5.11)-CSDN博客
【董晓算法】动态规划之背包DP与树形DP-CSDN博客
字符串系列
【董晓算法】竞赛常用知识之字符串1-CSDN博客
字典树
作用:
快速插入和查询字符串
插入
儿子数组 ch[p][j] 存储从节点 p沿着j这条边走到的子节点。
边为26个小写字母(a-z)对应的映射值0-25.
每个节点最多可以有26个分叉。例如,ch[0][2]=1,ch[1][0]=2.ch[2][19]=3。计数数组 cnt[p]存储以节点 p结尾的单词的插入次数
节点编号 idx 用来给节点编号
1.空 Trie 仅有一个根节点,编号为0。
枚举字符串的每个字符2,从根开始插,如果有儿子,则p指针走到儿子.
如果没儿子,则 先创建儿子,p指针再走到儿子
3、在单词结束点记录插入次数。
char s[N];
int ch[N][26], cnt[N], idx;
void insert(char* s)
{int p = 0;for (int i = 0; s[i]; i++) {int j = s[i] - 'a';if (!ch[p][j]) ch[p][j] = ++idx;p = ch[p][j];}cnt[p]++;
}
int query(char* s) {int p = 0;for (int i = 0; s[i]; i++) {int j = s[i] - 'a';if (!ch[p][j]) return 0;p = ch[p][j];}return cnt[p];
}查询和插入最主要的就是if (!ch[p][j]) 后不一样,和查询会返回值
最大异或对
任选两个进行异或运算,得到的结果最大是多少
思路:尽可能走相反位,结果最优(从根到叶的每一条路径都表示一个整数)
const int N = 100010;
int n, a[N];
int ch[N * 31][2], idx;//题目是2的23次void insert(int x) {int p = 0;for (int i = 30; i >= 0; i--) {int j = x >> i & 1; //取出第i位if (!ch[p][j])ch[p][j] = ++idx;p = ch[p][j];}
}
int query(int x) {int p = 0, res = 0;for (int i = 30; i >= 0; i--) {int j = x >> i & 1; //取出第i位if (ch[p][!j]) {res += 1 << i; //累加位权p = ch[p][!j];}else p = ch[p][j];}return res;
}
int main() {cin >> n;for (int i = 1; i <= n; i++)cin >> a[i], insert(a[i]);int ans = 0;for (int i = 1; i <= n; i++)ans = max(ans, query(a[i]));cout << ans;return 0;
}
int query(int x) {
int p = 0, res = 0;
for (int i = 30; i >= 0; i--) {
int j = x >> i & 1; //取出第i位
if (ch[p][!j]) {
res += 1 << i; //累加位权
p = ch[p][!j];
}
else p = ch[p][j];
}
return res;
}
AC自动机
AC 自动机(简单版) - 洛谷 (luogu.com.cn)
AC自动机是多模式匹配算法。给定 n个模式串和一个主串,查找有多少个模式串在主串中出现过
步骤
1.构造 Trie 树
先用n个模式串构造一颗Trie 。
Trie 中的一个节点表示一个从根到当前节点的字符串。
根节点表示空串,节点(5表示“s”,节点6表示“sh",节点7表示“she”。
如果节点是个模式串,则打个标记。例如,cnt[7]=1。
2.构造 AC自动机在 Trie 上构建两类边:回跳边和转移边3.扫描主串匹配
回跳边指向父节点的回跳边所指节点的儿子,从一个节点指向其最长后缀匹配节点
转移边指向当前节点的回跳边所指节点的儿子,从一个节点指向其直接子节点的链接

构树代码就是上面字典树的代码
构造 AC自动机
void build() {//建AC自动机queue<int> q;for (int i = 0; i < 26; i++)if (ch[0][i])q.push(ch[0][i]);while (q.size()) {int u = q.front(); q.pop();for (int i = 0; i < 26; i++) {int v = ch[u][i];if (v)ne[v] = ch[ne[u]][i], q.push(v);else ch[u][i] = ch[ne[u]][i];}}
}查找单词出现次数
扫描主串,依次取出字符 s[k].
1.i指针走主串对应的节点,沿着树边或转移边走保证不回退。
2.j指针沿着回跳边搜索模式串,每次从当前节点走到根节点,把当前节点中的所有后缀模式串一网打尽,保证不漏解。
3.扫描完主串,返回答案。
int query(char *s){int ans=0;for(int k=0,i=0;s[k];k++){i=ch[i][s[k]-'a'];for(int j=i;j&&~cnt[j];j=ne[j])//~cnt[i]检查cnt是不是-1ans+=cnt[j], cnt[j]=-1;}return ans;
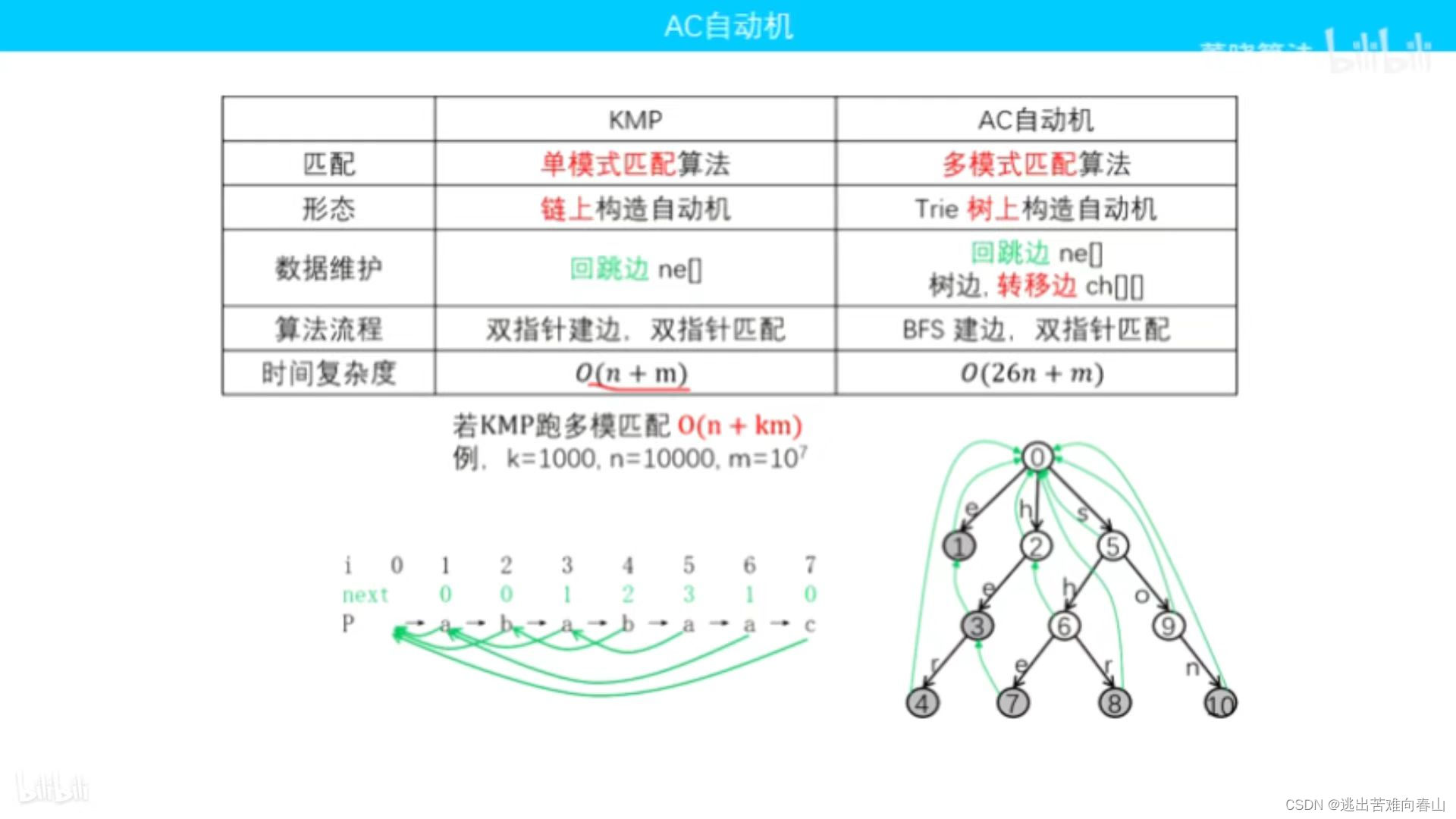
}KMP和AC自动机对比


)



和单星号(*)在Python参数传递中的妙用)


)

)

)





6)