伽马分布
关键词:Gamma Distribution
文章目录
- 一、说明
- 二、Gamma 分布的基础概念
- 2.1 Gamma 分布的物理意义
- 2.2 对比泊松与伽马分布
- 2.3 伽马分布参数
- 三、具有伽马分布的高效牙科调度
- 四、后记
一、说明
在本文中,我们将探讨统计学中的基本概率分布之一“伽马分布”。我们将揭示它在连续随机变量建模中的重要性,并将其与泊松分布进行对比。通过了解其参数,例如形状和速率,并深入研究实际示例,例如预测患者到达牙科诊所。
二、Gamma 分布的基础概念
2.1 Gamma 分布的物理意义
Gamma 分布的核心是表示事件发生之前的时间概率,例如等待时间或某些产品的使用寿命。它由两个参数控制:形状 ( α) 和速率 ( β),它们分别影响其形状和比例。这里务必不要与泊松分布混淆。
2.2 对比泊松与伽马分布
离散随机变量与连续随机变量:泊松分布对固定时间间隔内发生的事件数进行建模,给定事件发生的平均速率(例如:到达的客户数量)。另一方面,Gamma 分布的目的是对连续随机变量进行建模,表示非负实数(例如等待时间、生存时间…
参数: 泊松分布由单个参数定义,通常表示为 lambda λ(表示事件的平均发生率)。伽马分布由两个参数定义:形状 ( α) 和速率 ( β)
2.3 伽马分布参数
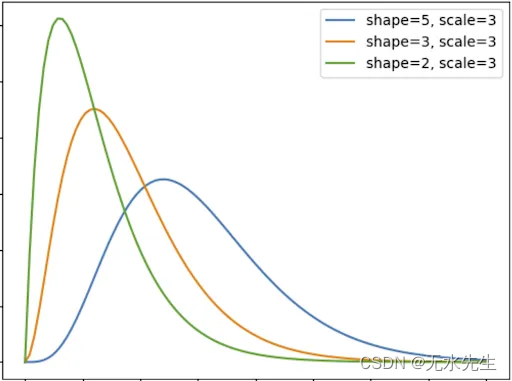
伽马分布。图片来源:builtin/data-science/gamma-distribution
1/ 形状参数 Alpha:shape 参数描述分布描述的事件数
2/ 比例参数 Beta:比例参数描述我们正在建模的事件之间的时间间隔。
3/ 累积分配函数 (CDF): Gamma 分布的 CDF 给出了随机变量 X 小于或等于某个值 x 的概率。它表示为 F(x),计算公式为:
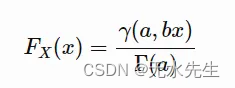
伽马分布中的累积分布函数 (CDF)。图片来源:
瓦利德·苏拉博士
γ(α,βx) 是较低的不完全伽马函数。
Γ(α) 是 gamma 函数。
4/ PDF格式:
Gamma 分布的概率密度函数 (PDF) 由下式给出:
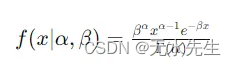
x 是随机变量。
α 和 β 是形状和速率参数。
Γ(α) 是 gamma 函数。
5/ 期望值

6/ 方差
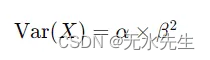
三、具有伽马分布的高效牙科调度
考虑牙科诊所的真实场景。患者根据泊松过程到达牙科诊所(这意味着患者的到达是相互独立的,并且随着时间的推移随机发生,没有任何固定模式或定期间隔),平均每小时 15 次。
让我们先计算一下前 10 位客户到达不到 3 分钟的概率!(我们可以使用伽马分布,因为我们正在对泊松过程中的等待时间进行建模)
在这种情况下:
形状参数 (α) (到达次数) 它是 3。
比例参数 (β) 为 60/15 或 (1/15)*60
import scipy.stats as statsalpha = 3
beta = 60/15 # Average time between arrivals (minutes)
time_until_3_customers = 10 #time until the arrival of the first 3 customers (in minutes)# Calculate the probability using the gamma CDF
probability_less_than_10_minutes = stats.gamma.cdf(time_until_3_customers, a=alpha, scale=beta)print("Probability that it takes less than 10 minutes for the first 3 customers to arrive:", probability_less_than_10_minutes)
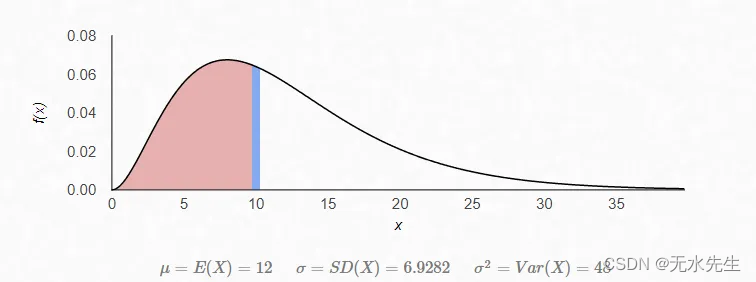
前 3 位客户到达所需时间少于 10 分钟的概率:0.4561
在 3 位客户到达牙科诊所之前,平均需要多长时间?
mean = alpha*beta
mean #12
距离第三位客户到达的平均时间为 12 分钟。
注意:如果你不想使用 Python,你可以在这里进行计算,也有很好的数据可视化: https://homepage.divms.uiowa.edu/~mbognar/applets/gamma.html
四、后记
当我们结束本文时,很明显,了解 Gamma 分布是预测事件随时间变化的关键。我们已经看到了它与泊松分布的不同之处,以及它在现实生活中的应用,例如预测患者到达牙医办公室的情况。但这里有一个想法值得深思!我们如何利用这些知识来进一步改进日常流程?







17.1-17.2)


)



)




