
问题分析
看到这个问题的同学很容易想到用十层循环暴力计算,反正是道填空题,一直算总能算得出来的,还有些同学可能觉得十层循环太恐怖了,写成回溯更简洁一点。像下面这样
#include <bits/stdc++.h>
using namespace std;
int cnt=0;
vector<bool> used(2023,false);
void dfs(int now,int len,int start) {if(len==10){if(now==2022){cnt++;}return;}for(int i=start;i<=2022-now;i++){if(!used[i]){used[i]=true;dfs(now+i,len+1,i+1);used[i]=false;}}
}
int main() {dfs(0,0,1);cout<<cnt<<endl;return 0;
}
但是我们分析一下,这个时间复杂度大概是 O ( C 2022 10 ) O(C_{2022}^{10}) O(C202210)级别的,这个数字太恐怖了,要高于 1 0 30 10^{30} 1030的数量级,而c++代码在平台上运行的速度大概是 1 0 9 10^{9} 109次每秒。所以,根本不可能暴力求出答案。而回溯不可以,我们可以动态规划嘛。这实际上就是典型的限量背包问题(如果不知道什么是限量背包问题,可以看我的这篇博客)。从物品(1~2022)中挑选10个物品,要求每种物品只能选一次,然后装满该背包(容量2022)有多少种组合?将该问题转化为背包问题就很容易解决了。(不过要记得用long long,这个数字很大)
具体代码如下
#include<iostream>
using namespace std;
long long int f[11][2023]= {0}; //f[j][k]:选择了j个物品满载容积k的背包的组合数
int i, j, k;
int main() {f[0][0]=1;for(i=1; i<=2022; i++) {//遍历每个物品 for(k=2022; k>=i; k--) {//遍历背包容量,从后往前遍历 for(j=1; j<=10; j++) {//遍历每个选择数量 f[j][k]+=f[j-1][k-i];}}}cout << f[10][2022];return 0;
}
结果
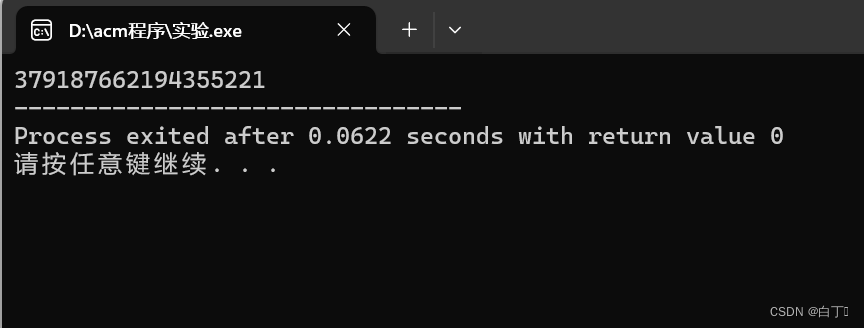



)





--8)
)



)




