70. 爬楼梯 （进阶）

思路：

我们之前做的 爬楼梯 是只能至多爬两个台阶。

这次改为：一步一个台阶，两个台阶，三个台阶，.......，直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢？

这又有难度了，这其实是一个完全背包问题。

1阶，2阶，.... m阶就是物品，楼顶就是背包。

每一阶可以重复使用，例如跳了1阶，还可以继续跳1阶。

问跳到楼顶有几种方法其实就是问装满背包有几种方法。

此时大家应该发现这就是一个完全背包问题了！

动规五部曲分析如下：

1.确定dp数组以及下标的含义

dp[i]：爬到有i个台阶的楼顶，有dp[i]种方法。

2.确定递推公式

在动态规划：494.目标和 (opens new window)、 动态规划：518.零钱兑换II (opens new window)、动态规划：377. 组合总和 Ⅳ (opens new window)中我们都讲过了，求装满背包有几种方法，递推公式一般都是dp[i] += dp[i - nums[j]];

本题呢，dp[i]有几种来源，dp[i - 1]，dp[i - 2]，dp[i - 3] 等等，即：dp[i - j]

那么递推公式为：dp[i] += dp[i - j]

3.dp数组如何初始化

既然递归公式是 dp[i] += dp[i - j]，那么dp[0] 一定为1，dp[0]是递归中一切数值的基础所在，如果dp[0]是0的话，其他数值都是0了。

下标非0的dp[i]初始化为0，因为dp[i]是靠dp[i-j]累计上来的，dp[i]本身为0这样才不会影响结果

4.确定遍历顺序

这是背包里求排列问题，即：1、2 步 和 2、1 步都是上三个台阶，但是这两种方法不一样！（求排列）

所以需将target放在外循环，将nums放在内循环。

每一步可以走多次，这是完全背包，内循环需要从前向后遍历。

5.举例来推导dp数组

介于本题和动态规划：377. 组合总和 Ⅳ (opens new window)几乎是一样的，这里我就不再重复举例了。

代码：

def climbing_stairs(n,m):dp = [0]*(n+1) # 背包总容量dp[0] = 1 # 排列题，注意循环顺序，背包在外物品在内for j in range(1,n+1):for i in range(1,m+1):if j>=i:dp[j] += dp[j-i] # 这里i就是重量而非indexreturn dp[n]if __name__ == '__main__':n,m = map(int,input().split())print(climbing_stairs(n,m))

• 时间复杂度: O(n * m)，代码中m表示最多可以爬m个台阶，代码中把m改成2就是力扣：70.爬楼梯的解题思路。
• 空间复杂度: O(n)

补充：

提到拆分就不能不提split()，input输入多个内容默认会被定义为一个序列，所以也处于split()的拆分范畴内。

Str.split(str,num)

"Str"表示需要拆分的字符串；
split()中有两个参数，“str”表示分隔符，num则表示需要拆分的次数。
如果不传入实际参数，则默认str的值为空格、制表符，num的默认值为-1，即能够拆分的所有次数
下面进行实际演示：

str="my name is undefineing"
i1,i2,i3,i4=str.split()
print(i1)
print(i2)
print(i3)
print(i4)

map函数，map()函数会根据提供的对指定的可迭代对象可迭代对象的每个元素进行运算，并将返回运算结果的迭代器。

map(function,str)

这里的map有两个参数，其中function为一个函数，str则为一个可迭代对象，将str中的元素送入function函数中进行加工，来达到自己想要的效果。 

input().split（）拆分后默认是一个字符列表，而int是强制类型转换的函数，换成float之类的也行，将这个字符列表送入int函数中加工，最后得到的就是的数值列表，再通过切片赋值给i1,i2,i3等几个变量就达到了拆分input输入内容的同时并转换类型的目的。

i1,i2,i3=map(int,input("请输入三个数：").split(","))
print(i1," ",i2," ",i3)

​ 

在python中，只要是序列，都可以这样赋值。

a, b, c, d = ("shell","perl","php","python")
a, b, c, d = ["shell","perl","php","python"]

但是变量和序列中的元素必须一一对应。如果变量名与元素个数不同，则会报错，除非只有一个变量名，这表示将整个序列赋值给这个变量。 

322. 零钱兑换

思路：

在动态规划：518.零钱兑换II (opens new window)中我们已经兑换一次零钱了，这次又要兑换，套路不一样！

题目中说每种硬币的数量是无限的，可以看出是典型的完全背包问题。

动规五部曲分析如下：

1.确定dp数组以及下标的含义

dp[j]：凑足总额为j所需钱币的最少个数为dp[j]

2.确定递推公式

凑足总额为j - coins[i]的最少个数为dp[j - coins[i]]，那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j]（考虑coins[i]）

所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。

递推公式：dp[j] = min(dp[j - coins[i]] + 1, dp[j]); （在这里min中的dp[j - coins[i]] + 1表示放coin[i]，dp[j]表示不放）

3.dp数组如何初始化

首先凑足总金额为0所需钱币的个数一定是0，那么dp[0] = 0;

其他下标对应的数值呢？

考虑到递推公式的特性，dp[j]必须初始化为一个最大的数，否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。（防止递推公式的值被初始值覆盖）

所以下标非0的元素都是应该是最大值。

4.确定遍历顺序

本题求钱币最小个数，那么钱币有顺序和没有顺序都可以，都不影响钱币的最小个数。

所以本题并不强调集合是组合还是排列。

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

在动态规划专题我们讲过了求组合数是动态规划：518.零钱兑换II (opens new window)，求排列数是可迭代对象。

所以本题的两个for循环的关系是：外层for循环遍历物品，内层for遍历背包或者外层for遍历背包，内层for循环遍历物品都是可以的！

那么我采用coins放在外循环，target在内循环的方式。

本题钱币数量可以无限使用，那么是完全背包。所以遍历的内循环是正序

综上所述，遍历顺序为：coins（物品）放在外循环，target（背包）在内循环。且内循环正序。

5.举例推导dp数组

以输入：coins = [1, 2, 5], amount = 5为例

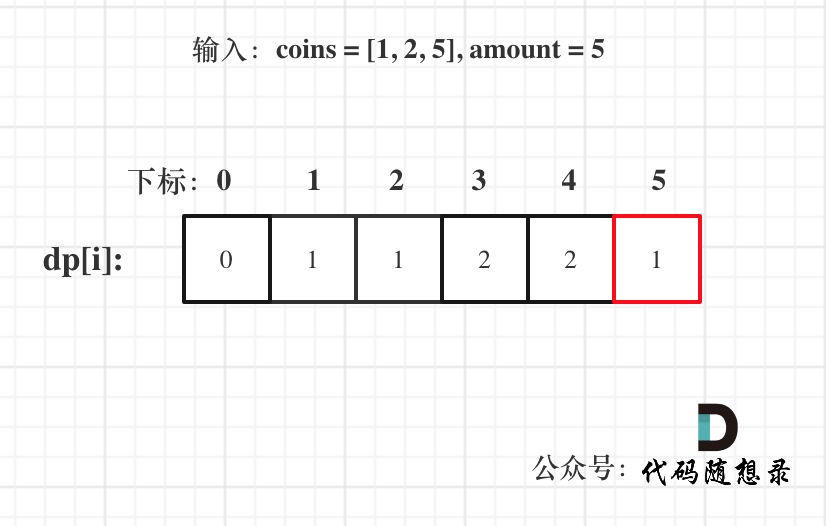
dp[amount]为最终结果。

代码：

class Solution:def coinChange(self, coins: List[int], amount: int) -> int:dp = [float('inf')] * (amount + 1)  # 创建动态规划数组，初始值为正无穷大dp[0] = 0  # 初始化背包容量为0时的最小硬币数量为0for coin in coins:  # 遍历硬币列表，相当于遍历物品for i in range(coin, amount + 1):  # 遍历背包容量#if i - coin != float("inf"):  # 如果dp[i - coin]不是初始值，则进行状态转移(这句不要也行)dp[i] = min(dp[i - coin] + 1, dp[i])  # 更新最小硬币数量if dp[amount] == float('inf'):  # 如果最终背包容量的最小硬币数量仍为正无穷大，表示无解return -1return dp[amount]  # 返回背包容量为amount时的最小硬币数量

• 时间复杂度: O(n * amount)，其中 n 为 coins 的长度
• 空间复杂度: O(amount)

279. 完全平方数

思路：

可能刚看这种题感觉没啥思路，又平方和的，又最小数的。

我来把题目翻译一下：完全平方数就是物品（可以无限件使用），凑个正整数n就是背包，问凑满这个背包最少有多少物品？

感受出来了没，这么浓厚的完全背包氛围，而且和昨天的题目动态规划：322. 零钱兑换 (opens new window)就是一样一样的！

动规五部曲分析如下：

 1.确定dp数组（dp table）以及下标的含义

dp[j]：和为j的完全平方数的最少数量为dp[j]

 2.确定递推公式

dp[j] 可以由dp[j - i * i]推出， dp[j - i * i] + 1 便可以凑成dp[j]。

此时我们要选择最小的dp[j]，所以递推公式：dp[j] = min(dp[j - i * i] + 1, dp[j]);

 3.dp数组如何初始化

dp[0]表示 和为0的完全平方数的最小数量，那么dp[0]一定是0。

非0下标的dp[j]应该是多少呢？

从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的，所以非0下标的dp[j]一定要初始为最大值，这样dp[j]在递推的时候才不会被初始值覆盖。

 4.确定遍历顺序

我们知道这是完全背包，

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

在动态规划：322. 零钱兑换 (opens new window)中我们就深入探讨了这个问题，本题也是一样的，是求最小数！

所以本题外层for遍历背包，内层for遍历物品，还是外层for遍历物品，内层for遍历背包，都是可以的！

 5.举例推导dp数组

已输入n为5例，dp状态图如下：

最后的dp[n]为最终结果。

代码：

class Solution:def numSquares(self, n: int) -> int:cur=[]i=1while i**2<=n: # 生成小于等于n的所有平方数cur.append(i**2)i+=1res=[float('inf')] * (n + 1)res[0]=0for x in cur:for i in range(x,n+1):res[i]=min(res[i],res[i-x]+1)return res[-1]

• 时间复杂度: O(n * √n)
• 空间复杂度: O(n)