引言

关于这个单源最短路的综合应用，其实最短路问题最简单的就是模板了，这是一个基础，然后会与各种算法结合到一块，就是不再考察单个知识点了，而是各种知识点融合到一块，你一块地方不会，你这道题就做不出来，主要是跟二分、暴搜等算法结合。

---

一、新年好

标签：单源最短路、枚举

思路：这道题给了一个无向图，然后问从一个起点出发，中途必须至少经过 $5$ 个点，问最短的路径是什么。思路就是我们可以暴力枚举这 $5$ 个点的顺序，然后经过每一个点肯定是一个最短路，所以我们可以提前预处理出来算上起点在内的 $6$ 个点到每一个点的最短路，然后暴力枚举经过点的顺序，然后求其路径和的最小值即可，详情见代码。

题目描述：

重庆城里有 n 个车站，m 条 双向 公路连接其中的某些车站。每两个车站最多用一条公路连接，从任何一个车站出发都可以经过一条或者多条公路到达其他车站，但不同的路径需要花费的时
间可能不同。在一条路径上花费的时间等于路径上所有公路需要的时间之和。佳佳的家在车站 1，他有五个亲戚，分别住在车站 a,b,c,d,e。过年了，他需要从自己的家出发，拜访每个亲戚（顺序任意），给他们送去节日的祝福。怎样走，才需要最少的时间？输入格式
第一行：包含两个整数 n,m，分别表示车站数目和公路数目。第二行：包含五个整数 a,b,c,d,e，分别表示五个亲戚所在车站编号。以下 m 行，每行三个整数 x,y,t，表示公路连接的两个车站编号和时间。输出格式
输出仅一行，包含一个整数 T，表示最少的总时间。数据范围
1≤n≤50000,1≤m≤105,1<a,b,c,d,e≤n,1≤x,y≤n,1≤t≤100
输入样例：
6 6
2 3 4 5 6
1 2 8
2 3 3
3 4 4
4 5 5
5 6 2
1 6 7
输出样例：
21

示例代码：

#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 5e4+10, M = 2e5+10, INF = 0x3f3f3f3f;int n, m;
int h[N], e[M], w[M], ne[M], idx;
int dist[6][N];
bool st[N];
int path[6] = {1};void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}void dijkstra(int s, int dist[])
{memset(dist, 0x3f, N * 4);memset(st, 0, sizeof st);dist[s] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;heap.push({0,s});while(heap.size()){auto t = heap.top(); heap.pop();int p = t.y;if(st[p]) continue;st[p] = true;for(int i = h[p]; i != -1; i = ne[i]){int j = e[i];if(dist[j] > dist[p] + w[i]){dist[j] = dist[p] + w[i];heap.push({dist[j],j});}}}
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);memset(h, -1, sizeof h);cin >> n >> m;for(int i = 1; i < 6; ++i) cin >> path[i];while(m--){int a, b, c; cin >> a >> b >> c;add(a,b,c), add(b,a,c);}for(int i = 0; i < 6; ++i) dijkstra(path[i], dist[i]);LL res = 1e18;int arr[5] = {1,2,3,4,5};do{int last = 0;LL sum = 0;for(int i = 0; i < 5; ++i){int j = arr[i];sum += dist[last][path[j]];last = j;}res = min(res, sum);}while(next_permutation(arr,arr+5));cout << res << endl;return 0;
}

---

二、通信线路

标签：图论、SPFA、动态规划、二分、双端队列BFS

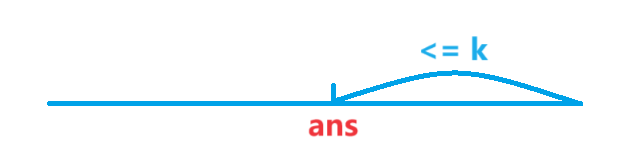
思路：首先这道题可以简化为求第 $k+1$ 大的路径中的最小值，最值的问题我们一半可以用二分来做。首先就是要找到一个性质，假如我们已经找到了答案，如下图，那么答案右边的区间中的边权 $\ge ans$ 的肯定是 $\le k$ 的。然后我们就用二分去做，我们可以建立一个图，大于 $ans$ 的边权为 $1$ ，反之为 $0$ ，然后我们可以用最短算法即可。值得注意的是二分的边界点问题，左边界肯定是 $0$ ，因为有可能最少路径数是小于等于 $k$ 的，然后最大可能为 $1e6$ ，但是这道题还可能出现路径不存在的情况，根据性质二分会逼近右端点，这时将无法判断，所以我们可以将右端点取 $1e6+1$ 这样合法的最大值为 $1e6$ ，但要是不存在路径，则为右端点。另外只有 $01$ 的边权的最短路可以用双端队列 $BFS$ 来做，其实就是一个简易版的堆优化版的 $Dijkstra$ 。

题目描述：

在郊区有 N 座通信基站，P 条 双向 电缆，第 i 条电缆连接基站 Ai 和 Bi。特别地，1 号基站是通信公司的总站，N 号基站位于一座农场中。现在，农场主希望对通信线路进行升级，其中升级第 i 条电缆需要花费 Li。电话公司正在举行优惠活动。农产主可以指定一条从 1 号基站到 N 号基站的路径，并指定路径上不超过 K 条电缆，由电话公司免费提供升级服务。农场主只需要支付在该路径上剩余的电缆中，升级价格最贵的那条电缆的花费即可。求至少用多少钱可以完成升级。输入格式
第 1 行：三个整数 N，P，K。第 2..P+1 行：第 i+1 行包含三个整数 Ai,Bi,Li。输出格式
包含一个整数表示最少花费。若 1 号基站与 N 号基站之间不存在路径，则输出 −1。数据范围
0≤K<N≤1000,1≤P≤10000,1≤Li≤1000000
输入样例：
5 7 1
1 2 5
3 1 4
2 4 8
3 2 3
5 2 9
3 4 7
4 5 6
输出样例：
4

示例代码：

#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1010, M = 2e4+10, INF = 0x3f3f3f3f;int n, p, k;
int h[N], e[M], w[M], ne[M], idx;
deque<int> q;
int dist[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}bool check(int bound)
{memset(dist, 0x3f, sizeof dist);memset(st, 0, sizeof st);dist[1] = 0;q.push_back(1);while(q.size()){int t = q.front(); q.pop_front();if(st[t]) continue;st[t] = true;for(int i = h[t]; i != -1; i = ne[i]){int j = e[i], v = w[i] > bound;if(dist[j] > dist[t] + v){dist[j] = dist[t] + v;if(!v) q.push_front(j);else q.push_back(j);}}}return dist[n] <= k;
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);memset(h, -1, sizeof h);cin >> n >> p >> k;while(p--){int a, b, c; cin >> a >> b >> c;add(a,b,c), add(b,a,c);}int l = 0, r = 1e6+1;while(l < r){int mid = l + r >> 1;if(check(mid)) r = mid;else l = mid + 1;}if(r == 1e6+1) r = -1;cout << r << endl;return 0;
}

---

三、道路与航线

标签：图论、Dijkstra、最短路

思路：这道题一看带有负权边，那就可以拿 $spfa$ 直接做了，建图的方式也是很常规，然后就是数据比较大，所以有几个样例过不了，其实对于打蓝桥杯其实是够了的，因为大部分分拿到手就够了，要看目的是什么。其实正确的写法应该是把陆地连一起，然后用拓扑序来做，可这样很费时间而且不好写，所以就不做了。但是要过全部数据可以拿 $LIS$ 进行优化，类似于双端队列广搜，具体细节见代码。

题目描述：

农夫约翰正在一个新的销售区域对他的牛奶销售方案进行调查。他想把牛奶送到 T 个城镇，编号为 1∼T。这些城镇之间通过 R 条道路 (编号为 1 到 R) 和 P 条航线 (编号为 1 到 P) 连接。每条道路 i 或者航线 i 连接城镇 Ai 到 Bi，花费为 Ci。对于道路，0≤Ci≤10,000;然而航线的花费很神奇，花费 Ci 可能是负数(−10,000≤Ci≤10,000)。道路是双向的，可以从 Ai 到 Bi，也可以从 Bi 到 Ai，花费都是 Ci。然而航线与之不同，只可以从 Ai 到 Bi。事实上，由于最近恐怖主义太嚣张，为了社会和谐，出台了一些政策：保证如果有一条航线可以从 Ai 到 Bi，那么保证不可能通
过一些道路和航线从 Bi 回到 Ai。由于约翰的奶牛世界公认十分给力，他需要运送奶牛到每一个城镇。他想找到从发送中心城镇 S 把奶牛送到每个城镇的最便宜的方案。输入格式
第一行包含四个整数 T,R,P,S。接下来 R 行，每行包含三个整数（表示一个道路）Ai,Bi,Ci。接下来 P 行，每行包含三个整数（表示一条航线）Ai,Bi,Ci。输出格式
第 1..T 行：第 i 行输出从 S 到达城镇 i 的最小花费，如果不存在，则输出 NO PATH。数据范围
1≤T≤25000,1≤R,P≤50000,1≤Ai,Bi,S≤T
输入样例：
6 3 3 4
1 2 5
3 4 5
5 6 10
3 5 -100
4 6 -100
1 3 -10
输出样例：
NO PATH
NO PATH
5
0
-95
-100

示例代码：

#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 3e5+10, M = 2e5+10, INF = 0x3f3f3f3f;int n, r, p, S;
int h[N], e[M], w[M], ne[M], idx;
int dist[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}void spfa()
{memset(dist, 0x3f, sizeof dist);dist[S] = 0, st[S] = true;deque<int> q; q.push_back(S);while(q.size()){int t = q.front(); q.pop_front();st[t] = false;for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];if(dist[j] > dist[t] + w[i]){dist[j] = dist[t] + w[i];if(!st[j]){if(q.size() && dist[j] < dist[q.front()]) q.push_front(j);else q.push_back(j);}}}}
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);memset(h, -1, sizeof h);cin >> n >> r >> p >> S;while(r--){int a, b, c; cin >> a >> b >> c;add(a,b,c), add(b,a,c);}while(p--){int a, b, c; cin >> a >> b >> c;add(a,b,c);}spfa();for(int i = 1; i <= n; ++i){int t = dist[i];if(t == INF) cout << "NO PATH" << endl;else cout << t << endl;}return 0;
}

---

四、最优贸易

标签：图论、SPFA

思路：首先这道题问的是最大的差价是什么，那么肯定存在一个分界点，使得这个点之前的最小值和这个点之后的最大值的差值最大，那么我们就可以找到每一个点之前的最小值和其之后的最大值，然后取它们差值的最大值即可。首先这道题不能用 $Dijkstra$ ，因为这个算法本质还是一个 $BFS$ 算法，就是每个点只会遍历一次，第一次遍历的为极值，但是这道题中你第一次走到的点不一定就是极值点，所以采用 $spfa$ 算法，然后将 $dist$ 数组改为 $dmin,dmax$ ，记录每个点之前的最值，然后最小值从前往后遍历，最大值从后向前遍历即可。

题目描述：

C 国有 n 个大城市和 m 条道路，每条道路连接这 n 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为 1 条。C 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。商人阿龙来到 C 国旅游。当他得知“同一种商品在不同城市的价格可能会不同”这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚一点
旅费。设 C 国 n 个城市的标号从 1∼n，阿龙决定从 1 号城市出发，并最终在 n 号城市结束自己的旅行。在旅游的过程中，任何城市可以被重复经过多次，但不要求经过所有 n 个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品——水晶球，并在之后经过的另一个城市卖出
这个水晶球，用赚取的差价当做旅费。因为阿龙主要是来 C 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。现在给出 n 个城市的水晶球价格，m 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。注意：本题数据有加强。输入格式
第一行包含 2 个正整数 n 和 m，中间用一个空格隔开，分别表示城市的数目和道路的数目。第二行 n 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 n 个城市的商品价格。接下来 m 行，每行有 3 个正整数，x，y，z，每两个整数之间用一个空格隔开。如果 z=1，表示这条道路是城市 x 到城市 y 之间的单向道路；如果 z=2，表示这条道路为城市 x 和城市 y 之间的双向道路。输出格式
一个整数，表示答案。数据范围
1≤n≤100000,1≤m≤500000,1≤各城市水晶球价格≤100
输入样例：
5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2
输出样例：
5

示例代码：

#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1e5+10, M = 2e6+10, INF = 0x3f3f3f3f;int n, m;
int w[N];
int hs[N], he[N], e[M], ne[M], idx;
int dmin[N], dmax[N];
bool st[N];void add(int h[], int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}void spfa(int S, int dist[], int h[], bool flag)
{memset(st, 0, sizeof st);if(flag) memset(dist, 0x3f, sizeof dmin);else memset(dist, -1, sizeof dmin);st[S] = true, dist[S] = w[S];queue<int> q; q.push(S);while(q.size()){int t = q.front(); q.pop();st[t] = false;for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];if((flag && dist[j] > min(dist[t],w[j])) || (!flag && dist[j] < max(dist[t],w[j]))){if(flag){dist[j] = min(dist[t], w[j]);}else{dist[j] = max(dist[t], w[j]);}if(!st[j]) st[j] = true, q.push(j);}}}
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);memset(hs, -1, sizeof hs);memset(he, -1, sizeof he);cin >> n >> m;for(int i = 1; i <= n; ++i) cin >> w[i];while(m--){int a, b, c; cin >> a >> b >> c;add(hs,a,b), add(he,b,a);if(c == 2) add(hs,b,a), add(he,a,b);}spfa(1,dmin,hs,true);spfa(n,dmax,he,false);int res = 0;for(int i = 1; i <= n; ++i){res = max(res, dmax[i] - dmin[i]);}cout << res << endl;return 0;
}