目录
1. 简介
2. 频谱相关参数
2.1 频谱相关基本概念
2.1.1 采样时间间隔
2.1.2 采样频率
2.1.3 采样点数
2.1.4 采样时间长度
2.1.5 谱线数
2.1.6 奈奎斯特频率
2.1.7 频谱分辨率
2.1.8 最高分析频率
2.1.9 频谱泄露
2.2 窗函数
2.2.1 AD2的窗函数
2.2.2 测试矩形窗
2.2.3 测试平顶窗
2.3 频谱参数
2.3.1 幅值单位解释
2.3.2 几个常量解释
2.3.3 动态指标
3. 其他相关知识
3.1 归一化
3.2 DFT 示例
4. 总结
1. 简介
通过AD2记录频谱相关知识。
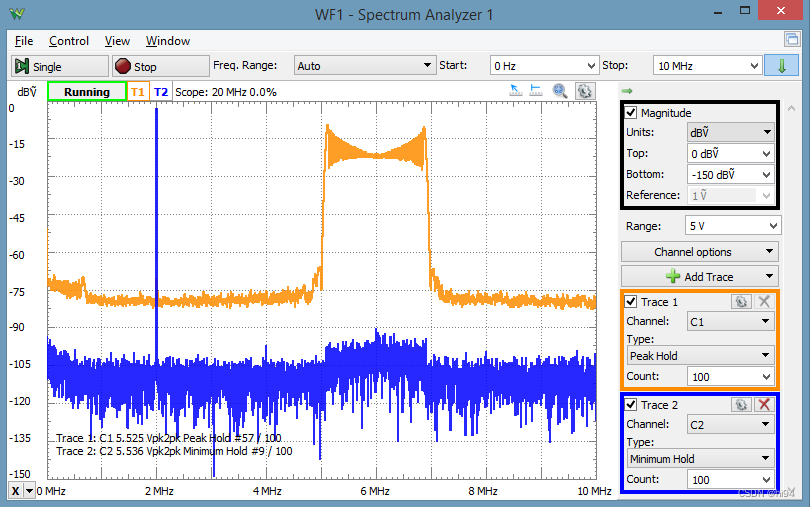
2. 频谱相关参数
2.1 频谱相关基本概念
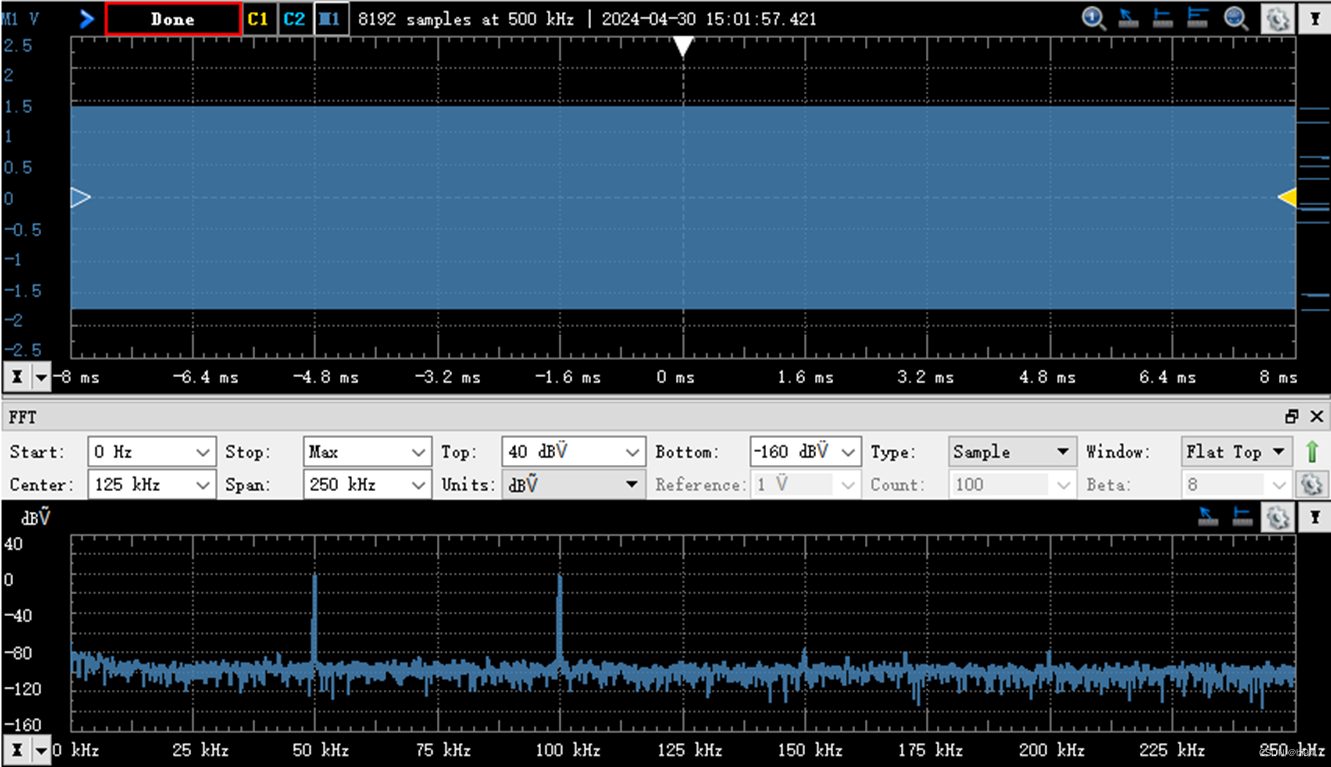
2.1.1 采样时间间隔
采样时间间隔,也称采样周期,一般使用 Ts 表示,Time sampling,是在数字信号处理中连续信号转换为离散信号时,连续信号的两次采样之间的时间差,用于说明多久采集一次信号的数据点。
截图中并未直接显示采样时间间隔,但可以通过采样频率500kHz换算,Ts=0.2ms。
2.1.2 采样频率
采样频率(fs)和采样时间间隔是描述数字信号采样过程的两个互为倒数的概念。尽管两者都能准确描述采样的属性,但在实际应用和理论讨论中,采样频率更为常用。
可能用采样频率更直观吧,而且还和奈奎斯特定理的关联,讨论采样频率而不是采样时间间隔,使得这一原则更易于理解和应用。
截图中直接显示了采样频率为500kHz。
2.1.3 采样点数
离散样本的总数。用N表示。
截图中显示的“8192 samples at 500kHz”中的“8192”就是采样点数。
2.1.4 采样时间长度
采样时间长度,用T表示。
2.1.5 谱线数
谱线数,在频谱图中出现的频率点数(不包含直流分量),用M表示。
2.1.6 奈奎斯特频率
由奈奎斯特采样定理(Nyquist Sampling Theorem)所确定,用fN表示。
2.1.7 频谱分辨率
频谱分辨率,,是指能够分辨两个相邻频率成分的最小频率间隔。
理论上,频谱分辨率由信号的采样时间长度决定,计算公式为:
T=1s,总采样时长1s, Δf=1Hz;
T=10s,总采样时长10s, Δf=0.1Hz;
2.1.8 最高分析频率
由奈奎斯特采样定理(Nyquist Sampling Theorem)所确定。用fmax表示。
2.1.9 频谱泄露
实际测量的信号是有限时长的,超出测量时长的信号就是未知的。当使用 FFT 算法(用于计算 DFT)对限时信号切片进行分析时,FFT 隐含地假设该信号在观察到的间隔后本质上会重复自身。这可能会导致每个切片边缘处的不连续性,从而导致每个测量时长的信号(Tn)中包含的能量溢出到其他测量时长的信号(Tm)频率谱中。这种现象称为频谱泄漏。
2.2 窗函数
窗函数用于在进行傅里叶变换之前修改信号,这些函数通过在信号的两端乘以特定的系数,即信号与窗函数相乘,以平滑 FFT 切片边缘的不连续性,从而减少边缘效应(频谱泄漏),改善频谱分析的结果。
2.2.1 AD2的窗函数
Digilent AD2提供以下窗函数:
- Rectangular(矩形窗): 所有数据点都有相同的权重,主瓣非常窄(理论上具有最高的频谱分辨率),但旁瓣较高,会导致频谱泄漏。
- Triangular(三角窗): 也称为Bartlett窗,中心点权重最大,向两端线性递减,旁瓣比矩形窗低,但主瓣更宽。
- Hamming(汉明窗): 提供加权的余弦形状,旁瓣水平比矩形窗低,主瓣宽度适中,适合处理频率相近的信号。
- Hann(ing)(汉宁窗): 类似汉明窗,但提供更平滑的加权,有助于进一步降低旁瓣水平。
- Cosine(余弦窗): 使用余弦波形加权数据,某些应用中可以提供良好的频率分辨率。
- Blackman-Harris(布莱克曼-哈里斯窗): 结合多个余弦项来减少旁瓣,最小化旁瓣水平时非常有效。
- Flat Top(平顶窗): 设计用来保持信号的幅度精度,中心附近平坦,适用于频谱分析中的幅度校准。
- Kaiser(凯撒窗): 由James Kaiser在贝尔实验室开发,是一种参数化的窗函数,用于有限冲激响应滤波器设计和频谱分析。Kaiser窗通过调整参数α(或β=πα),在主瓣宽度和旁瓣水平之间进行权衡。
2.2.2 测试矩形窗
输入为50kHz正弦,Window=Rectangular,可以看到在频谱图中50kHz的谱宽非常窄。
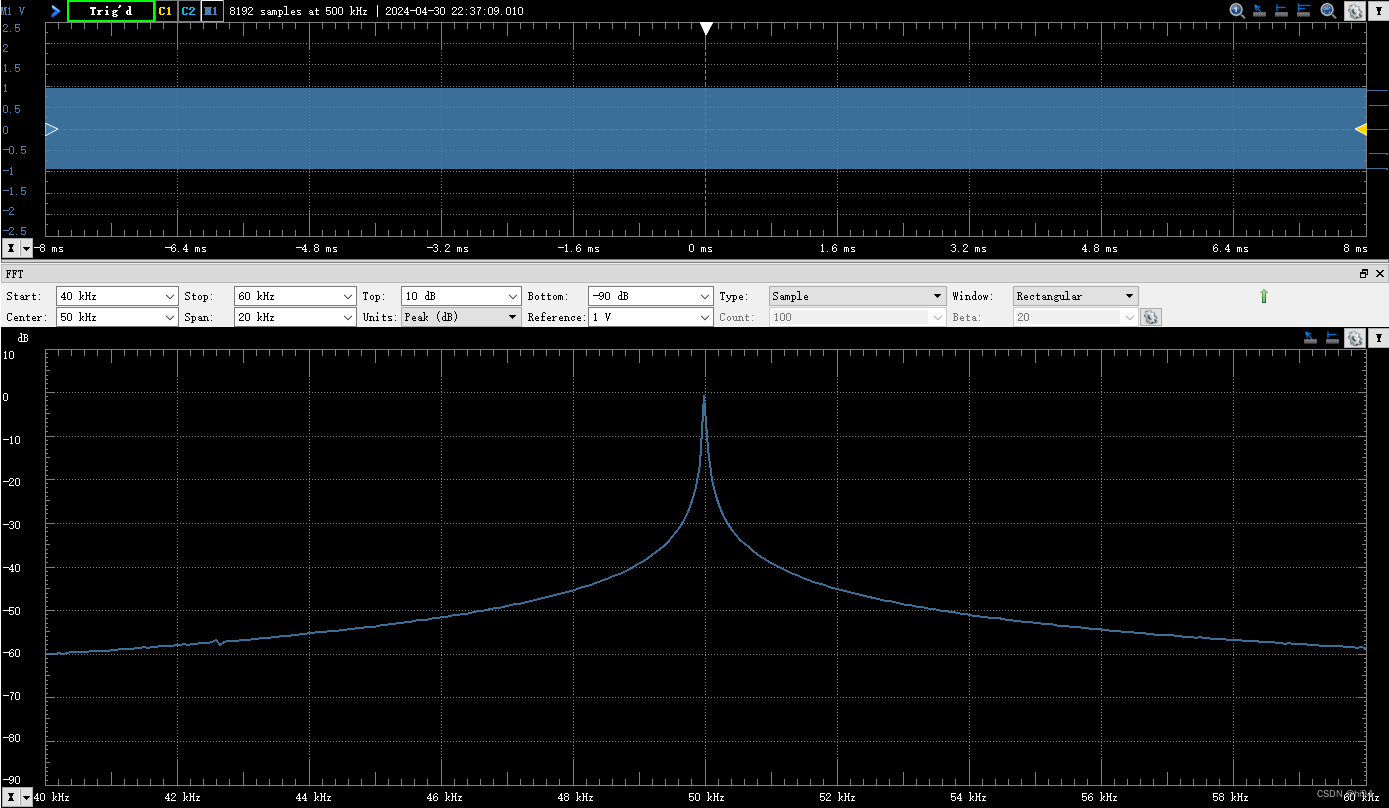
2.2.3 测试平顶窗
输入为50kHz正弦,Window=Flat Top,可以看到在频谱图中50kHz的谱宽有所增加,但是幅度值和Rectangular接近,Flat Top窗对幅值精度有较好的保留。
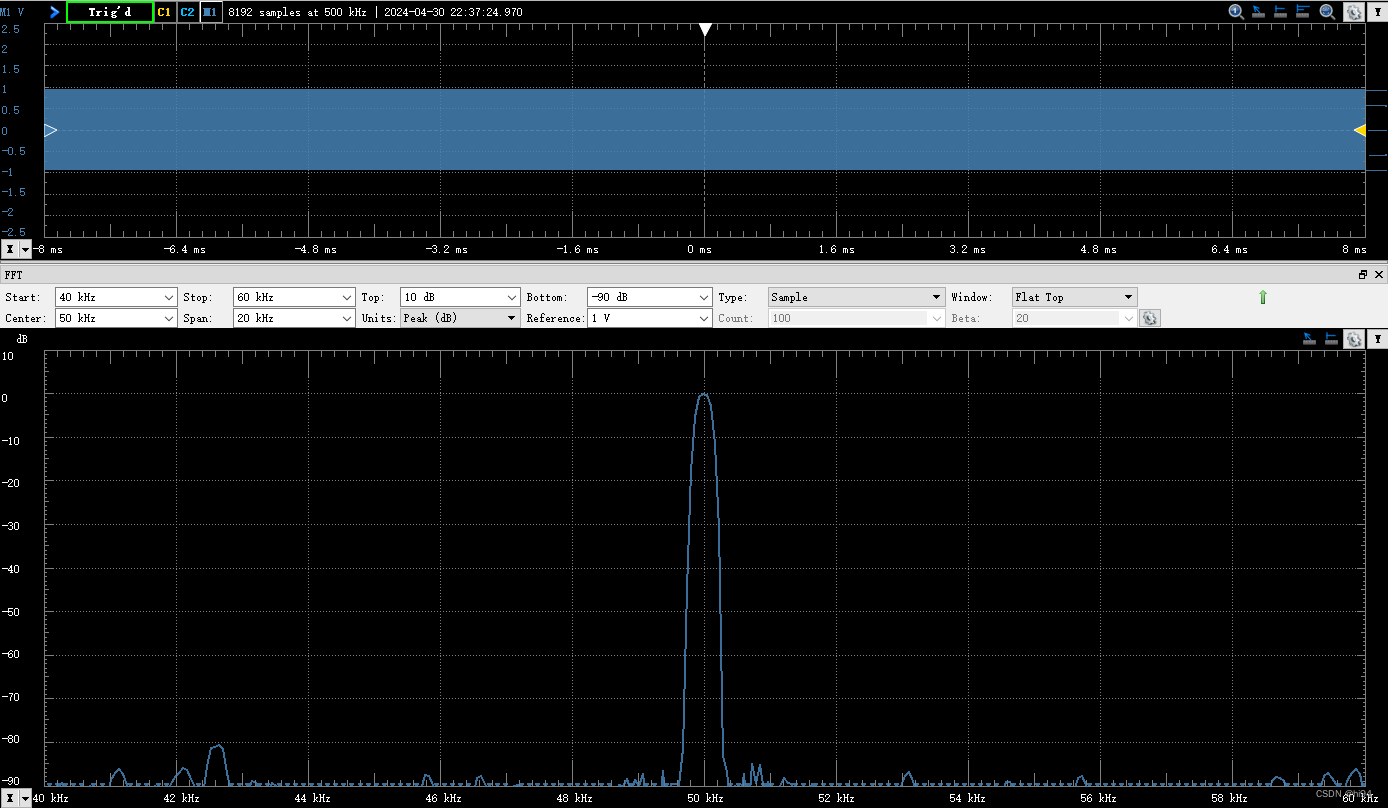
2.3 频谱参数
2.3.1 幅值单位解释

- 幅值的单位可以在图示位置设置
- 部分单位需要同时设置Reference
| Value | Unit | Description |
| 1.0037 V | Peak (V) | Relative to 1V amplitude sine wave. |
| 0.70973 Ṽ | RMS (Ṽ) | Relative to 1Ṽ (1.41V amplitude) sine wave. |
| 0.3308 VHz | Ṽ/√Hz (VHz) | is RMS value / square root (RBW). |
| 0.0322 dB | Peak (dB) | dB reference to peak value(sine wave). |
| -2.9781 dB | RMS (dB) | dB reference to RMS value. |
| -2.9781 dBṼ | dBṼ | dB reference to 1Ṽ sine wave, 20*Log10(Ṽ). |
| -0.7596 dBu | dBu | dB reference to 0.775Ṽ sine wave, 20*Log10(Ṽ/0.775). |
| 10.03 dBm | dBm | dB reference to 0.224Ṽ sine wave, relative to 1mW on 50Ω load. |
| 3.402 dBmHz | dBm/√Hz | dBm - 10*Log10(RBW/1Hz). |
| 63.4 dBmMHz | dBm/√MHz | dBm - 10*Log10(RBW/1MHz). |
| -8.8685 dBO | dBOV | dB reference to full scale square wave, 20*Log10Ṽ/VFSSquare). |
| -11.8788 dBFS | dBFS | dB reference to full scale sine wave, 20*Log10(Ṽ/VFSSine). |
2.3.2 几个常量解释

- ENBW: Normalized equivalent noise bandwidth of window function,窗函数的归一化等效噪声带宽。该参数由窗函数决定。详细计算过程见:Equivalent noise bandwidth (ENBW) of window functions - GaussianWaves
- Resolution: Resolution of bins, bin to bin distance.
- RBW: Resolution bandwidth is calculated from the transform resolution and window bandwidth.
- FS: Full scale is the input range, maximum magnitude of sine wave before clipping.
- DNR: Dynamic range is the ratio, in dB, of the largest to the smallest signals that can be detected.
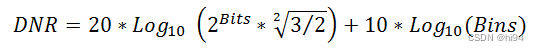
2.3.3 动态指标
- NF: Noise floor is a root mean square (RMS) of all the bins except the peak signal and its harmonics.
- WoSpur: Worst spur level may or may not be a harmonic of the original signal; DC and bins on the descending slope are excluded.
- SFDR: Spurious free dynamic range is the ratio of the RMS value of the peak signal to the RMS value of the worst spurious signal. Expressed in dBc units, with respect to the actual signal amplitude.
- SFDRFS: Spurious free dynamic range, expressed in dBFS units, with respect to full-scale.
- SNR: Signal to noise ratio
- SNRFS: Signal to noise ratio, expressed in dBFS units, with respect to full-scale.
- THD: Total Harmonic Distortion
- SINAD: Signal to noise and distortion, S/(N + D)
- ENOB: Effective number of bits.
3. 其他相关知识
3.1 归一化
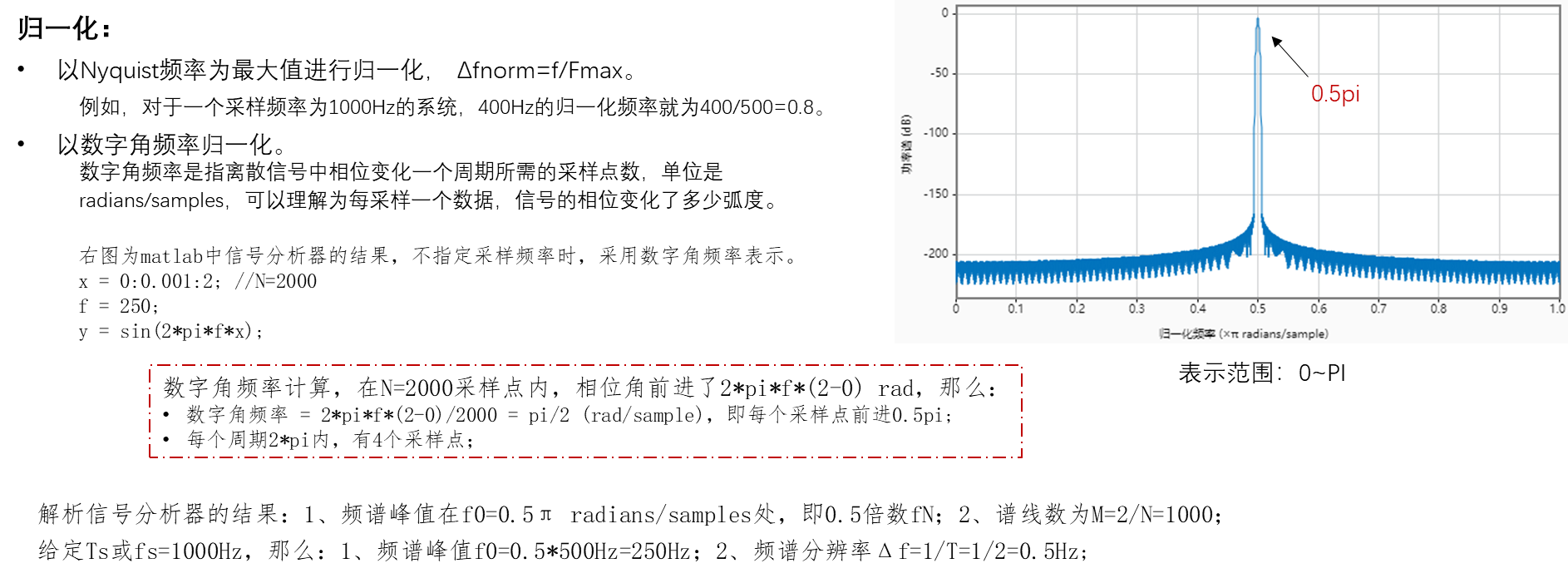
3.2 DFT 示例
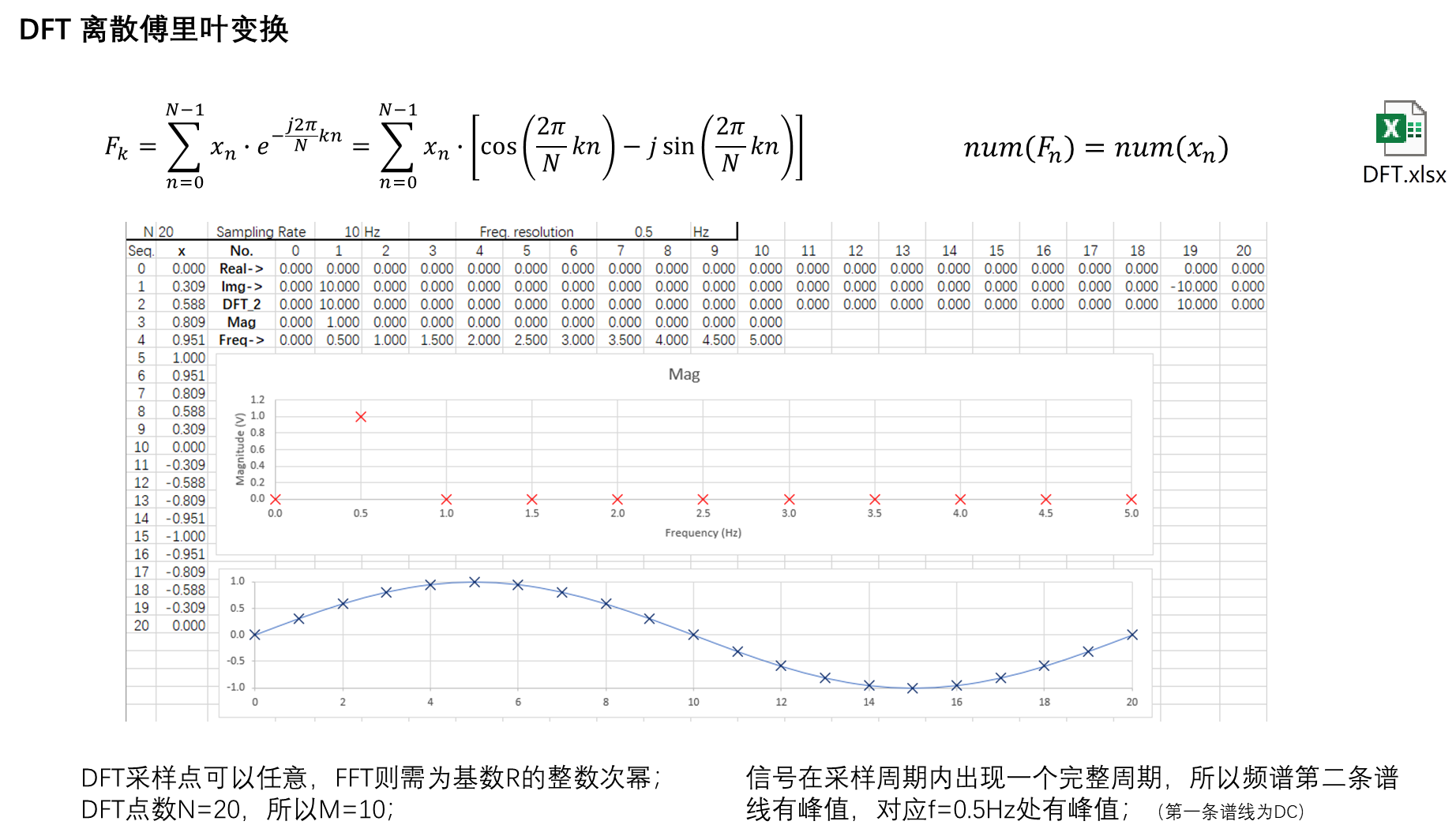
4. 总结
本文介绍了通过AD2记录频谱相关知识的过程,并深入探讨了频谱相关参数、窗函数以及频谱参数。频谱相关参数包括采样时间间隔、采样频率、采样点数等,而窗函数则在傅里叶变换前对信号进行修改,以改善频谱分析结果。频谱参数包括幅值单位解释、常量解释以及动态指标,这些参数对于正确理解频谱图和进行精确的频谱分析很有必要。






)






基本概念)






