工作需要,要基于ubuntu自定义一些编译环境并将自己配置好的ubuntu做成镜像。
硬件准备
为保证能够顺利完成系统iso镜像的制作与系统还原,推荐准备一个较大容量的U盘或者移动固态硬盘,同时确保自己的Ubuntu系统还有比较大的可用空间。
1 Systemback安装
Systemback是一个简单的系统备份和恢复应用程序。Ubuntu 16.04和14.04用户可以通过在终端中运行以下命令从PPA安装Systemback:
# Ubuntu 16.04 or 14.04, ubuntu 18及以后不可用
sudo add-apt-repository ppa:nemh/systemback
sudo apt update
sudo apt install systemback
# ubuntu18不小心添加了上面的ppa库,可以使用下面命令删除
sudo add-apt-repository --remove ppa:nemh/systembackUbuntu 16.04的Systemback二进制文件与Ubuntu 18.04/18.10兼容,因此我们可以使用以下命令进行安装:
# 1)在18.04上添加Ubuntu 16.04 PPA
sudo add-apt-repository "deb http://ppa.launchpad.net/nemh/systemback/ubuntu xenial main"# 2)导入此PPA的GPG签名密钥
sudo apt-key adv --keyserver keyserver.ubuntu.com --recv-keys 382003C2C8B7B4AB813E915B14E4942973C62A1B# 3)更新包列表并安装Systemback:
sudo apt update
sudo apt install systemback# 4)启动 Systemback
sudo systemback2 ISO文件制作
# 启动 Systemback
sudo systemback如果报错:Unsafe X Window authorization!
sudo apt install gksu
gksu systemback
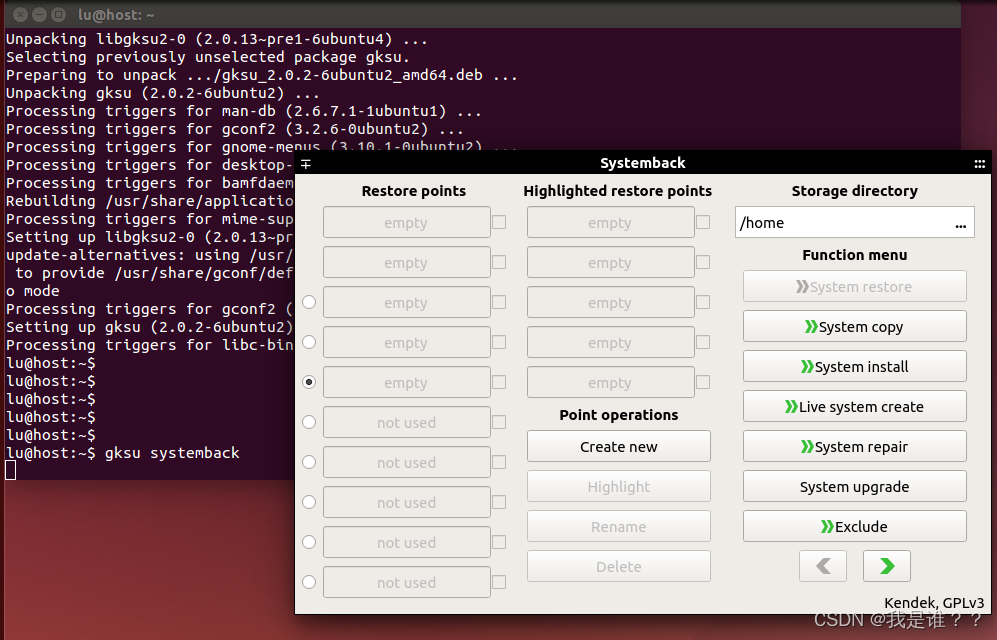
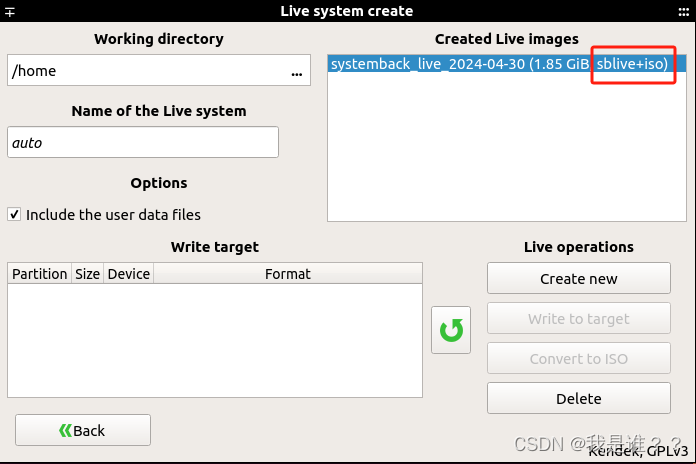
点击“Live system create” —> 修改系统名称,勾选“Include the user data files”—>点击“Create new”。
该操作将会生成一个.sblive文件,如果文件小于4GB,可以借助该软件生成对应的.iso系统镜像文件。
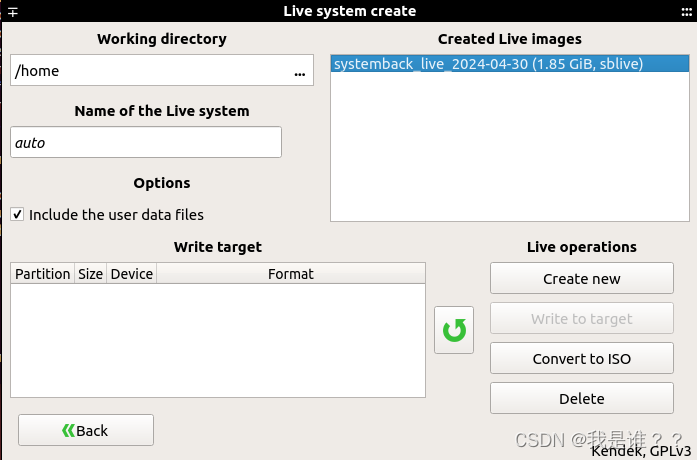
2.1 如果生成的.sblive文件小于4G
可以看到,生成的sblive为1.85G,点击“Convert to ISO”如下。
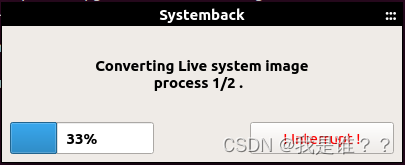
转换完成如下,可以看到会由2个文件,一个是.sblive文件,一个是.iso文件
查看生成的文件
lu@host:~$ ls /home/ -l
total 3883832
drwxr-xr-x 16 lu lu 4096 4月 30 14:43 lu
drwxr-xr-x 2 root root 4096 4月 30 14:40 Systemback
-rw-rw-rw- 1 root root 1989148672 4月 30 15:05 systemback_live_2024-04-30.iso
-rw-rw-rw- 1 root root 1988259840 4月 30 15:01 systemback_live_2024-04-30.sblive
lu@host:~$2.2 如果生成的.sblive文件大于4GB
可以参考下面的步骤生成对应的.iso系统镜像文件。生成.sblive文件袋过程中如果遇到拷贝错误,可以将对应的路径文件“exclude”。如果~/下面有swap分区文件,也需要exclude或者删除掉。删除方法为“sudo swapoff xxx”,然后再“sudo rm -rf xxx”。
步骤1:解压 .sblive 文件:
mkdir sblive
# 【systemback_live.sblive】需要更改为前面设置的名称[也可以直接到home目录下寻找对应的.sblive文件]
tar -xf /home/systemback_live.sblive -C sblive步骤2:重命名syslinux 至 isolinux:
mv sblive/syslinux/syslinux.cfg sblive/syslinux/isolinux.cfg
mv sblive/syslinux sblive/isolinux步骤3:安装 cdtools:
sudo apt install aria2aria2c -s 10 https://nchc.dl.sourceforge.net/project/cdrtools/alpha/cdrtools-3.02a07.tar.gztar -xvf cdrtools-3.02a07.tar.gz
cd cdrtools-3.02
make
sudo make install
步骤4:生成ISO文件:
cd ~/
/opt/schily/bin/mkisofs -iso-level 3 -r -V sblive -cache-inodes -J -l -b isolinux/isolinux.bin -no-emul-boot -boot-load-size 4 -boot-info-table -c isolinux/boot.cat -o sblive.iso sblive这一步完成后,将会生成一个iso文件。



)














:使用 pandas 处理数据并写入 MySQL 数据库)
(64))