【算法一则】【动态规划】求二维数组可组成的最大正方形

题目

在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

示例 1：
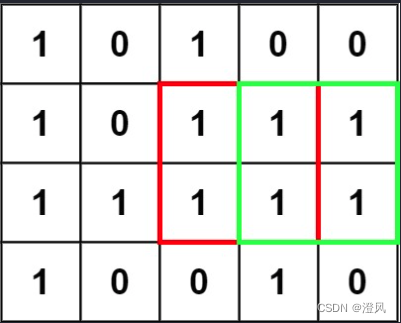
在这里插入图片描述

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：
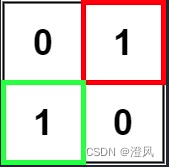
在这里插入图片描述

输入：matrix = [["0","1"],["1","0"]]
输出：1
示例 3：输入：matrix = [["0"]]
输出：0
提示：m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 '0' 或 '1'

题解

这道题目要求找出给定二维字符数组中最大正方形的面积。我们可以使用动态规划的方法来解决这个问题。

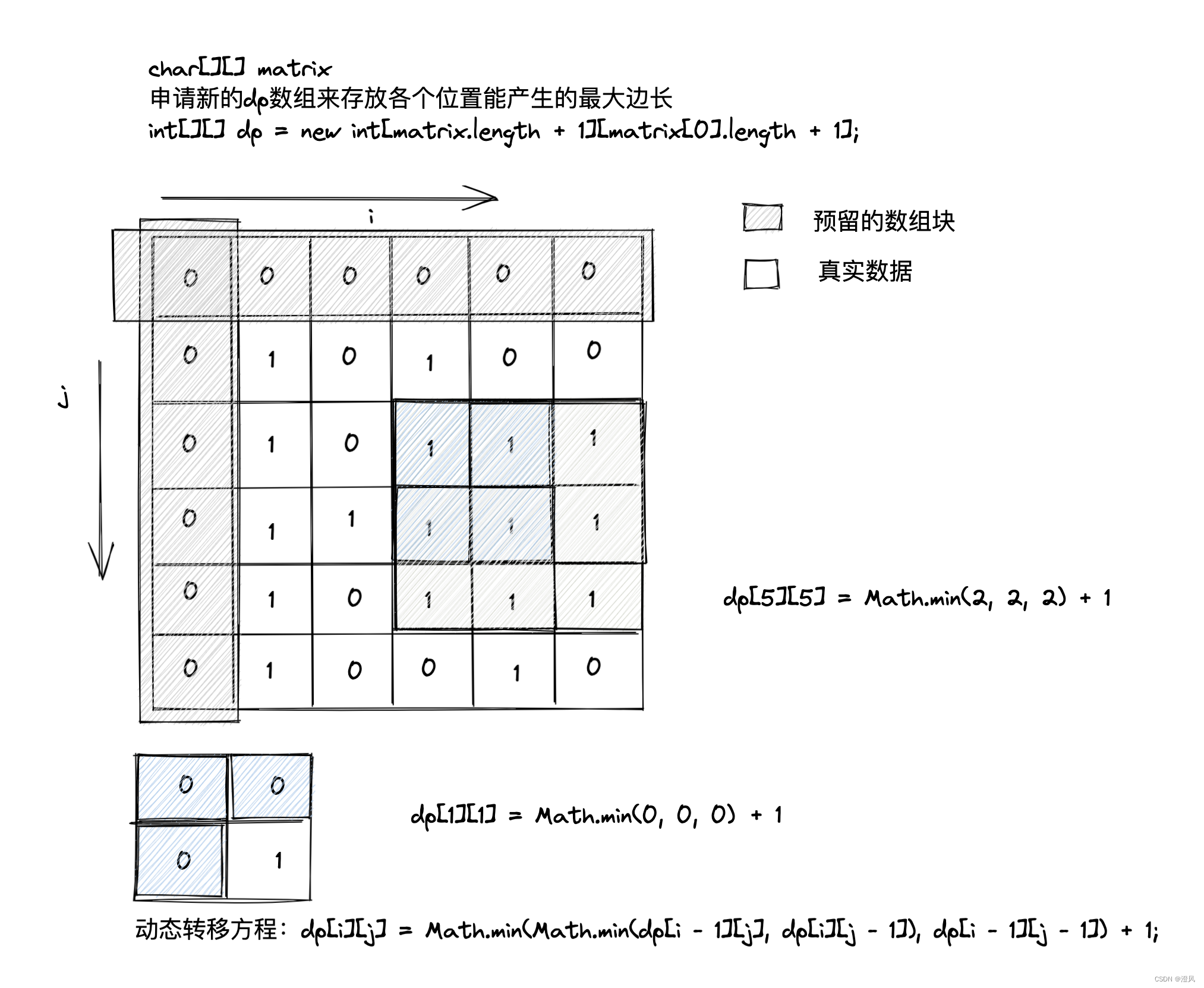
首先，我们定义一个辅助的二维数组dp，其中dp[i][j]表示以matrix[i-1][j-1]为右下角的最大正方形的边长。

然后，我们遍历二维数组matrix，从左上角开始，对于每个位置(i, j)，如果该位置的字符为’1’，则计算以该位置为右下角的最大正方形的边长。

计算以当前位置为右下角的最大正方形的边长时，我们可以使用动态规划的思想。我们比较当前位置的左边、上边和左上角三个位置的最小边长，再加上1，即可得到以当前位置为右下角的最大正方形的边长。

在计算过程中，我们还需要维护一个变量maxSide，用于记录当前找到的最大正方形的边长。

最后，函数返回最大正方形的面积，即maxSide的平方。

算法的时间复杂度是O(m×n)，其中m是二维数组的行数，n是二维数组的列数。空间复杂度是O(m×n)
O(m×n)，因为我们使用了一个辅助的二维数组dp。

在这里插入图片描述

public class MaximalSquare {public int maximalSquare(char[][] matrix) {int maxSide = 0; // 记录最大正方形的边长int[][] dp = new int[matrix.length + 1][matrix[0].length + 1]; // 创建一个二维数组用于动态规划for (int i = 1; i <= matrix.length; i++) {for (int j = 1; j <= matrix[0].length; j++) {if (matrix[i - 1][j - 1] == '1') { // 如果当前位置是 '1'// 计算以当前位置为右下角的最大正方形的边长，并更新maxSidedp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;maxSide = Math.max(maxSide, dp[i][j]);}}}return maxSide * maxSide; // 返回最大正方形的面积}@Testpublic void testMain() {// 测试用例1char[][] matrix = {{'1','0','1','0','0'},{'1','0','1','1','1'},{'1','1','1','1','1'},{'1','0','0','1','0'}};System.out.println(maximalSquare(matrix));// 测试用例2char[][] matrix1 = {{'0','1'},{'1','0'}};System.out.println(maximalSquare(matrix1));// 测试用例3char[][] matrix2 = {{'0'}};System.out.println(maximalSquare(matrix2));}
}

该代码实现了一个函数maximalSquare，用于计算给定二维字符数组matrix中最大正方形的面积。算法使用动态规划的思想，通过填充一个辅助的二维数组dp来记录以每个位置为右下角的最大正方形的边长。

maximalSquare函数首先初始化一个变量maxSide为0，用于记录最大正方形的边长。然后创建一个大小为(matrix.length + 1) × (matrix[0].length + 1)的二维数组dp，其中dp[i][j]表示以matrix[i-1][j-1]为右下角的最大正方形的边长。

接下来，使用两个嵌套的循环遍历二维数组matrix，从左上角开始，对于每个位置(i, j)，如果该位置的字符为'1'，则计算以该位置为右下角的最大正方形的边长，并更新maxSide。

计算以当前位置为右下角的最大正方形的边长时，使用动态规划的思想，通过比较左边、上边和左上角三个位置的最小边长，再加上1，得到以当前位置为右下角的最大正方形的边长。

最后，函数返回最大正方形的面积，即maxSide的平方。

testMain函数是一个测试函数，用于测试maximalSquare函数的功能。它包含了三个测试用例，分别对应不同的输入情况，输出结果为最大正方形的面积。