计算斐波那契数列第n项的快速算法(矩阵的n次幂)
The n-th term of Fibonacci Numbers:
斐波那契数列的是一个古老而又经典的数学数列,距今已经有800多年了。关于斐波那契数列的计算方法不难,只是当我们希望快速求出其数列中的第100,乃至第1000项时,有没有又准又快的方法,一直是一个值得探讨和研究的问题。笔者(松下J27)在这篇文章中,就介绍了一种基于线性代数的快速算法,即,基于矩阵的n次幂找到斐波那契数列的第n项。这是我在MIT线性代数的公开课中看到的,并以此文记录下来。

(意大利数学家斐波那契,图片来源于参考文献【1】)
已知斐波那契数列的数学表示方式如下:
他始于数列的前两个初始值0,1,后面所有的项都是前两项的和,依此类推得到:
,
,
,
,
。。。
基于上面的计算规律,假设我用来表示该数列的第i个数的话,那斐波那契数列用代数的方式可写成两个初值和一个递归公式的组合,即:
现在把上面的公式用矩阵和向量的方式来表示,以便于用线性代数来分析:
1,先把初值用向量u0来表示
2,用向量表示数列中的第n项。
3,如此一来根据递归公式就能写出第i+1项
4,用矩阵来表示从第i项到第i+1项
的过程
其中,参与计算的矩阵A为:
现在,我们知道了初始向量,也知道如果计算
,我们就能通过线性代数中矩阵与向量的计算来计算斐波那契数列中的任意一项:

可以看到,如果你要计算第100项,不出意外,只要把上述步骤继续下去一定能够找到。另外,如果把上述计算中的三次计算合成一部,就是三个矩阵A连续相乘后,再乘以u0。

这就是说,斐波那契数列中第n项的计算公式应该是:
, (式1)
这里要注意的是,根据这种方法算出来的是一个向量,而我们需要的结果,即,第n项是该向量中的第一个元素。
引入矩阵的对角化:
熟悉线性代数的朋友看到A的n次幂时,马上就会想到是否可以通过特征向量矩阵X和特征值矩阵对A进行对角化。
线性代数 --- 矩阵的对角化以及矩阵的n次幂-CSDN博客文章浏览阅读1k次,点赞15次,收藏9次。本文从矩阵A的对角化开始,一直聊到了对角化的应用,并以一个A的n次幂为例子结尾。https://blog.csdn.net/daduzimama/article/details/138088128
因为,如果方阵A可以被对角化为:
那么上面推导出来的斐波那契数列的第n项的计算公式就能简化为:
, (式2)
现在我们试着用(式2)去计算斐波那契数列的第100项:
第一步,计算矩阵A的特征向量与特征值:

通过计算得出了两个不同的特征值,说明矩阵A可以对角化。
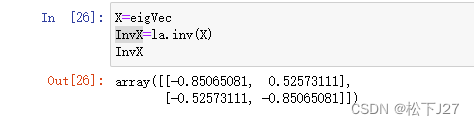
第二步,构建特征向量矩阵X,特征值矩阵和特征向量矩阵的逆:
第三步,计算特征值矩阵的100次幂:

第四步,基于(式2)去计算第100项的值:
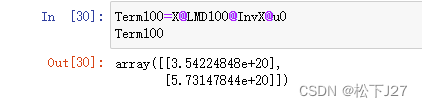
其中,第100项的值为:
进一步简化:
如果我能把u0表示成所有特征向量的线性组合的话,就能更进一步简化计算:
, (式3)
其中,权重系数向量c等于:
, (式4)
如此一来,斐波那契的第n项的计算公式(式1)就变成了:
, (式5)
又因为这里的x都是特征向量,根据特征向量的性质,我们有Key Equation:
对于上式中的第一项有:
因为是一个系数,所以我们把他提到前面去:
这样一来又出现了一个,继续:
如此反复,一直到第n个乘法:
依此类推,(式5)可改写成:
, (式6)
(式6) 也可以写成:
, (式7)
这一点也可以通过把 (式3)代入(式2)得到(式7):
这里面最重要的是(式6),因为他把计算分离开了,分成了一个个常数与向量的乘积之和。
现在针对这一简化算法做一个小结,并以求斐波那契的第100项为例:
第一步,优先使用(式4)算出权重向量c
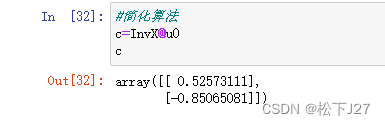
第二步,分别计算和
,其中c和
都是常数。

第三步,求和。把第二步的结果加在一起,求出最终的结果。在本例中,因为中的元素几乎为0,所以他们二者的和几乎约等于
。

最终,得到了同样正确的结果:
(全文完)
--- 作者,松下J27
参考文献(鸣谢):
1,https://zh.wikipedia.org/wiki/%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91
2, Lec22_对角化和矩阵乘幂_哔哩哔哩_bilibili

(配图与本文无关)
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27




)











)


)