本文解决几个问题:
回溯算法是什么?解决回溯算法相关的问题有什么技巧?回溯算法代码是否有规律可循?
一、介绍
1.回溯算法是什么?
回溯算法就是个多叉树的遍历问题,关键在于在前序和后序时间点做一些操作,本质是一种暴力枚举算法,它和DFS非常相似,区别在于,回溯算法关注点在于树的树枝,DFS关注点在于树的节点。
2.回溯算法的技巧
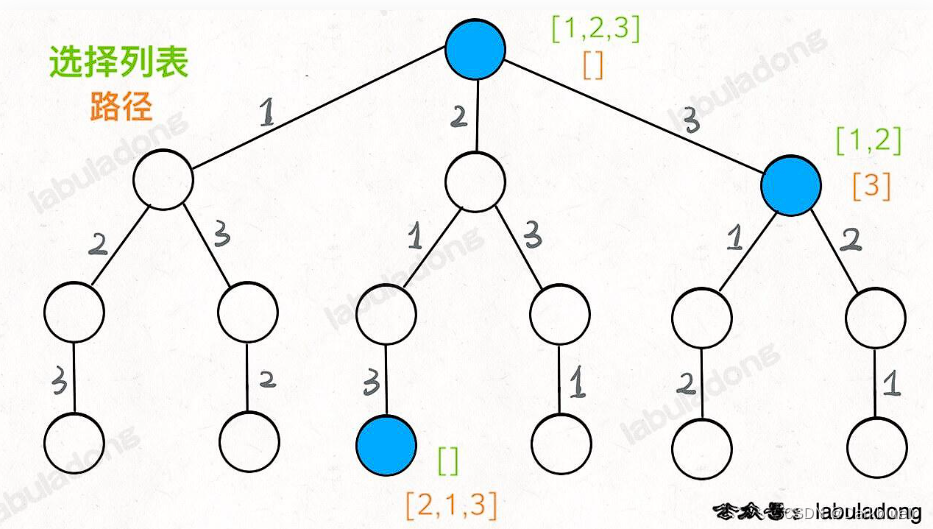
站在一棵决策树的节点,需要考虑三个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
3. 回溯算法的框架(规律)
result = []
def backtrack(路径,选择列表){if(满足结束条件){result.add(路径)return;}for(选择 : 选择列表){//做选择将该选择从选择列表移除路径.add(选择)backtrack(路径, 选择列表)//撤销选择路径.remove(选择)将该选择再加入选择列表}}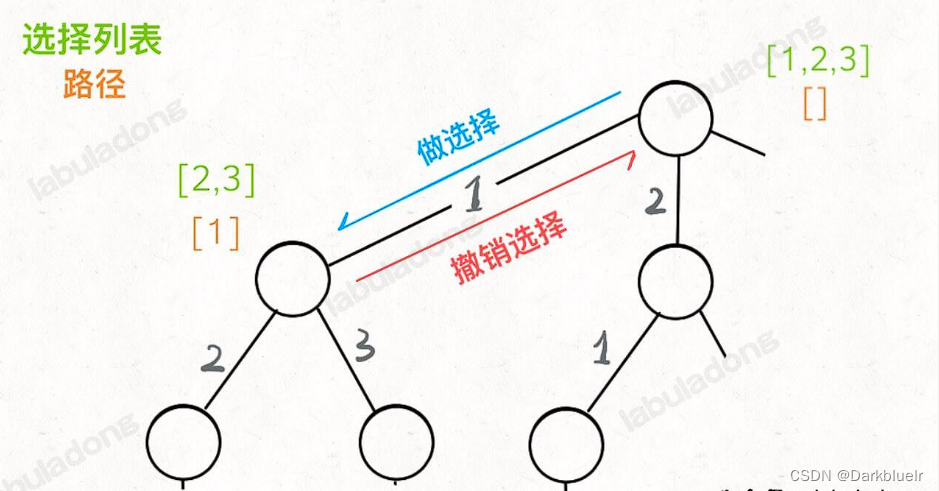
其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」,其实就是在维护每个节点的路径和选择列表信息,
抽象地说,解决一个回溯问题,实际上就是遍历一棵决策树的过程,树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍,把叶子节点上的答案都收集起来,就能得到所有的合法答案。
我们定义的 backtrack 函数在这棵树上游走,同时要正确维护每个节点的属性,每当走到树的底层叶子节点,其「路径」就是一个答案。
4. 回溯算法和DFS的关系
回溯法 采用试错的思想,它尝试分步的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现,在反复重复上述的步骤后可能出现两种情况:
i)找到一个可能存在的正确的答案;
ii)在尝试了所有可能的分步方法后宣告该问题没有答案。
深度优先搜索 是一种用于遍历或搜索树或图的算法。这个算法会 尽可能深 的搜索树的分支。当结点 v 的所在边都己被探寻过,搜索将 回溯 到发现结点 v 的那条边的起始结点。这一过程一直进行到已发现从源结点可达的所有结点为止。如果还存在未被发现的结点,则选择其中一个作为源结点并重复以上过程,整个进程反复进行直到所有结点都被访问为止。
5. 回溯算法的拓展
由于回溯算法的时间复杂度很高,因此在遍历的时候,如果能够提前知道这一条分支不能搜索到满意的结果,就可以提前结束,这一步操作称为 剪枝。剪枝是一种技巧,通常需要根据不同问题场景采用不同的剪枝策略,需要在做题的过程中不断总结。
二、排列、组合、子集相关问题
无论是排列、组合还是子集问题,简单说无非就是让你从序列 nums 中以给定规则取若干元素,主要有以下几种变体:
形式一、元素无重不可复选
形式二、元素可重不可复选
形式三、元素无重可复选
但无论形式怎么变化,其本质就是穷举所有解,而这些解呈现树形结构,所以合理使用回溯算法框架,稍改代码框架即可把这些问题一网打尽。
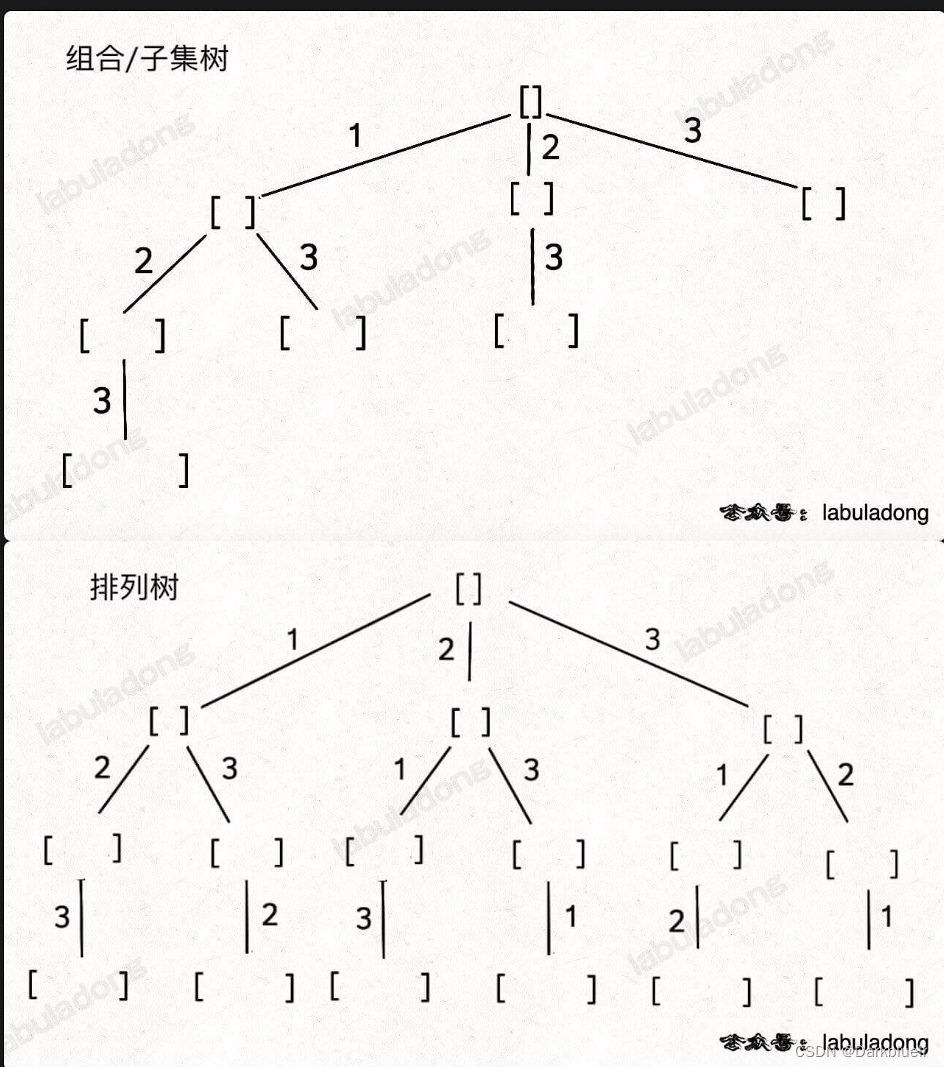
为什么只要记住这两种树形结构就能解决所有相关问题呢?
首先,组合问题和子集问题其实是等价的,这个后面会讲;至于之前说的三种变化形式,无非是在这两棵树上剪掉或者增加一些树枝罢了。
无重不可复选
核心:通过保证元素之间的相对顺序不变来防止出现重复的子集。
具体方法:使用 start 参数控制树枝的生长避免产生重复的子集,用 track 记录根节点到每个节点的路径的值,同时在前序位置把每个节点的路径值收集起来,完成回溯树的遍历就收集了所有子集。
例题1:子集
代码:
class Solution {
public:vector<vector<int>> ans;vector<int> track;void traceback(vector<int>& nums, int start){// 每个节点的值都是一个子集ans.emplace_back(track);for(int i = start; i < nums.size(); i++){track.emplace_back(nums[i]);traceback(nums, i+1);track.pop_back();}}vector<vector<int>> subsets(vector<int>& nums) {traceback(nums, 0);return ans;}
};例题2:组合
分析:
代码:
class Solution {
public:vector<vector<int>> ans;vector<int> track;void backtrack(int n, int k, int start){if(track.size() == k){ans.emplace_back(track);}for(int i = start; i<= n; i++){track.emplace_back(i);backtrack(n, k, i+1);track.pop_back();}}vector<vector<int>> combine(int n, int k) {backtrack(n, k, 1);return ans;}
};例题3:全排列
分析:
选择列表就是遍历整个数组,如果没有用过某个数字,就选择它,然后把used数组对应的值设为true,然后进入节点(递归调用backtrack()),出来后撤销选择,方式是对路径弹出元素,然后更新used数组。
代码:
class Solution {
public:vector<vector<int>> ans;vector<vector<int>> permute(vector<int>& nums) {vector<int> track;vector<bool> used(nums.size(), false);backtrack(nums, track, used);return ans;}void backtrack(vector<int>&nums, vector<int>&track, vector<bool>& used){if(track.size() == nums.size()){ans.push_back(track);return;}for(int i =0; i < nums.size(); i++){if(used[i] == true){continue;}track.push_back(nums[i]);used[i] = true;backtrack(nums, track, used);track.pop_back();used[i] = false;}}
};但如果题目不让你算全排列,而是让你算元素个数为 k 的排列,怎么算?
也很简单,改下 backtrack 函数的 base case,仅收集第 k 层的节点值即可
可重不可复选
例题4:子集 II
分析:
元素可重的通用解决方法:排序 + used数组,连续相同的元素只能按顺序取,不能前面的没取取后面的。
代码:
class Solution {
public:vector<vector<int>> ans;vector<int> track;void backtrack(vector<int>& nums, int start, vector<bool> used){ans.emplace_back(track);for(int i = start; i<nums.size(); i++){// 剪枝逻辑,值相同的相邻树枝,只遍历第一条if(i>0 && nums[i] == nums[i-1] && used[i-1] == false){continue;}track.emplace_back(nums[i]);used[i] = true;backtrack(nums, i+1, used);used[i] = false;track.pop_back();}}vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(), nums.end());vector<bool> used(nums.size(), false);backtrack(nums, 0, used);return ans;}
};例题5:组合总和 II
代码:
class Solution {
public:vector<int> track;vector<vector<int>> ans;void traceback(vector<int>& candidates, int target, vector<bool>& used, int start){int sum = accumulate(track.begin(), track.end(), 0);if(sum == target){ans.emplace_back(track);return;}if(sum > target){return;}for(int i = start ; i< candidates.size(); i++){if(used[i] || ( i>0 && candidates[i-1] == candidates[i] && used[i-1] == false)){continue;}used[i] = true;track.emplace_back(candidates[i]);traceback(candidates, target, used, i+1);track.pop_back();used[i] = false;}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(), candidates.end());vector<bool> used(candidates.size(), false);traceback(candidates, target, used, 0);return ans;}
};例题6:全排列 II
分析:
所有相同的数字,他的排列组合只有一个,记住这一点,然后用nums[i-1] == nums[i] && used[i-1] == false这个条件去限制,就可以做到相同数字只有一个排列进入答案。
代码:
class Solution {
public:vector<vector<int>> ans;void backtrack(vector<int>& nums, vector<int>& track, vector<bool>& used){if(track.size() == nums.size()){ans.push_back(track);return;}for(int i = 0; i< nums.size(); i++){if(used[i]==true || (i > 0 && nums[i-1] == nums[i] && used[i-1] == false)){continue;}used[i] = true;track.push_back(nums[i]);backtrack(nums, track, used);track.pop_back();used[i] = false;}}vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(), nums.end());vector<int> track;vector<bool> used(nums.size(), false);backtrack(nums, track, used);return ans;}
};元素无重可复选
例题7:组合总和
分析:
想解决这种类型的问题,也得回到回溯树上,我们不妨先思考思考,标准的子集/组合问题是如何保证不重复使用元素的?
答案在于 backtrack 递归时输入的参数 start,这个 i 从 start 开始,那么下一层回溯树就是从 start + 1 开始,从而保证 nums[start] 这个元素不会被重复使用,那么反过来,如果我想让每个元素被重复使用,我只要把 i + 1 改成 i 即可:
代码:
class Solution {
public:vector<vector<int>> ans;vector<int> track;int sum;void backtrack(vector<int>& nums, int target, int start){sum = accumulate(track.begin(), track.end(), 0);if(sum > target){return;}if(sum == target){ans.emplace_back(track);return;}for(int i = start; i<nums.size(); i++){track.emplace_back(nums[i]);backtrack(nums, target, i);track.pop_back();}}vector<vector<int>> combinationSum(vector<int>& nums, int target) {backtrack(nums, target, 0);return ans;}
};其他
例题8:排列序列
代码:
思路1:回溯 + 剪枝
class Solution {
public:vector<vector<char>> ans;vector<char> track;int cnt = 0;void backtrack(int n, vector<bool> used){if(track.size() == n){ans.emplace_back(track);cnt++;return;}for(int i = 0; i< n; i++){if(used[i]){continue;}track.emplace_back(i+1+'0');used[i] = true;backtrack(n, used);used[i] = false;track.pop_back();}}string getPermutation(int n, int k) {vector<bool> used(n, false);//如果数字过大,直接定位第一位if( k > 120){int factorial = 1;int first;for(int i = 1; i < n; i++){factorial *= i;}first = k/factorial;k %= factorial;track.emplace_back(first + 1 + '0');used[first] = true;}//业务逻辑backtrack(n, used);string ret(ans[k-1].begin(), ans[k-1].end());return ret;}
};思路2:直接定位
class Solution {
public:string getPermutation(int n, int k) {vector<char> ans, array;int tmp, ncp = n, f = 1;array.emplace_back('1');for(int i = 1; i < ncp; i++){f*= i;array.emplace_back(i+1+'0');}f*= ncp;k--;while(n != 0){f /= n--;tmp = k/f;k %= f;ans.emplace_back(array[tmp%ncp]);array.erase(array.begin() + tmp);}string ret(ans.begin(), ans.end());return ret;}
};例题9:复原 IP 地址
代码:
class Solution {
public:vector<string> ans;vector<int> segment;void backtrack(string s,int pos, int segcnt){int segnum = 0;if(pos == s.size() && segcnt == 4){string track;for(int i = 0; i< 4; i++){track += to_string(segment[i]);if(i != 3) track += '.';}ans.emplace_back(track);//到达末尾return回去return;}else if((segcnt == 4 && pos != s.size()) || (pos == s.size() && segcnt != 4)){return;}if(s[pos] == '0'){segment[segcnt] = 0;backtrack(s, pos + 1, segcnt + 1);//撤销选择的方法是returnreturn;}for(int i = pos; i<s.size(); i++){segnum = segnum*10 + (s[i] - '0');if(segnum > 0 && segnum <= 0xFF){segment[segcnt] = segnum;backtrack(s, i+1, segcnt + 1);}else{return;}}}vector<string> restoreIpAddresses(string s) {segment.resize(4);backtrack(s, 0, 0);return ans;}
};三、Flood Fill(DFS)
例题10:单词搜索
分析:
本题说是回溯,其实很像DFS的方法,参考:
DFS 算法解决岛屿题目
代码:
class Solution {
public:int m, n;bool backtrack(vector<vector<char>>& board, string word, int pos, int i, int j){if(i >= m || j >= n || i<0 || j<0 || board[i][j] != word[pos]){return false;}if(pos == word.size()-1){return true;}bool res;board[i][j] = 0;res = backtrack(board, word, pos+1, i+1, j) || backtrack(board, word, pos+1, i-1, j)||backtrack(board, word, pos+1, i, j+1) || backtrack(board, word, pos+1, i, j-1);board[i][j] = word[pos];return res;}bool exist(vector<vector<char>>& board, string word) {m = board.size();n = board[0].size();for(int i = 0; i< m; i++){for(int j = 0; j<n; j++){if(backtrack(board, word, 0, i, j))return true;}}return false;}
};例题11:被围绕的区域
DFS 算法解决岛屿题目 中有详解
例题12:岛屿数量
DFS 算法解决岛屿题目 中有详解
例题13:图像渲染
分析:
dfs模板:越界返回
访问返回
非目标返回
dfs递归
代码:
class Solution {
public:int m, n;int samecolor;void dfs(vector<vector<int>>& image, int i, int j, int color){if(i>=m || j>= n|| i<0 || j<0){return;}if(image[i][j] == color){return;}if(image[i][j] != samecolor){return;}image[i][j] = color;dfs(image, i+1, j, color);dfs(image, i, j+1, color);dfs(image, i, j-1, color);dfs(image, i-1, j, color);}vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {m = image.size(); n = image[0].size();samecolor = image[sr][sc];dfs(image, sr, sc, color);return image;}
};
三、字符串中的回溯问题
例题14:电话号码的字母组合
代码:
class Solution {
public:vector<string> ans;string track;vector<string>array;void backtrack(string digits, int pos){if(track.size() == digits.size()){ans.emplace_back(track);return;}//根据数字算出其对应的选择有哪些for(char c : array[digits[pos]-'0']){track += c;backtrack(digits, pos+1);track.erase(track.end()-1);}}vector<string> letterCombinations(string digits) {if(digits.size() == 0){return ans;}array.resize(10);for(int i = 0; i<18; i++){array[i/3+2] += i+'a';}array[7] += 's'; array[8] = "tuv"; array[9] = "wxyz";backtrack(digits, 0);return ans;}
};改良:这里用hashmap存储选择数组比较好
class Solution {
public:vector<string> ans;string track;unordered_map<char, string> array;void backtrack(string digits, int pos){if(track.size() == digits.size()){ans.emplace_back(track);return;}for(char c : array[digits[pos]]){track += c;backtrack(digits, pos+1);track.erase(track.end()-1);}}vector<string> letterCombinations(string digits) {if(digits.size() == 0){return ans;}array = {{'2', "abc"},{'3', "def"},{'4', "ghi"},{'5', "jkl"},{'6', "mno"},{'7', "pqrs"},{'8', "tuv"},{'9', "wxyz"}};backtrack(digits, 0);return ans;}
};
例题15:字母大小写全排列
代码:
class Solution {
public:vector<string> ans;string track;string choice(char c){string ret;ret += c;if(c >= 'a' && c <= 'z'){ret += toupper(c);}if(c >= 'A' && c <= 'Z'){ret += tolower(c);}return ret;}void backtrack(string s, int pos){if(track.size() == s.size()){ans.emplace_back(track);return;}//做选择for(char c : choice(s[pos])){track += c;backtrack(s, pos+1);track.erase(track.end()-1);}}vector<string> letterCasePermutation(string s) {backtrack(s, 0);return ans;}
};例题16:括号生成
分析:
代码:
三、游戏问题
例题17:N 皇后
分析:
代码:
例题18:解数独
分析:
代码:
例题19:祖玛游戏
分析:
代码:
例题20:扫雷游戏
分析:
代码:
四、总结
i)全排列解决方法:
用used数组来选取没有选过的元素
ii)元素可重的通用解决方法:
排序 + used 数组,连续相同的元素只能按顺序取,不能前面的没取取后面的。
iii)组合/子集(非排列)解决方法:
backtrack传start进去,控制取元素的顺序,避免重复访问。
可重复选:递归的时候传 i
不可重复选:递归的时候传 i + 1
比如,[1, 2, 3],固定一的时候[1,3]取走了,下一次固定3,如果不控制顺序,还会取到[3,1],这样按组合的逻辑来说就是重复的。
iii)只要从树的角度思考,这些问题看似复杂多变,实则改改 base case 就能解决
iv)vector<char>转化为string:直接string str(v.begin(), v.end());
v)string删去最后一个元素: string.erase(string.end()-1);



)








—— 随机森林)


—context: component-scan标签如何扫描、加载Bean)

)
)
