系列文章:
操作系统详解(1)——操作系统的作用
操作系统详解(2)——异常处理(Exception)
操作系统详解(3)——进程、并发和并行
操作系统详解(4)——进程控制(fork, waitpid, sleep, execve)
操作系统详解(5)——信号(Signal)
文章目录
- 一些概念
- CPE
- 初步优化
- 消除不必要的函数调用
- 消除不必要的内存引用
- 基于处理器机制的深度优化
- 现代处理器
- 超标量(Superscalar)
- 乱序执行
- 处理器结构
- 寄存器重命名
- 多核处理器
- 数据流图
- 分析
- 促进并发(parallelism)
- n*1 循环展开
- n*n循环展开
- 吞吐量界限(Throughout)
- 不同的运算结合
- 优化的限制因素
- 寄存器溢出
- 分支预测
如何优化一个程序的运行速度?可以从以下几个方面着手:
- 算法
- 数据结构
- 执行的步骤
- 循环
本文将主要从计算机系统底层方面,探讨如何降低运行时间。
一些概念
CPE
即Cycles Per Element, 运行每一个操作需要的时钟周期
T = CPE*n + Overhead
n: 操作数量
overhead: 其它操作时延
初步优化
以下是一个粗糙的c程序代码:
void combine1(vec_ptr v, data_t *dest)
{long i;*dest = IDENT;for (i = 0; i < vec_length(v); i++) {data_t val;get_vec_element(v, i, &val);*dest = *dest OP val;}
}
/*
v: 一个向量
dest: 存储执行结果
OP: 运算符, 可以是+, *等
vec_length: 返回向量长度
get_vec_element: 范围下标为i的元素, 存放在val中
IDENT: 单位元, 加法就是0, 乘法就是1
*/
CPE如下:(Element为执行一次循环)

可见gcc自带的优化也能对性能起到很大影响.本例中是O1优化.
消除不必要的函数调用
void combine2(vec_ptr v, data_t *dest)
{long i;long length = vec_length(v);*dest = IDENT;for (i = 0; i < length; i++) {data_t val;get_vec_element(v, i, &val);*dest = *dest OP val;}
}
由于v的长度是定长的, 不会被循环改变, 所以可以在循环前面先得到, 这样就不用每次循环都调用一次了.

在本例中优化幅度很小.但是由于length()的时间复杂度是O(n), 当v的长度很大的时候, 循环执行n次, 时间复杂度为O(n^2), 增长速度远远大于O(n)
消除不必要的内存引用
假设v结构体中存储数据的部分是一个数组, 我们用get_vec_start函数能够获取v的指向数组开头的指针, 那么可以得到一下代码:
void combine3(vec_ptr v, data_t *dest)
{long i;long length = vec_length(v);data_t *data = get_vec_start(v);*dest = IDENT;for ( i = 0 ; i < length ; i++ ) {*dest = *dest OP data[i] ;
}

虽然消除了函数调用, 由于compiler已经帮我们做了很多优化, 所以转成汇编代码后效率并不会差距很大.
我们看一下汇编代码:
combine3: data_t = double, OP = *data+length in %rax, data+i in %rdx, dest in %rbx1 .L17: loop:
2 vmovsd (%rbx), %xmm0 Read product from dest
3 vmulsd (%rdx), %xmm0, %xmm0 Multiply product by data[i]
4 vmovsd %xmm0, (%rbx) Store product at dest
5 addq $8, %rdx Increment data+i
6 cmpq %rax, %rdx Compare to data+length
7 jne .L17 If !=, goto loop
我们发现, 每一次都要先从内存中取出(%rbx), 即*dest中存储的值, 运算以后还要写回(%rbx), 如果将代码改为下面:
void combine4(vec_ptr v, data_t *dest)
{long i;long length = vec_length(v);data_t *data = get_vec_start(v);data_t acc = IDENT;for (i = 0; i < length; i++)acc = acc OP data[i];*dest = acc;
}combine4: data_t = double, OP = *data+length in %rax, data+i in %rdx, limit in %rbp, acc in %xmm01 .L25: loop:
2 vmulsd (%rdx), %xmm0, %xmm0 Multiply acc by data[i]
3 addq $8, %rdx Increment data+i
4 cmpq %rax, %rdx Compare to data+length
5 jne .L25 If !=, goto loop
- 运算结果存储在寄存器中
- 避免循环一次执行一组额外的读写
- 最后再写入内存即可
这是由于读写涉及内存访问, 而这比访问寄存器慢数万倍.

这难道就是优化的极限了吗?
基于处理器机制的深度优化
现代处理器
超标量(Superscalar)
能够实现指令(instruction)层面的并行执行, 一个clock cycle执行多条指令
乱序执行
(只要不影响程序执行结果), 指令的执行顺序可以与汇编语句的顺序不同.
处理器结构
这部分的实际设计思想比较复杂, 本文只是简要提及几个重要概念.
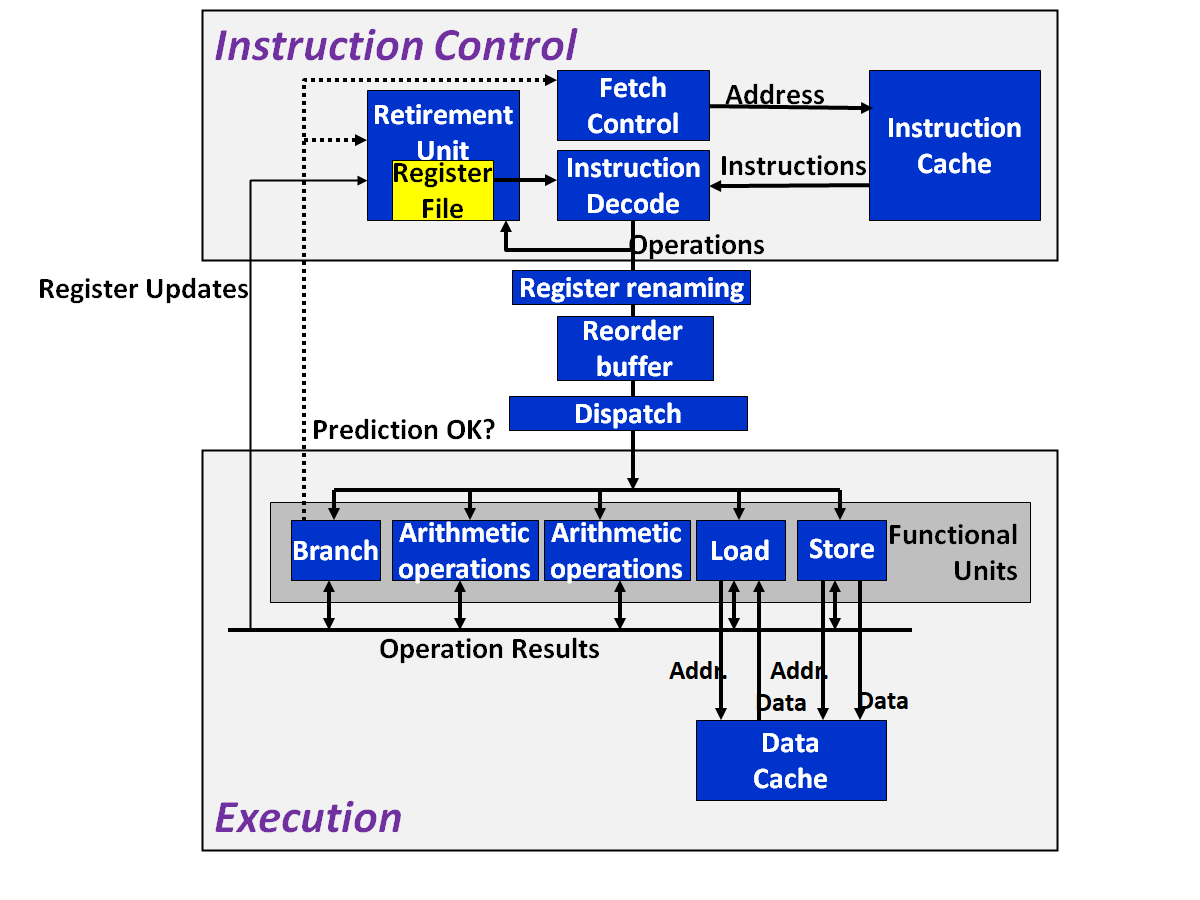
微操作:Instruction Decode Unit 读取程序的指令,并将它们分解为更细的基础操作。
比如说,一条汇编语句addq %rax, 8(%rdx)可以被分解为:
load 8(%rdx) -> t1
addq %rax, t1 -> t2
store t2, 8(%rdx)
其中load, addq(运算), store就是基础的操作。
寄存器重命名
addq $8, %rdx 被翻译为
addq $8, %rdx.0 -> %rdx.1
寄存器名后面的 .t 表示一个标签,用来标识操作的执行顺序。
多核处理器
在上图中, Execution Unit 从 Instruction Control Unit 得到需要执行的操作,在么一个时钟周期能执行一组操作。
现代的处理器都有多个处理单元。以Intel i7处理器为例,其处理单元如下:

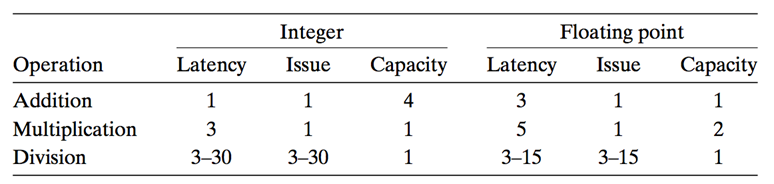
下面解释一下几个名词的意思:
Latency: 就是执行一条操作需要的时间。比如上表中的第一行第一列,Integer Addition的Latency是1,说明执行1条整数加法需要1个时钟周期。而执行一次浮点数乘法需要5个时钟周期。
Issue: 中文又译作“发射”时间。比方说,一个整数乘法需要3个时钟周期,但如果用pipeline执行,每一个clock都能“发射”一条微指令,这样每一个clock都能执行一条指令.
Capacity: 容量,即处理器有几个该运算的处理单元。从上图可知,有4个Integer arithmetic Unit (整数运算单元),故Capacity为4.
数据流图
Data-Flow Graphs, 用于可视化程序的数据依赖.
以combie4为例 (data_t ) = float, OP = *
void combine4(vec_ptr v, data_t *dest)
{long i;long length = vec_length(v);data_t *data = get_vec_start(v);data_t x = IDENT;for (i = 0; i < length; i++)x = x OP data[i];*dest = x;
}
汇编:
.L25: # Loop:
vmulsd (%rdx),%xmm0,%xmm0 # x *= data[i]
addq $8, %rdx # Increment data+i
cmpq %rax,%rdx # Comp to data+len
jne .L25 # if !=, goto Loop
微指令:
load (%rdx.0) -> t.1
mulq t.1, %xmm0.0 -> %xmm0.1
addq $8, %rdx.0 -> %rdx.1
cmpq %rax, %rdx.1 -> cc.1
jne-taken cc.1
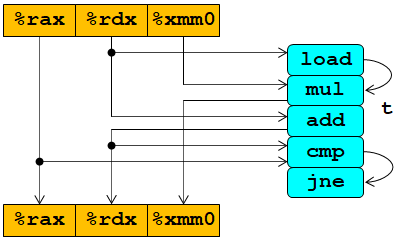
更清晰的图:
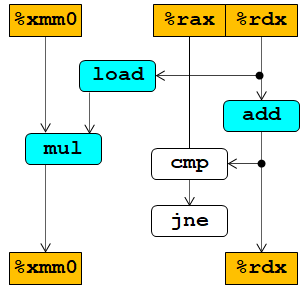
此图显示出,只有当load执行以后,mul才能执行,因为mul对load有数据依赖.
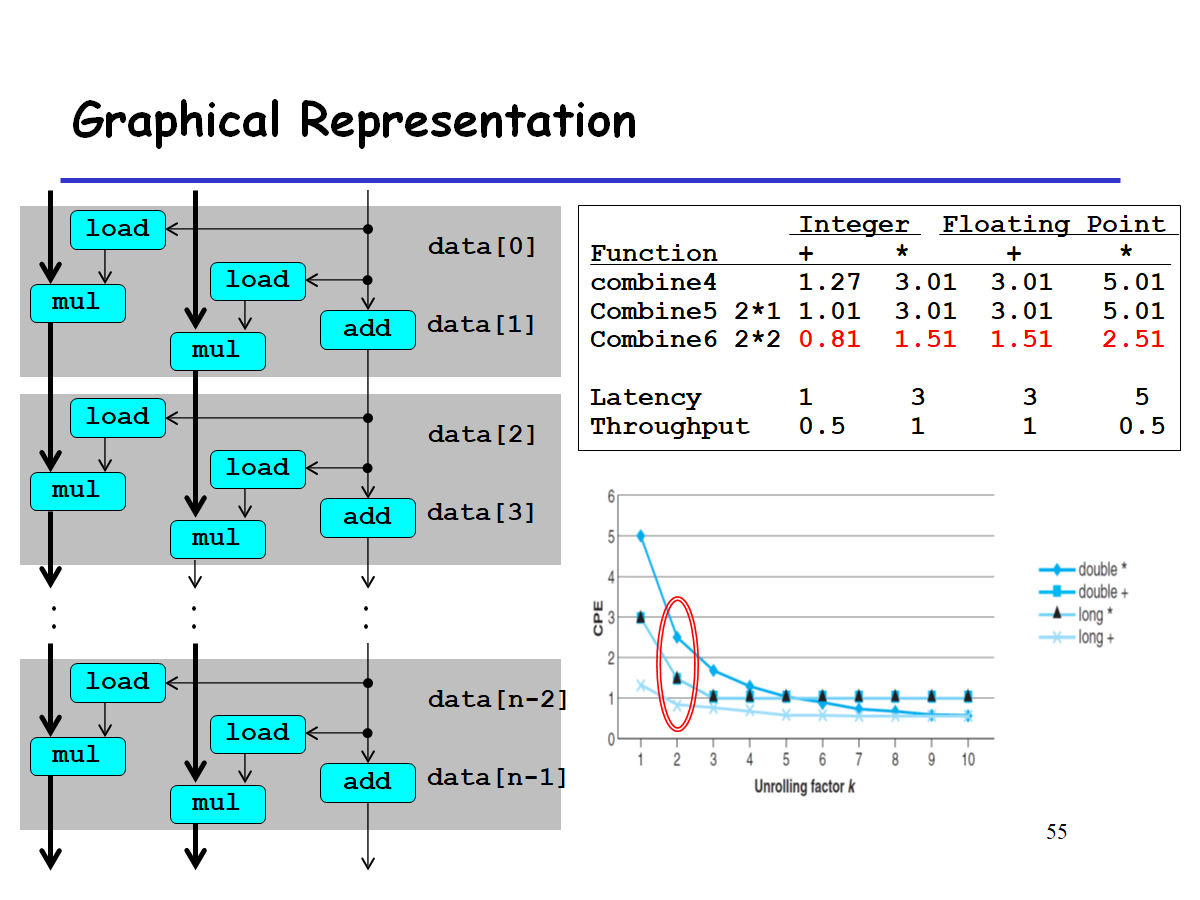
当有多个循环时,可简化为如下:
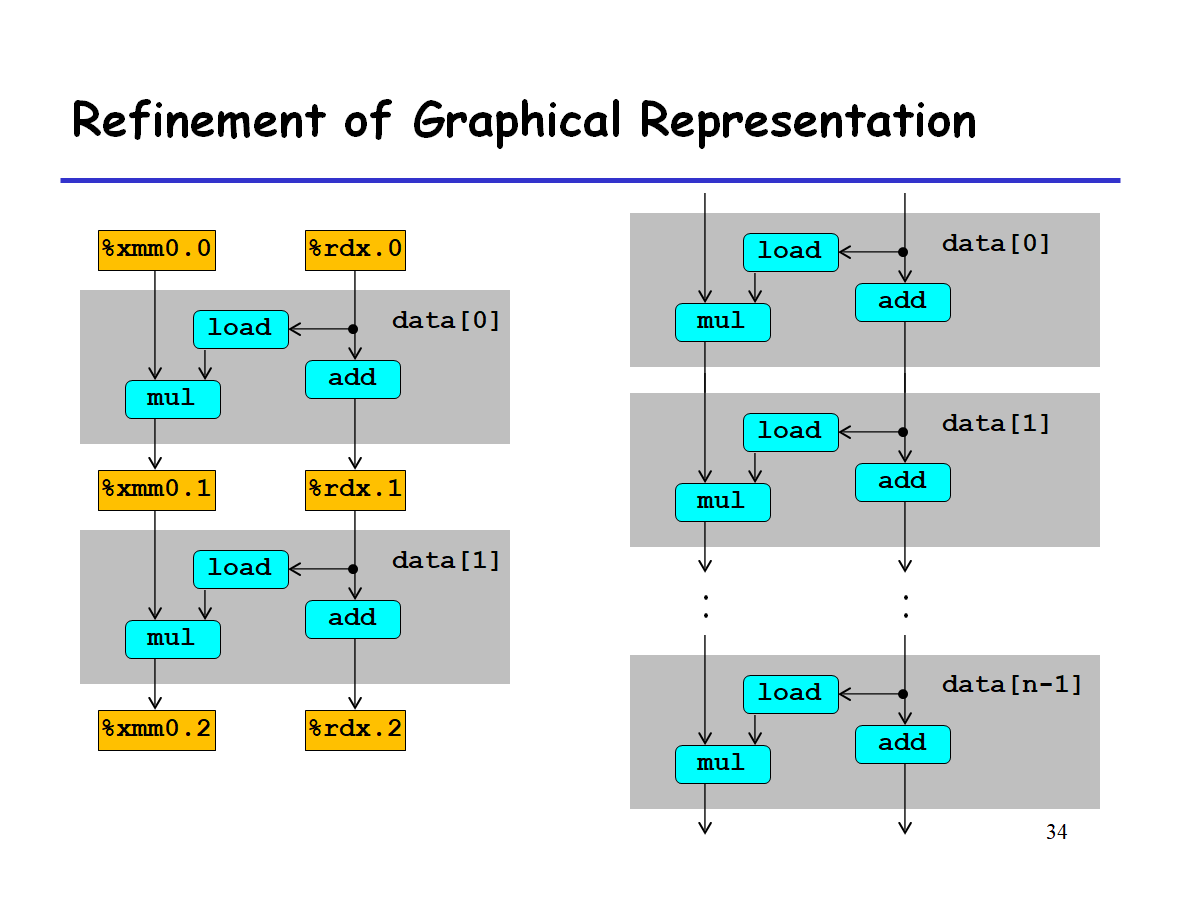
分析
上图中有两条数据依赖的路径:
- x(%xmm)的更新,mul操作
- i(%rdx)的更新,add操作
关键路径 :决定着所有操作时延上线的道路。
- 浮点数乘法的时延为5
- 整数加法的时延为1
// 核心问题抽象
for(i = 0; i < length; i++)x = x * data[i];
所以一次循环最少也需要5个clock才能执行完,所以理论上combine4的latency就是5.
我们回顾一下combine4优化的结果:

正符合理论结果!
CPE正好就是微操作的latency.

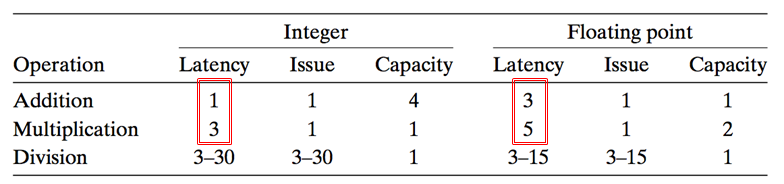
当然细心的读者可能发现了,为什么整数乘法的结果是1.27而不是1呢?
这种数据流表示只是为latency提供了一个下限。实际情况更为复杂:
- 有多少功能模块可用。比方说unit0和unit1不光执行整数加法,还执行浮点运算、除法运算等等。所以并不是每一个clock都能加载整数加法运算。
- 功能模块传递的数据量也是有上限的。
促进并发(parallelism)
以上我们虽然了解了限制运行速度的底层原理,但还是无法进一步优化代码。可以注意到Issue的值都为1. 我们可以将操作的时延降到1或更低吗?
这就需要将多条指令同时执行,而不是只能一个等着另一个。
n*1 循环展开
首先来看一下这个代码:
void combine5(vec_ptr v, int *dest)
{int i;int length = vec_length(v);int limit = length - 1;data_t *data = get_vec_start(v);data_t acc = IDENT;/* combine 2 elements at a time */for (i = 0; i < limit; i+=2)acc = acc OPER data[i] OPER data[i+1];/* finish any remaining elements */for (; i < length; i++)acc = acc OPER data[i];*dest = acc ;
}
在for循环中一次执行了两次操作。 这种方法叫做 Loop Unrolling , 译为 循环展开 . 在本例中执行2个运算,有1个独立的data链,所以叫做 2*1循环展开.
3*1循环展开也类似,作出相应的数据流图:
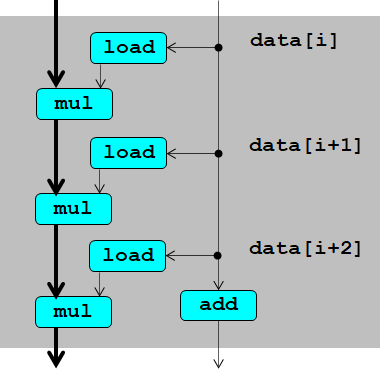
load操作不存在依赖关系(因为load不会改变data数组的内容),所以肯定可以并发运行。
关键路径:
- integer add: 时延为1
- double mul: 时延为5
图中加黑的是关键路径,可见虽然做了循环展开,latency bound仍然不变,平均执行一次操作仍需要5个cycles.
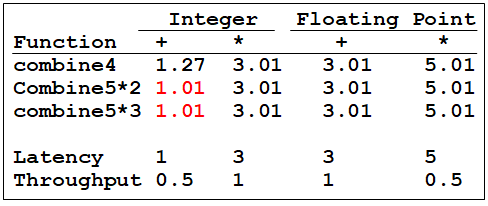
我们看到对于整数加法,CPE 有所改进,得到的延迟界限为 1.00。会有这样的结果 是得益于减少了循环开销操作。
但是其它情况并没有改良。
n*n循环展开
要想进一步降低时延,就要让两次mul操作之间不存在数据依赖,也就是让两次mul分开并发地执行。
见代码:
void combine6(vec_ptr v, int *dest)
{int i;int length = vec_length(v), limit = length-1;data_t *data = get_vec_start(v);data_t acc0 = IDENT, acc1 = IDENT;/* combine 2 elements at a time */for (i = 0; i < limit; i+=2){acc0 = acc0 OPER data[i];acc1 = acc1 OPER data[i+1];}/* finish any remaining elements */for (; i < length; i++)acc0 = acc0 OPER data[i];*dest = acc0 OPER acc1;
}
上面用了两个变量acc0, acc1分别来存储data[i] & data[i+1] 的运算结果。等到循环结束后再合并。这样两个循环内的乘法不存在 data dependency.
一次循环有两次操作,有2个独立的操作,所以是 2*2循环展开。

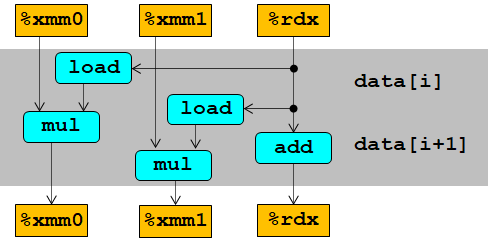
我们成功突破了时延的下限!
除了整数加法以外,其余操作都降低了一般的时延。
那么优化的极限是什么呢?
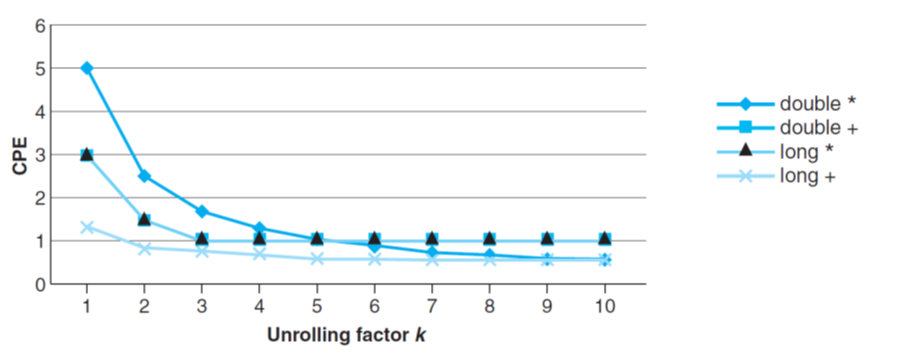
吞吐量界限(Throughout)

注意到Capacity, 而这正是处理单元的数量。理论上,随着循环展开数量的不断增加,操作的时延应该会不断逼近Issue. 而如果有两个处理单元的话,那么1个lock里就能执行两个操作,这使得时延变为0.5!而最优的时延值就是 Throughout.
不同的运算结合
void combine7(vec_ptr v, int *dest)
{int i;int length = vec_length(v), limit = length-1;data_t *data = get_vec_start(v);data_t acc = IDENT;/* combine 2 elements at a time */for (i = 0; i < limit; i+=2){acc = acc OPER (data[i] OPER data[i+1]);}/* finish any remaining elements */for (; i < length; i++)acc = acc OPER data[i];*dest = acc ;
}
这个函数和combine5的唯一区别就是这一句:
acc = acc OPER (data[i] OPER data[i+1]);
这使得两个乘法不存在数据依赖:
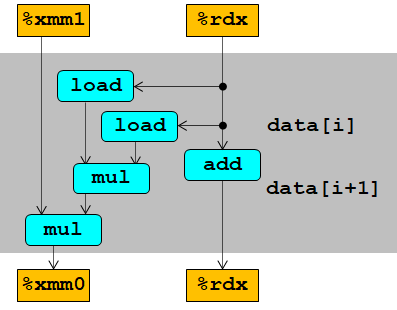

优化的限制因素
寄存器溢出
当寄存器不够用时,会用栈作为存储。
所以过多的循环展开反而导致速度下降。
分支预测
由于追求最高的效率,所以远在分支预测的结果出来前,就要加载下面更多的操作进行执行。所以一旦发现预测错误,就要撤销所有已经做的操作。
一般来说,Core i7 芯片由于一次预测错误将导致约19个时钟周期。
不过正常来说,分支预测都不位于关键路径上,不用特别担心。
不过下面是一个很明显的栗子,显示了预测错误惩罚的结果:

)


教程)






——构建高效数字化商业新生态)








