sklearn 笔记 metrics

1 分类

1.1 accuracy_score 分类准确率得分

在多标签分类中，此函数计算子集准确率：y_pred的标签集必须与 y_true 中的相应标签集完全匹配。

1.1.1 参数

y_true	真实（正确）标签
y_pred	由分类器返回的预测标签
normalize	默认为 True，返回正确分类的样本比例如果为 False，返回正确分类的样本数量
sample_weight	样本权重

二元分类中，等同于 jaccard_score

1.1.2 举例

from sklearn.metrics import accuracy_scorey_pred = [0, 2, 1, 3]
y_true = [0, 1, 2, 3]
accuracy_score(y_true, y_pred)
#0.5accuracy_score(y_true, y_pred, normalize=False)
#2

1.2 balanced_accuracy_score 计算平衡准确率

平衡准确率用于二元和多类分类问题中处理数据不平衡的情况。它定义为每个类别上获得的召回率的平均值。

当 adjusted=False 时，最佳值为 1，最差值为 0

sklearn.metrics.balanced_accuracy_score(y_true, y_pred, *, sample_weight=None, adjusted=False)

1.2.1 参数

y_true	真实（正确）的目标值
y_pred	由分类器返回的预估目标值
sample_weight	样本权重
adjusted	当为真时，结果会进行机会调整，使随机性能得分为 0，而完美性能保持得分为 1

1.2.2 举例

from sklearn.metrics import balanced_accuracy_score
y_true = [0, 1, 0, 0, 1, 0]
y_pred = [0, 1, 0, 0, 0, 1]
balanced_accuracy_score(y_true, y_pred),accuracy_score(y_true, y_pred)
#(0.625, 0.6666666666666666)'''
3/4+1/2=0.625
'''

1.3 top_k_accuracy_scoreTop-k 准确率分类得分

计算正确标签位于预测（按预测得分排序）的前 k 个标签中的次数

sklearn.metrics.top_k_accuracy_score(y_true, y_score, *, k=2, normalize=True, sample_weight=None, labels=None)

1.3.1 参数

y_true	真实（正确）的目标值
y_pred	由分类器返回的预估目标值
k	topk的k
normalize	默认为 True，返回正确分类的样本比例如果为 False，返回正确分类的样本数量
sample_weight	样本权重

1.3.2 举例

import numpy as np
from sklearn.metrics import top_k_accuracy_score
y_true = np.array([0, 1, 2, 2])
y_score = np.array([[0.5, 0.2, 0.2],  # 0 is in top 2[0.3, 0.4, 0.2],  # 1 is in top 2[0.2, 0.4, 0.3],  # 2 is in top 2[0.7, 0.2, 0.1]]) # 2 isn't in top 2
top_k_accuracy_score(y_true, y_score, k=2)
#0.75

1.4 f1_score F1 分数

sklearn.metrics.f1_score(y_true, y_pred, *, labels=None, pos_label=1, average='binary', sample_weight=None, zero_division='warn')

1.4.1 参数

y_true	真实（正确）的目标值
y_pred	由分类器返回的预估目标值
labels	当 `average` != 'binary' 时包括的标签集，以及 `average` 为 None 时的标签顺序。可以排除labels数据中存在的标签，例如在多类分类中可视为被排除的“负类” 默认情况下，labels=None，即使用 y_true 和 y_pred 中的所有标签，按排序顺序
pos_label	如果 `average='binary'` 且数据为二元，则报告该类对于多类或多标签目标，设置 `labels=[pos_label]` 并且 `average` != 'binary' 来仅报告一个标签的指标
average	这是对多类/多标签目标必需的。如果为 None，则返回每个类的分数。否则，这决定了对数据执行的平均类型： 'binary'：仅报告由 `pos_label` 指定的类的结果 'micro'：通过计算总的真正例、假负例和假正例来全局计算指标 'macro'：为每个标签计算指标，并找到它们的无权重平均。这不考虑标签不平衡。 'weighted'：为每个标签计算指标，并根据支持度（每个标签的真实实例数）找到它们的加权平均 'samples'：为每个实例计算指标，并找到它们的平均
sample_weight	样本权重
zero_division	当发生零除法时返回的值，即所有预测和标签都是负的情况

1.4.2 举例

import numpy as np
from sklearn.metrics import f1_score
y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0, 0, 1]
f1_score(y_true, y_pred, average='macro')
#0.26666666666666666
f1_score(y_true, y_pred, average='micro')
#0.3333333333333333
f1_score(y_true, y_pred, average='weighted')
#0.26666666666666666
f1_score(y_true, y_pred, average=None)
#array([0.8, 0. , 0. ])

这个是怎么算出来的呢？

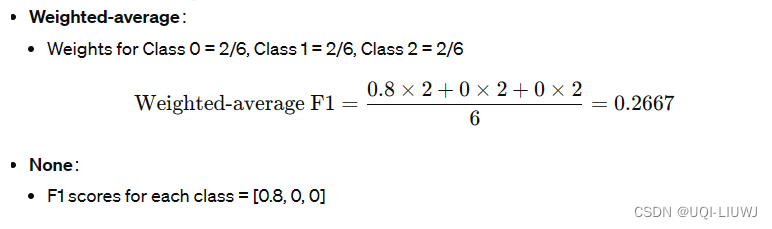
1.5 precision_score & recall_score

参数和用法和f1_score一致，就不多说了

1.6 jaccard_score

参数和f1_score一致

1.6 log loss 交叉熵损失

对于具有真实标签 y 和概率估计 p 的单个样本，log loss 为：

1.6.1 参数

y_true	真实（正确）的目标值
y_pred	由分类器返回的预估目标值
eps	Log loss 在 p=0 或 p=1 时未定义，因此概率被剪辑到 max(eps, min(1 - eps, p)) 默认值取决于 y_pred 的数据类型
normalize	bool，默认为 True则返回每个样本的平均损失否则，返回每个样本损失的总和。
sample_weight	样本权重
labels	labels array-like，默认为 None 如果未提供，将从 y_true 推断出标签。提取出所有unique的label，然后排序？如果 labels 为 None 且 y_pred 的形状为 (n_samples,)，则假定标签为二进制，并从 y_true 中推断出来

1.6.2 举例

from sklearn.metrics import log_loss
log_loss(["spam", "ham", "ham", "spam"],[[.1, .9], [.9, .1], [.8, .2], [.35, .65]])
#0.21616187468057912

怎么算出来的呢？

首先，这里没有提供labels，所以需要自己从y_true中infer出来，这边有两个不同的label：“ham"和”spam"，通过排序，可以知道每一个二元组中的第一个元素是ham的概率，第二个元素是spam的概率’‘

import math# 计算第一个样本的 log loss
loss1 = -(1 * math.log(0.9) + 0 * math.log(0.1))# 计算第二个样本的 log loss
loss2 = -(0 * math.log(0.1) + 1 * math.log(0.9))# 计算第三个样本的 log loss
loss3 = -(0 * math.log(0.2) + 1 * math.log(0.8))# 计算第四个样本的 log loss
loss4 = -(1 * math.log(0.65) + 0 * math.log(0.35))# 计算平均 log loss
average_log_loss = (loss1 + loss2 + loss3 + loss4) / 4
average_log_loss
#0.21616187468057912

2 聚类

2.1 调整互信息

sklearn.metrics.adjusted_mutual_info_score(labels_true, labels_pred, *, average_method='arithmetic')

调整互信息（AMI，Adjusted Mutual Information）是互信息（MI，Mutual Information）的一个改进版本，用于考虑随机性的影响。
互信息通常会随着聚类数量的增加而增加，无论是否实际上共享了更多的信息。
AMI通过修正互信息，排除了这种数量上的偏差。
对于两个聚类 U 和 V，AMI的计算公式如下：

2.1.1 参数

y_true

真实（正确）的目标值

y_pred

由分类器返回的预估目标值

average_method

{‘min’, ‘geometric’, ‘arithmetic’, ‘max’}，默认为 ‘arithmetic’

计算分母中规范化因子的方法

2.1.2 举例

from sklearn.metrics import adjusted_mutual_info_score
labels_true = [0, 0, 1, 1, 2, 2]
labels_pred = [0, 0, 1, 2, 2, 2]
ami_score = adjusted_mutual_info_score(labels_true, labels_pred)
print("Adjusted Mutual Information (AMI) score:", ami_score)
#Adjusted Mutual Information (AMI) score: 0.5023607027202738

3 回归

3.1 max_error

sklearn.metrics.max_error(y_true, y_pred)

y_true	真实（正确）的目标值
y_pred	由分类器返回的预估目标值

from sklearn.metrics import max_error
y_true = [3, 2, 17, 1]
y_pred = [4, 2, 7, 1]
max_error(y_true, y_pred)
#10

3.2 mean_absolute_error

sklearn.metrics.mean_absolute_error(y_true, y_pred, *, sample_weight=None, multioutput='uniform_average')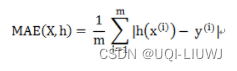

3.2.1 参数

y_true	真实（正确）的目标值
y_pred	由分类器返回的预估目标值
sample_weight	样本权重
multioutput	定义多输出值的聚合方式 ‘raw_values’：在多输出输入的情况下，返回每个输出的完整误差集。 ‘uniform_average’：所有输出的误差将以均匀权重进行平均。若为 array-like 值，则定义用于平均误差的权重

3.2.2 举例

from sklearn.metrics import mean_absolute_error
y_true = [0.5, -1, 7]
y_pred = [0, -1, 8]
mean_absolute_error(y_true, y_pred)
#0.5y_true = [[0.5, 1], [-1, 1], [7, -6]]
y_pred = [[0, 2], [-1, 2], [8, -5]]
mean_absolute_error(y_true, y_pred, multioutput='raw_values')
#array([0.5, 1. ])mean_absolute_error(y_true, y_pred)
#0.75
#上式两个取平均mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7])
#0.85
#0.5*0.3+1*0.7

3.3mean_squared_error

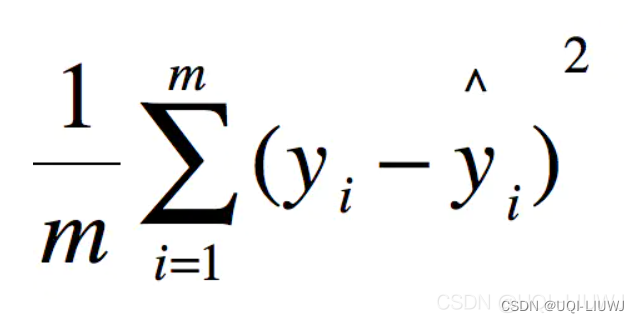
sklearn.metrics.mean_squared_error(y_true, y_pred, *, sample_weight=None, multioutput='uniform_average', squared='deprecated')

y_true	真实（正确）的目标值
y_pred	由分类器返回的预估目标值
sample_weight	样本权重
multioutput	定义多输出值的聚合方式 ‘raw_values’：在多输出输入的情况下，返回每个输出的完整误差集。 ‘uniform_average’：所有输出的误差将以均匀权重进行平均。若为 array-like 值，则定义用于平均误差的权重
squared	如果为True，就是MSE；如果为False，就是RMSE

3.4 root_mean_squared_error

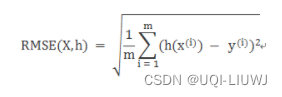
y_true	真实（正确）的目标值
y_pred	由分类器返回的预估目标值
sample_weight	样本权重
multioutput	定义多输出值的聚合方式 ‘raw_values’：在多输出输入的情况下，返回每个输出的完整误差集。 ‘uniform_average’：所有输出的误差将以均匀权重进行平均。若为 array-like 值，则定义用于平均误差的权重

3.5mean_squared_log_error

sklearn.metrics.mean_squared_log_error(y_true,     y_pred, *, sample_weight=None, multioutput='uniform_average', squared='deprecated')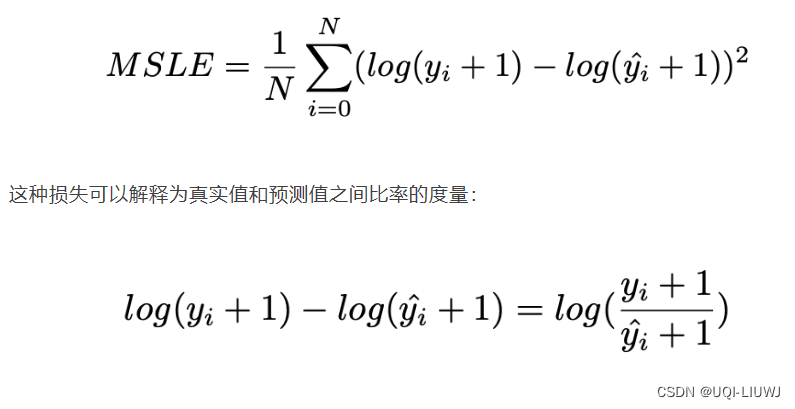

y_true	真实（正确）的目标值
y_pred	由分类器返回的预估目标值
sample_weight	样本权重
multioutput	定义多输出值的聚合方式 ‘raw_values’：在多输出输入的情况下，返回每个输出的完整误差集。 ‘uniform_average’：所有输出的误差将以均匀权重进行平均。若为 array-like 值，则定义用于平均误差的权重
squared	如果为True，就是MSLE；如果为False，就是RMSLE

3.6 root_mean_squared_log_error

root_mean_squared_log_error(y_true, y_pred, *, sample_weight=None, multioutput='uniform_average')

y_true	真实（正确）的目标值
y_pred	由分类器返回的预估目标值
sample_weight	样本权重
multioutput	定义多输出值的聚合方式 ‘raw_values’：在多输出输入的情况下，返回每个输出的完整误差集。 ‘uniform_average’：所有输出的误差将以均匀权重进行平均。若为 array-like 值，则定义用于平均误差的权重

3.7 median_absolute_error

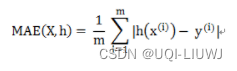
sklearn.metrics.median_absolute_error(y_true, y_pred, *, multioutput='uniform_average', sample_weight=None)

y_true	真实（正确）的目标值
y_pred	由分类器返回的预估目标值
sample_weight	样本权重
multioutput	定义多输出值的聚合方式 ‘raw_values’：在多输出输入的情况下，返回每个输出的完整误差集。 ‘uniform_average’：所有输出的误差将以均匀权重进行平均。若为 array-like 值，则定义用于平均误差的权重

3.8 median_absolute_error

sklearn.metrics.median_absolute_error(y_true, y_pred, *, multioutput='uniform_average', sample_weight=None)

absolute error的中位数

y_true	真实（正确）的目标值
y_pred	由分类器返回的预估目标值
sample_weight	样本权重
multioutput	定义多输出值的聚合方式 ‘raw_values’：在多输出输入的情况下，返回每个输出的完整误差集。 ‘uniform_average’：所有输出的误差将以均匀权重进行平均。若为 array-like 值，则定义用于平均误差的权重

3.9 mean_absolute_percentage_error

sklearn.metrics.mean_absolute_percentage_error(y_true, y_pred, *,     sample_weight=None, multioutput='uniform_average')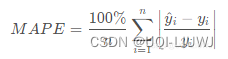

y_true	真实（正确）的目标值
y_pred	由分类器返回的预估目标值
sample_weight	样本权重
multioutput	定义多输出值的聚合方式 ‘raw_values’：在多输出输入的情况下，返回每个输出的完整误差集。 ‘uniform_average’：所有输出的误差将以均匀权重进行平均。若为 array-like 值，则定义用于平均误差的权重