
送给大家一句话:
既然已经做出了选择,最好还是先假定自己是对的。焦虑未来和后悔过去,只经历一个就够了。 – 张寒寺 《不正常人类症候群》
☆ミヾ(∇≦((ヾ(≧∇≦)〃))≧∇)ノ彡☆
☆ミヾ(∇≦((ヾ(≧∇≦)〃))≧∇)ノ彡☆
☆ミヾ(∇≦((ヾ(≧∇≦)〃))≧∇)ノ彡☆
前缀和入门
- 1 前言
- 1.1 算法步骤
- 1.2 使用场景
- 1.3 时间复杂度分析
- 1.4 空间复杂度分析
- 2 牛客 DP35 【模板】二维前缀和
- 题目描述
- 算法思路
- 3 牛客 DP35 【模板】二维前缀和
- 题目描述
- 算法思路
- Leetcode 724. 寻找数组的中心下标
- 题目描述
- 算法思路
- Leetcode 238. 除自身以外数组的乘积
- 题目描述
- 算法思路
- Thanks♪(・ω・)ノ谢谢阅读!!!
- 下一篇文章见!!!
1 前言
今天我学习了一个新算法:前缀和算法。
前缀和算法是一种高效处理数组区间和查询问题的算法。它的核心思想是在 O(n) 的时间复杂度内对输入数组进行预处理,从而使得后续每次查询数组中任意区间内元素和的时间复杂度降低到 O(1)。
1.1 算法步骤
- 初始化前缀和数组:创建一个新数组 dp,一般多开一位。
- 计算前缀和:遍历原数组 A,根据题目更新状态。
- 查询区间和:更加区间得到答案。
1.2 使用场景
- 频繁区间和查询:当需要对一个数组进行多次区间和查询时,前缀和可以大幅提高查询效率。
- 动态数据更新:在某些情况下,数组中的元素可能会动态更新,前缀和也能有效处理这种情况下的区间和查询。
- 多维数组处理:前缀和可以扩展到多维数组,用于处理多维数据区间和的问题。
1.3 时间复杂度分析
- 预处理时间复杂度:O(n),其中 n 是原数组 A 的长度。
- 查询时间复杂度:O(1),对于每次区间和查询。
1.4 空间复杂度分析
- 空间复杂度:O(n),用于存储前缀和数组 dp。
前缀和算法在处理数组区间和问题时非常高效,适用于需要频繁查询和高效处理大量数据的场景。通过前缀和的预处理,可以显著减少计算成本,提高程序的运行效率,也就是 空间换时间。
2 牛客 DP35 【模板】二维前缀和
上链接!!! DP34 一维前缀和
题目描述

根据题目描述,我们大概知道我们是求一个区间上的和。题目很好理解奥,接下来我们就来通过这道题来入门前缀和算法!!!
算法思路
首先最好想的就是暴力算法,求指定区间的和那么直接暴力求不就可以了?!但是毋庸置疑的是这样一定一定会超时,毕竟是O(n^2)的暴力算法。
那么来看前缀和算法,这是一个解决这个问题的优秀算法。前缀和的思想很简单,就是对数组进行一遍预处理,得到每个数组位置之前所有数的和,然后在通过减法求得数据。
- 创建一个大小为 n + 1 的数组(大小为 n + 1可以避免一些边界情况)
- 从 下标 1 开始读入数据
- 创建一个大小为 n + 1 的 dp 数组
- 从 下标 1 开始预处理数据
- 得到答案
#include <iostream>
#include <vector>
using namespace std;int main() {int n , q;cin >> n >> q;//读入数据vector<long long > nums(n + 1);for(int i = 1 ; i < n + 1 ; i++ ){cin >> nums[i];}//预处理数据vector<long long > sum(n + 1);for(int i = 1 ; i < nums.size() ;i++ ){//i 位置的和等于 i - 1 位置的和 加上 i 位置的值//如果数组大小为n 那 i 从 0开始 那么就会读入 nums[-1]就会报错sum[i] = sum[i - 1] + nums[i];}//得出结果while(q--){int n1 , n2;cin >> n1 >> n2;cout <<sum[n2] - sum[n1 - 1] << endl;}return 0;
}
这样提交:过啦!!!
这里有点像动态规划奥
3 牛客 DP35 【模板】二维前缀和
家人们跟上节奏!!!DP35 二维前缀和
题目描述

根据题目描述,这道题是刚才一维的升级版,我们需要计算一个指定矩阵的和。那么依然使用的是前缀和来进行预处理。这道题就要注意细节处理了
算法思路
首先最好想的就是暴力算法,求指定矩阵的和那么直接暴力求不就可以了?!但是毋庸置疑的是这样一定一定会超时,O(n^3)的暴力算法啊。
那么来看前缀和算法,这是一个解决这个问题的优秀算法。前缀和的思想很简单,就是对数组进行一遍预处理,得到每个数组位置之前所有数的和,然后在通过减法求得数据。
- 创建一个大小为 (n + 1) *( n + 1) 的矩阵(大小为 n + 1可以避免一些边界情况)
- 从 坐标(1,1) 开始读入数据
- 创建一个大小为 (n + 1) *( n + 1) 的 dp 矩阵
- 从 坐标(1,1)开始预处理数据
- 得到答案
这里的预处理就有说法了,这和线性的数组不一样,我们做一个图就可以很好理解预处理然后进行:
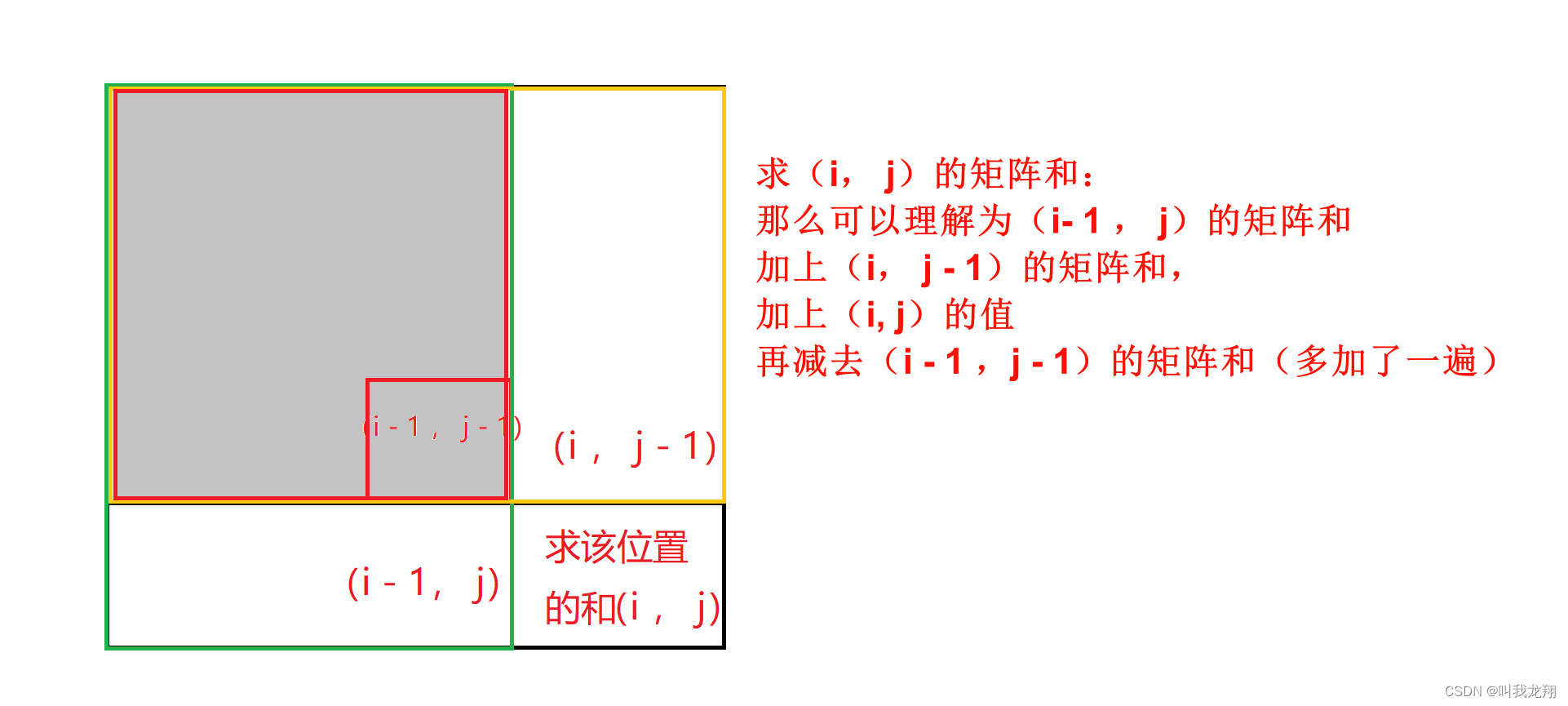
求(i,j)的矩阵和:
可以理解为(i-1,j)的矩阵和 加上 (i,j-1)的矩阵和,加上(i,j)的值再减去(i-1,j-1)的矩阵和(因为多加了一遍)
这样就可以进行预处理了:
然后我们还需要如何得到答案:
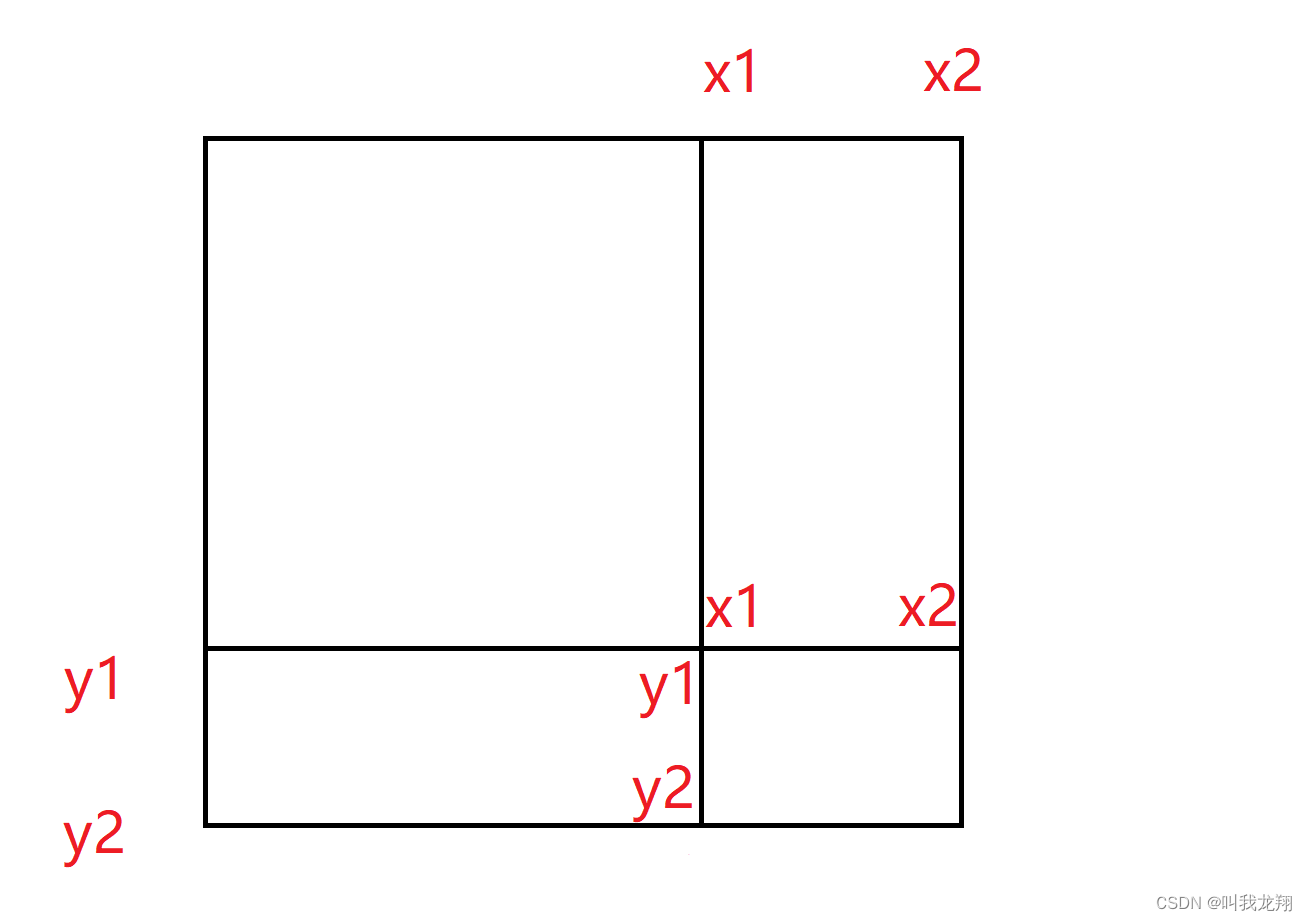
我们想要求以 (x1, y1) 为左上角 , (x2,y2) 为右下角的子矩阵的和。
可以通过 (x2,y2) 矩阵和 减去(x2 , y1 - 1)矩阵和 减去(x1 - 1 , y2)矩阵和 加上(x1 - 1, y1 - 1)的矩阵和(因为多减了一遍)
#include <iostream>
#include <vector>
#define int long longusing namespace std;signed main() {int n , m ,q;cin >> n >> m >> q;//创建二维数组 匿名对象构造vector<vector<int>> nums(n + 1 , vector<int>(m + 1));for(int i = 1 ; i <= n ; i++ )for(int j = 1 ; j <= m ; j++)cin>>nums[i][j];//进行前缀和计算vector<vector<int>> dp(n + 1 , vector<int>(m + 1));for(int i = 1 ; i <= n ; i++ )for(int j = 1 ; j <= m ; j++)dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + nums[i][j];int x1 , x2 , y1 ,y2;while(q--){cin >> x1 >> y1 >> x2 >>y2;cout << dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1] << endl;}return 0;
}
提交过啦!!!
Leetcode 724. 寻找数组的中心下标
跟上节奏:724. 寻找数组的中心下标
题目描述

这道题可谓是一维前缀和的变形了,我们来秒杀这个题目
算法思路
我们先进行一下前缀和的预处理,然后根据条件判断即可:
class Solution {
public:int pivotIndex(vector<int>& nums) {//预处理vector<int> dp(nums.size() + 1);for(int i = 1 ; i <= nums.size() ;i++){dp[i] = dp[i - 1] + nums[i - 1];}int ans = -1;//根据题目要求求得即可for(int i = 0 ; i < nums.size() ;i++){if(dp[i] == dp[nums.size()] - dp [i + 1] ){ans = i ;break;}}return ans;}
};
提交过啦!!!
Leetcode 238. 除自身以外数组的乘积
最后一道:238. 除自身以外数组的乘积
题目描述

注意到题目要求,我们看来是要使用前缀和来解决问题了。
算法思路
这道题的难点在于不能不能使用除法,而且还要进行O(n)的算法
那么如何进行呢???
- 很简单,我们在创建一个前缀乘积数组与一个后缀乘积数组,分开进行预处理即可。
- 然后按照对应位置,通过n - 1 的前缀乘积与 n + 1 的后缀乘积相乘 得到 除自身以外数组的乘积,就可以了。
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> dpfront(n + 1);vector<int> dpback(n + 1);//细节处理,不能为0哦!!!dpfront[0] = 1;dpback[n] = 1;//预处理for(int i = 1 ; i <= n ; i++){ //一次处理两个数组,提高效率dpfront[i] = dpfront[i - 1] * nums[i - 1];dpback[n - i] = dpback[n - i + 1] * nums[n - i];}//得到答案for(int i = 0 ; i < n ; i++){nums[i] = dpfront[i] * dpback[i + 1];}return nums;}
};
提交:过啦!!!




)


)










