在之前的文章中,我们了解我们的机器学习,了解我们spark机器学习中的特征提取和我们的tf-idf,word2vec算法。想了解的朋友可以查看这篇文章。同时,希望我的文章能帮助到你,如果觉得我的文章写的不错,请留下你宝贵的点赞,谢谢。
Spark-机器学习(2)特征工程之特征提取-CSDN博客文章浏览阅读2k次,点赞54次,收藏36次。今天的文章,我会带着大家一起了解我们的特征提取和我们的tf-idf,word2vec算法。希望大家能有所收获。同时,本篇文章为个人spark免费专栏的系列文章,有兴趣的可以收藏关注一下,谢谢。同时,希望我的文章能帮助到每一个正在学习的你们。也欢迎大家来我的文章下交流讨论,共同进步。https://blog.csdn.net/qq_49513817/article/details/137844271今天的文章,我们来学习我们回归中的线性回归,希望大家能有所收获。
目录
一、线性回归
什么是线性回归?
spark线性回归
二、示例代码
拓展-线性回归算法介绍及用法
1.算法
2.用法
一、线性回归
什么是线性回归?
 线性回归
线性回归
线性回归研究是一种统计学上分析的方法,旨在确定两种或两种以上变量间相互依赖的定量关系。这种关系通常用一个线性方程来表示,其中一个或多个自变量(也称为解释变量或特征)与因变量(也称为响应变量或目标)之间的关系被假定为线性。
在线性回归模型中,因变量被假设为自变量通过一个线性组合加上一个常数项(截距)以及一个误差项(随机扰动)来影响。这个线性组合中的系数,也被称为回归系数,反映了各自变量对因变量的影响程度和方向。
线性回归研究通常包括以下步骤:
-
数据收集:收集包含自变量和因变量的数据集。
-
模型建立:根据收集的数据,建立线性回归模型。
-
参数估计:使用最小二乘法等方法来估计模型中的参数(回归系数和截距)。最小二乘法通过最小化预测值与实际值之间的平方误差和来找到最佳拟合的回归系数。
-
模型检验:对模型的拟合效果进行检验,包括检验回归系数的显著性(如t检验)以及模型整体的拟合优度(如R²值)。
-
预测与解释:利用拟合好的模型进行预测,并解释各自变量对因变量的影响。
线性回归研究在多个领域都有广泛应用,如经济预测、市场营销、医学、社会科学等。它提供了一种量化变量间关系的方法,并能通过统计检验来评估这种关系的可靠性。然而,线性回归的前提假设(如线性关系、误差项的独立性等)需要在实际应用中进行检验,以确保模型的适用性。如果数据不满足这些假设,可能需要使用其他类型的回归模型,如多项式回归、逻辑回归等。
spark线性回归
Spark线性回归是Apache Spark框架中实现线性回归分析的一种功能。线性回归是利用线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。在Spark中,线性回归模型可以通过最小二乘法等优化算法来估计模型的参数,从而建立自变量和因变量之间的线性关系。
Spark支持多种线性回归方法,包括普通线性回归(LinearRegression)、加L1正则化的线性回归(LassoRegression)以及加L2正则化的线性回归(RidgeRegression)。这些方法提供了灵活性和鲁棒性,以适应不同的数据和分析需求。
通过Spark线性回归,用户可以处理大规模数据集,并利用分布式计算能力来加速模型的训练和预测过程。这使得线性回归在大数据场景下更加高效和实用。
Spark线性回归是一种利用Apache Spark框架进行线性回归分析的方法,旨在从大规模数据集中发现变量之间的线性关系,并为预测和决策提供支持。
二、示例代码
import org.apache.spark.{SparkConf, SparkContext}
import org.apache.spark.ml.regression.LinearRegression
import org.apache.spark.ml.feature.VectorAssembler
import org.apache.spark.ml.evaluation.RegressionEvaluator
import org.apache.spark.sql.SparkSession
object p4 {def main(args: Array[String]): Unit = {val conf = new SparkConf().setMaster("local").setAppName("ppp")val sc = new SparkContext(conf)val spark = SparkSession.builder().appName("SimpleLinearRegression").getOrCreate()import spark.implicits._// 假设这里有一些数据,例如:(1.0, 2.0, 3.0), (2.0, 3.0, 5.0), ...// 这里我们使用一些随机数据作为示例val data = sc.parallelize(Seq((1.0, 2.0, 3.0),(2.0, 3.0, 5.0),(3.0, 4.0, 7.0))).toDF("feature1", "feature2", "label")// 使用VectorAssembler将所有特征转换为一个特征向量val assembler = new VectorAssembler().setInputCols(Array("feature1", "feature2")).setOutputCol("features")val output = assembler.transform(data)// 分割数据集为训练集和测试集val Array(trainingData, testData) = output.randomSplit(Array(0.7, 0.3))// 创建线性回归模型val lr = new LinearRegression().setMaxIter(10).setRegParam(0.3).setElasticNetParam(0.8)// 在训练集上训练模型val lrModel = lr.fit(trainingData)// 在测试集上进行预测val predictions = lrModel.transform(testData)// 选择(预测值, 真实值)并计算测试误差val evaluator = new RegressionEvaluator().setLabelCol("label").setPredictionCol("prediction").setMetricName("mse")val mse = evaluator.evaluate(predictions)println(s"Root-mean-square error = $mse")}
}代码首先创建了一个SparkContext和一个SparkSession对象,然后创建了一个包含三个字段(feature1, feature2, label)的DataFrame,其中feature1和feature2是特征,label是目标变量。
然后,代码使用VectorAssembler将feature1和feature2合并成一个特征向量,接着将数据集分割为训练集和测试集。
接下来,代码创建了一个线性回归模型,设置了最大迭代次数、正则化参数和弹性网络混合参数,然后在训练集上训练了这个模型。
最后,代码在测试集上进行了预测,并使用RegressionEvaluator计算了均方误差(MSE)。
运行代码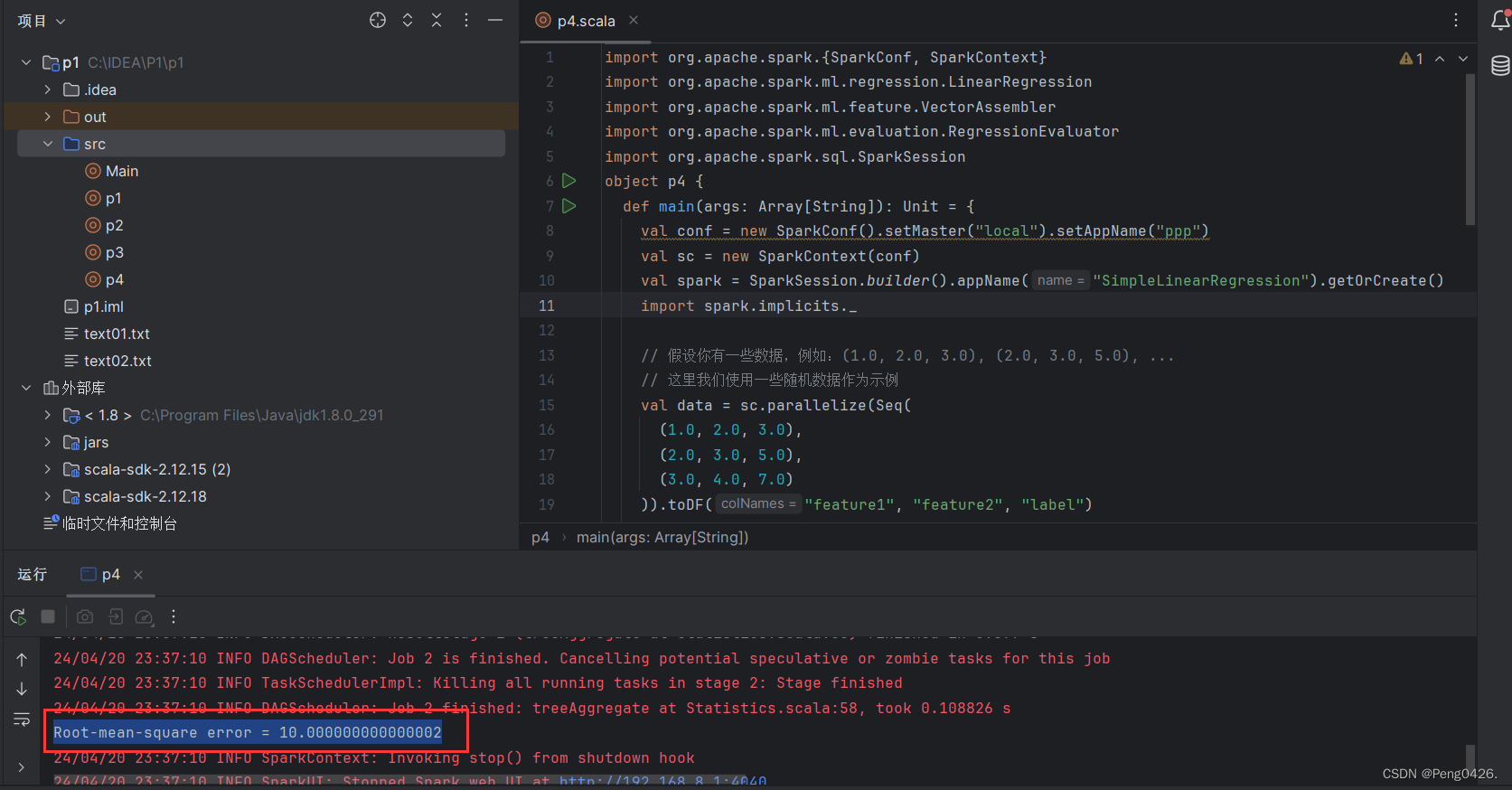
我们成功得到了我们的均方根误差(Root-mean-square Error,简称RMSE)
RMSE 的值越小,说明模型的预测性能越好,即模型的预测值与实际观测值之间的差异越小。相反,RMSE 的值越大,则模型的预测性能越差。
RMSE 对于大的误差非常敏感,因此它可以有效地揭示模型在预测大误差时的性能。
拓展-线性回归算法介绍及用法
1.算法
-
最小二乘法(Ordinary Least Squares)
- 描述:最基础的线性回归方法,通过最小化预测值与实际值之间的平方误差来求解回归系数。
- 特点:计算速度快,但当数据量大或特征多时可能不太稳定。
-
梯度下降法(Gradient Descent)
- 描述:通过迭代的方式逐步调整回归系数,以最小化损失函数。
- 变种:
- 批量梯度下降(Batch Gradient Descent):每次迭代使用所有数据点来更新系数。
- 随机梯度下降(Stochastic Gradient Descent):每次迭代只使用一个数据点来更新系数,速度更快,适用于大数据集。
- 特点:灵活,可以通过调整学习率和迭代次数来控制收敛速度和精度。
-
正则化方法
- 描述:为了防止过拟合,可以在损失函数中加入正则化项。
- 类型:
- Lasso回归(L1正则化):使用L1范数作为正则化项,有助于产生稀疏模型。
- Ridge回归(L2正则化):使用L2范数作为正则化项,有助于稳定模型。
- ElasticNet回归:结合L1和L2正则化,提供了更多的灵活性。
2.用法
| 方法/算法关键字 | 描述 | 使用场景 | 示例代码关键字/片段 |
|---|---|---|---|
| 最小二乘法 (Ordinary Least Squares) | 通过最小化预测值与实际值之间的平方误差来求解回归系数。 | 基础线性回归场景,当数据量和特征数量适中时。 | LinearRegression().fit(training) |
| 批量梯度下降 (Batch Gradient Descent) | 使用所有数据点来计算梯度并更新回归系数,每次迭代都会遍历整个数据集。 | 数据集较小,或需要精确求解的场景。 | LinearRegression().setMaxIter(10).setRegParam(0.3).fit(training) |
| 随机梯度下降 (Stochastic Gradient Descent) | 每次迭代只使用一个数据点来计算梯度并更新系数,适用于大数据集。 | 大规模数据集,需要快速迭代更新的场景。 | LinearRegression().setSolver("sgd").setMaxIter(100).fit(training) |
| Lasso回归 (L1正则化) | 在损失函数中加入L1正则化项,有助于产生稀疏模型,适用于特征选择。 | 需要进行特征选择,或希望模型具有稀疏性的场景。 | LinearRegression().setElasticNetParam(1.0).fit(training) |
| Ridge回归 (L2正则化) | 在损失函数中加入L2正则化项,有助于稳定模型,防止过拟合。 | 数据集存在噪声或特征间存在相关性,需要稳定模型的场景。 | LinearRegression().setRegParam(0.3).fit(training) |
| ElasticNet回归 | 结合L1和L2正则化,提供了更多的灵活性,可以根据数据和需求调整正则化强度。 | 需要平衡特征选择和模型稳定性的场景。 | LinearRegression().setElasticNetParam(0.8).fit(training) |

)

















