引言

我自认空间想象能力较差，所以当初学这个很吃力。希望现在再接触，能好点。

一、空间解析几何的理论

1.1 基本概念

1.向量 —— 既有大小，又有方向的量称为向量，常用从起点指向终点的带箭头的有向线段 $\overrightarrow{AB}$ 表示，或用带箭头的小写字母 $\overrightarrow{a}$ 。

向量的大小或长度称为向量的模，向量 $\overrightarrow{a}$ 的模记作 $|\overrightarrow{a}|$ 。特别地，模为 1 的向量称为单位向量，模为 0 的向量称为零向量，记作 $\overrightarrow{a}^0$ 。大小相等且方向相同的向量相等。

2.向量的坐标 —— 设 $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ 分别表示 $x, y, z$ 轴正向的单位向量，设向量 $\overrightarrow{a}$ 在三个坐标轴上的投影分别为 $a, b, c$ ，由向量的分解得 $\overrightarrow{a}=a\overrightarrow{i}+b\overrightarrow{j}+c\overrightarrow{k}=\{a,b,c\}$ ，称 ${a,b,c\}$ 为向量 $\overrightarrow{a}$ 的坐标。

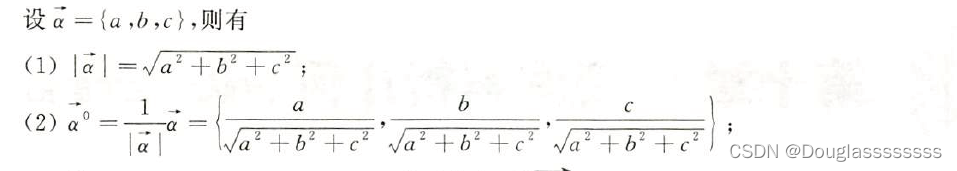
在这里插入图片描述

3.向量的方向角和方向余弦 —— 设 $\overrightarrow{a}=\{a,b,c\}$ 为非零向量，则 $\overrightarrow{a}$ 与 $x, y, z$ 轴正向的夹角，称为此向量的方向角，分别记为 $\alpha,\beta,\gamma$ ，称 $\cos\alpha,\cos\beta,\cos\gamma$ 为 $\overrightarrow{a}$ 的方向余弦。则 $\cos\alpha=\frac{a}{\sqrt{a^2+b^2+c^2}},\cos\beta=\frac{b}{\sqrt{a^2+b^2+c^2}},\cos\alpha=\frac{c}{\sqrt{a^2+b^2+c^2}}$ 显然，有 $\overrightarrow{a}^0=\{\cos\alpha,\cos\beta,\cos\gamma\}$ ， $\cos\alpha^2+\cos\beta^2+\cos\gamma^2=1$ 。

4.向量在一个轴（向量）上的投影 —— 设 $u$ 为一个数轴， $\overrightarrow{a}$ 为一个向量，过向量的起点 A 和终点 B 作 $u$ 轴的垂直面交 $u$ 轴于点 $A_1,B_1$ ，其在 $u$ 轴上的坐标分别为 $x_1,x_2$ ，称 $x_2-x_1$ 为向量 $\overrightarrow{a}$ 在 $u$ 轴上的投影，记为 $Prj_u\overrightarrow{a}=x_2-x_1$ ，且 $Prj_u\overrightarrow{a}=|\overrightarrow{a}|\cos(u,\overrightarrow{a})$ 。