深度优先遍历（DFS）是一种常用的树或图的遍历算法，它通过尽可能深地搜索树或图的分支，直到路径上的所有节点都被访问完毕，然后再回溯到上一层，继续搜索其他路径。在二叉树中，常见的深度优先遍历包括前序遍历、中序遍历和后序遍历。

1.算法原理

深度优先遍历算法的核心思想是通过递归或栈来实现，它遵循以下步骤：

1. 从根节点（或其他指定的起始节点）开始遍历。
2. 访问当前节点，并标记为已访问。
3. 递归地遍历当前节点的邻居节点，如果邻居节点未被访问，则重复步骤2。
4. 当所有邻居节点都被访问完毕或当前节点没有未访问的邻居节点时，回溯到上一层节点，继续遍历其他分支。

2. 常见的深度优先遍历方式

在二叉树中，常见的深度优先遍历方式有三种：

• 前序遍历（Preorder Traversal）：先访问根节点，然后递归地遍历左子树和右子树。
• 中序遍历（Inorder Traversal）：先递归地遍历左子树，然后访问根节点，最后递归地遍历右子树。
• 后序遍历（Postorder Traversal）：先递归地遍历左子树和右子树，然后访问根节点。

3. 代码实现

#include <iostream>
#include <stack>
using namespace std;// 定义二叉树节点结构体
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};// 前序遍历（递归版本）
void preorderTraversal(TreeNode* root) {if (root) {cout << root->val << " ";preorderTraversal(root->left);preorderTraversal(root->right);}
}// 中序遍历（递归版本）
void inorderTraversal(TreeNode* root) {if (root) {inorderTraversal(root->left);cout << root->val << " ";inorderTraversal(root->right);}
}// 后序遍历（递归版本）
void postorderTraversal(TreeNode* root) {if (root) {postorderTraversal(root->left);postorderTraversal(root->right);cout << root->val << " ";}
}int main() {// 构建示例二叉树//       1//      / \//     2   3//    / \//   4   5TreeNode* root = new TreeNode(1);root->left = new TreeNode(2);root->right = new TreeNode(3);root->left->left = new TreeNode(4);root->left->right = new TreeNode(5);cout << "前序遍历：";preorderTraversal(root);cout << endl;cout << "中序遍历：";inorderTraversal(root);cout << endl;cout << "后序遍历：";postorderTraversal(root);cout << endl;// 释放内存delete root->left->left;delete root->left->right;delete root->left;delete root->right;delete root;return 0;
}

应用：

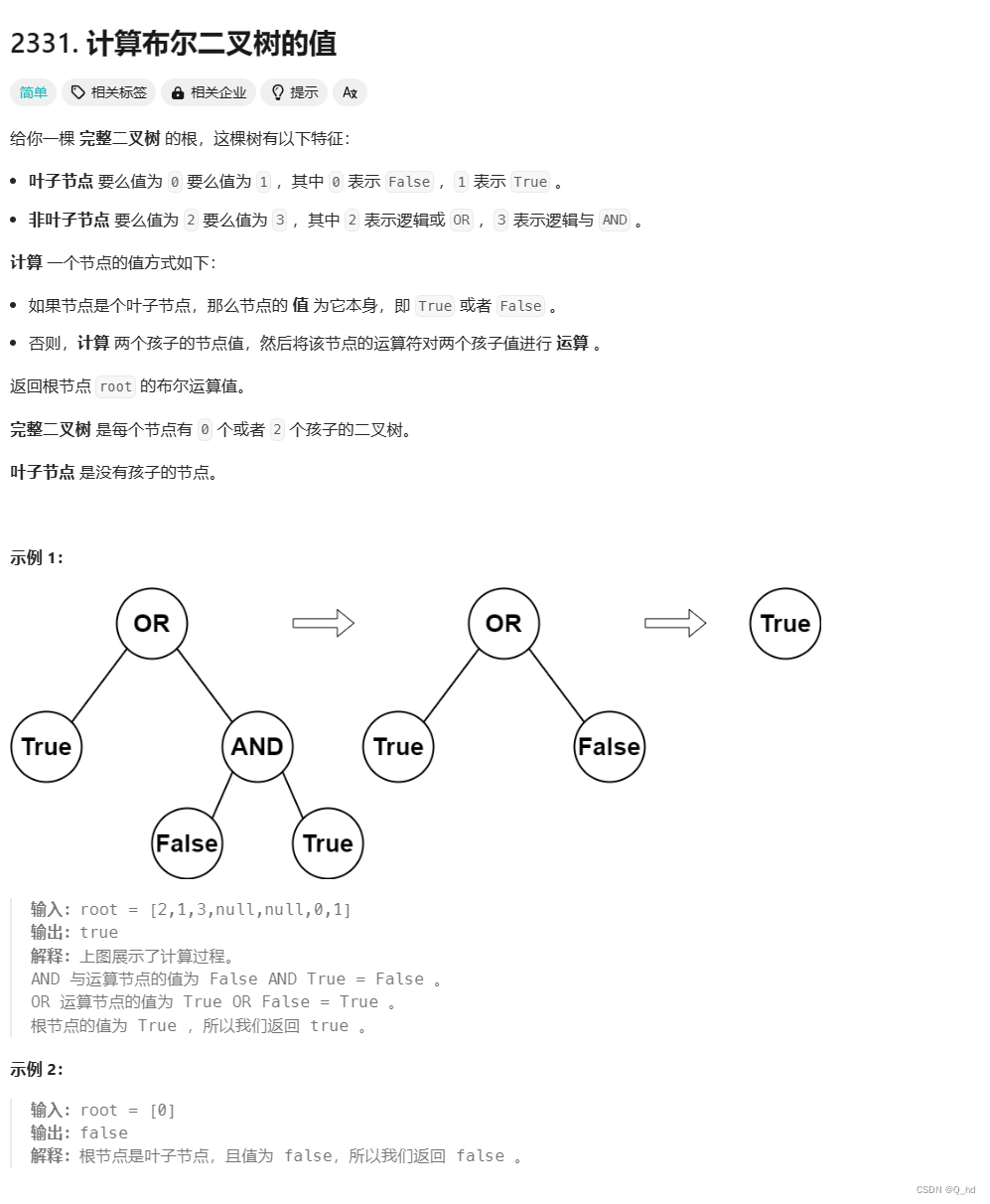
class Solution {
public:bool evaluateTree(TreeNode* root) {// 判断是否为叶子节点if (root->left == nullptr) return root->val == 0 ? false : true;//dfsbool left = evaluateTree(root->left);bool right = evaluateTree(root->right);return root->val == 2 ? left | right : left & right; }
};

总结

深度优先遍历是一种重要的遍历算法，对于理解树和图的结构及其应用具有重要意义。通过掌握深度优先遍历的原理和常见实现方式，能够更加深入地理解算法的本质，并能够应用于解决各种相关问题。