【前端面试3+1】16 TCP与UDP的区别、如何清除浮动、哪些原因造成阻塞页面渲染、【相同的树】

一、TCP与UDP的区别

TCP（Transmission Control Protocol）和UDP（User Datagram Protocol）是两种常用的网络传输协议，它们有以下几点区别：

1、连接性：

TCP是面向连接的协议，通信双方在传输数据之前需要建立连接，数据传输完毕后需要断开连接。
UDP是无连接的协议，通信双方之间在传输数据时不需要建立连接，数据包之间相互独立。

2、可靠性：

TCP提供可靠的数据传输，它通过序列号、确认应答、重传机制等来确保数据的完整性和可靠性。
UDP不提供数据传输的可靠性保证，数据包可能会丢失或乱序，应用程序需要自行处理数据的丢失或重传。

3、传输效率：

TCP的可靠性和连接管理会带来一定的开销，因此在传输效率上通常比UDP略低。
UDP没有连接管理和可靠性保证，传输效率较高，适用于实时性要求较高的应用场景。

4、应用场景：

TCP适用于需要可靠数据传输和顺序传输的应用，如文件传输、网页访问等。
UDP适用于实时性要求较高、数据量较小、允许数据丢失的应用，如音视频传输、在线游戏等。

二、如何清除浮动？

清除浮动是为了解决父元素包含浮动子元素时可能导致的高度塌陷或布局错乱的问题。

1、使用clearfix技巧：

在父元素上应用 clearfix 类，可以通过以下方式实现：
.clearfix::after {content: "";display: table;clear: both;
}
2、使用overflow属性：

在父元素上添加 overflow: hidden; 或 overflow: auto; 属性，可以触发 BFC（块级格式化上下文），从而清除浮动。

3、使用伪元素清除浮动：

在父元素上使用伪元素清除浮动，如下所示：
.parent::after {content: "";display: table;clear: both;
}
4、使用clear属性：

在父元素之后添加一个空元素，并为其应用 clear: both; 属性，也可以清除浮动。

5、使用父元素设置高度：

如果知道子元素的高度，可以在父元素上设置一个固定高度，也可以清除浮动。

三、哪些原因会造成阻塞页面的渲染？

以下是一些常见的原因：

1、CSS和JavaScript资源的加载：

        当浏览器解析HTML文档时，遇到外部CSS和JavaScript资源的引用时，会停止解析并开始下载这些资源。如果这些资源加载速度较慢或者有大量资源需要下载，会导致页面渲染被阻塞。

2、JavaScript的执行：

        JavaScript的执行会阻塞页面的渲染。特别是在页面底部加载的JavaScript文件，如果JavaScript代码执行时间过长，会延迟页面的呈现。

3、CSS和JavaScript的解析：

        如果CSS和JavaScript文件较大或者包含复杂的代码，会增加解析时间，从而影响页面的加载速度

4、DOM的构建：

        当浏览器构建DOM树时，如果遇到复杂的DOM结构或者大量的DOM元素，会导致页面渲染被阻塞。

5、渲染树的构建：

        浏览器在构建渲染树时会合并DOM树和CSSOM树，生成最终的渲染树。如果CSSOM树的构建时间较长，会延迟页面的显示

6、字体加载：

        如果页面中使用了自定义字体或者远程字体，浏览器需要下载并解析这些字体文件，会阻塞页面的渲染。

7、图片加载：

        如果页面中有大量的图片需要加载，或者图片文件较大，会影响页面的加载速度。

8、重排和重绘：

        当页面中的元素样式发生改变时，浏览器会进行重排（reflow）和重绘（repaint），这也会影响页面的渲染速度。

四、【算法】相同的树

1、题目：

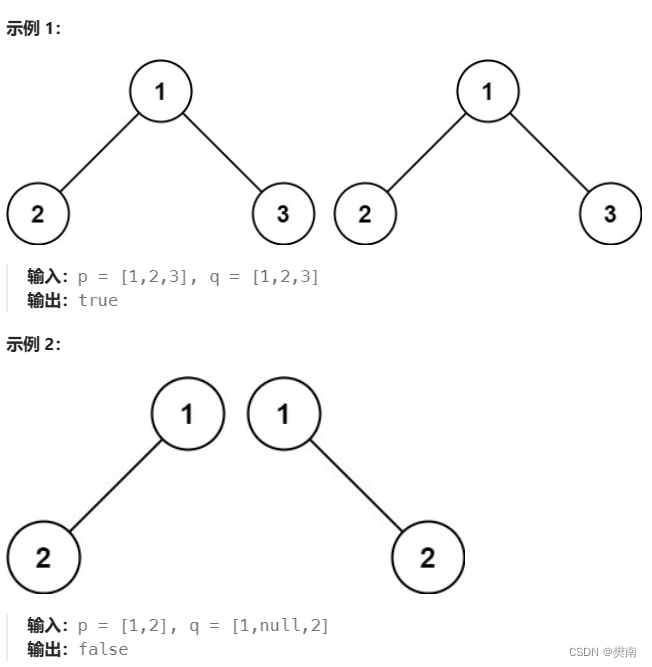
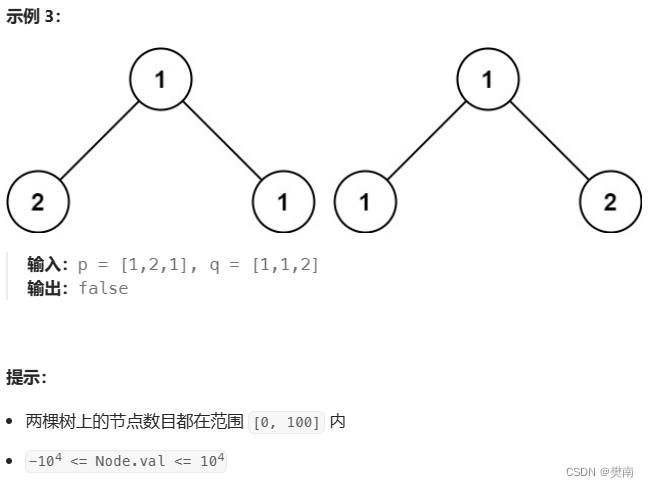
给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {}
2、解题：

这道题可以通过递归的方式来解决。具体的解题思路如下：

首先判断两棵树是否都为空，如果是，则认为它们相同，返回true。
然后判断其中一棵树为空的情况，如果有一棵树为空一棵树非空，则认为它们不同，返回false。
接着比较两棵树的根节点值是否相同，如果不同，则认为它们不同，返回false。
最后递归比较两棵树的左子树和右子树，如果左右子树都相同，则返回true，否则返回false。
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if (p == NULL && q == NULL) {return true; // 两棵树都为空，认为相同}if (p == NULL || q == NULL) {return false; // 一棵树为空，一棵树非空，认为不同}if (p->val != q->val) {return false; // 根节点值不同，认为不同}// 递归比较左右子树return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}