背景
在这篇文章中,我们将深入探讨GaussDB数据库中聚合函数的使用和优化。聚合函数是数据库查询中非常重要的工具,它们可以对一组值执行计算并返回单个值。例如,聚合函数可以用来计算平均值、总和、最大值和最小值。
这些功能在数据分析和报告中尤为关键。我们将通过实际示例展示如何有效地在GaussDB中应用这些聚合函数,同时也将探讨一些高级技巧,包括如何结合GROUP BY子句和使用窗口函数,以及如何优化查询性能。通过本文,您将获得关于GaussDB聚合函数的深入了解,为您的数据分析工作提供强大的支持。
一、聚合函数概述
聚合函数,顾名思义,就是会将数据记录聚合到一起的函数。
比如原先数据库中有100条记录,用聚合函数查询这100条记录中的最大值,最后输出的只有最大值的这一条记录。
聚合函数是SQL中用于在一系列值上执行计算并返回单一值的函数。在GaussDB中,常见的聚合函数包括:
SUM():计算数值列中所有值的总和。
AVG():计算数值列的平均值。
COUNT():统计一列中的元素数量,可以是所有元素或去重后的元素。
MAX()和MIN():分别找出一列中的最大值和最小值。
这些函数通常用于数据分析,特别是在处理大型数据集时,可以帮助快速得到关键数据指标。了解并有效使用这些聚合函数对于任何使用GaussDB进行数据处理的人来说都是必要的技能。
二、实际应用示例:
1、创建数据表和插入数据
销售数据表
CREATE TABLE sales (id INT,product VARCHAR(50),quantity INT,amount DECIMAL(10,2),sale_date DATE
);
插入数据:
INSERT INTO sales VALUES (1, '产品A', 10, 500.00, '2023-01-10');
INSERT INTO sales VALUES (2, '产品B', 5, 300.00, '2023-01-12');
INSERT INTO sales VALUES (3, '产品C', 15, 450.00, '2023-02-15');
产品类别表
CREATE TABLE products (id INT,name VARCHAR(50),category VARCHAR(50)
);
插入数据:
INSERT INTO products VALUES (1, '产品A', '电子');
INSERT INTO products VALUES (2, '产品B', '家具');
INSERT INTO products VALUES (3, '产品C', '电子');
员工工资表
CREATE TABLE employees (id INT,name VARCHAR(50),department VARCHAR(50),salary DECIMAL(10,2)
);
插入数据:
INSERT INTO employees VALUES (1, '张三', 'IT', 8000.00);
INSERT INTO employees VALUES (2, '李四', '财务', 9500.00);
INSERT INTO employees VALUES (3, '王五', 'IT', 7800.00);
总销售额统计
SELECT SUM(amount) FROM sales WHERE sale_date BETWEEN '2023-01-01' AND '2023-03-31';
产品类别统计
SELECT category, COUNT(*) FROM products GROUP BY category;
最高销售记录
SELECT MAX(quantity) FROM sales;
部门工资分析
SELECT department, AVG(salary) FROM employees GROUP BY department;
二、高级应用
1. 分组统计
分组聚合:
使用GROUP BY子句结合聚合函数,如SUM(),统计不同组别的数据总和。
SELECT department, SUM(salary) FROM employees GROUP BY department;
2. 窗口函数
使用窗口函数进行排序:
例如,使用ROW_NUMBER()为销售记录中每个产品的销售额进行排序。
SELECT product_name, sale_date, amount,ROW_NUMBER() OVER(PARTITION BY product_name ORDER BY amount DESC) AS rank
FROM sales;
三、GaussDB云原生数据库
GaussDB是一款高性能、高安全的云原生数据库,在数据库领域处于领先地位。作为一个高可靠性的全球化分布式关系型数据库,GaussDB数据库提供了丰富的存储过程支持,为存储过程的开发、管理和执行提供了更多的优化策略和高可用性保障。
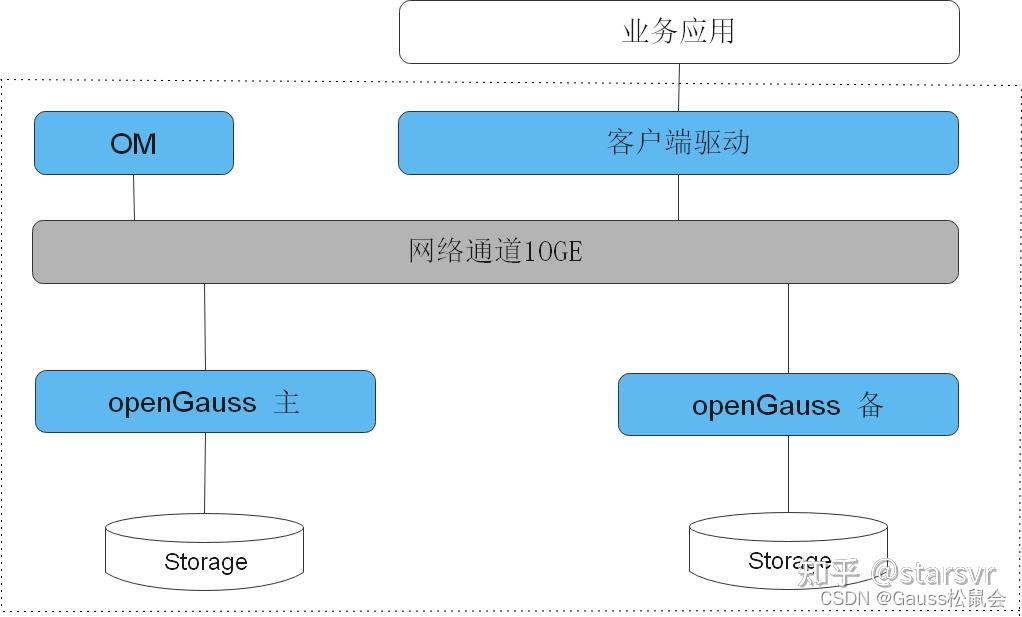
华为云GaussDB作为新一代分布式数据库,具备“五高两易”的核心技术竞争力,即高可用、高性能、高安全、高弹性、高智能、易部署、易迁移,充分满足金融客户对数据库的严苛要求。过去4年里,GaussDB经受了各国有大行数千亿行大表数据、数十万TPS/QPS、数亿存储过程的大数据量压测和极端场景考验,具有极其丰富的迁移经验,保证业务系统长期稳定运行。基于各大行业务对产品能力与迁移能力的充分验证,华为云GaussDB在城商农信银行、证券保险行业也完成了大规模的部署。
GaussDB是华为自主研发的企业级分布式关系型数据库,支持集中式和分布式两种部署方式。为企业提供了高可用,高可靠,高安全等能力,其产品全栈自研,并且具有完善生态工具和开源社区。在实际去O的项目过程,经常会遇到分区表的迁移,本文为大家介绍分区表设置自动新增分区。
华为云GaussDB还持续构建数据库生态。通过扩大伙伴生态圈,携手伙伴赋能行业人才;通过联合高校,进行产教融合,做厚人才基础。在行业应用上,GaussDB已全面覆盖金融到关键基础设施行业,保障客户业务安全。
四、总结
聚合函数在GaussDB数据库中的应用展示了其在数据处理和分析方面的强大能力。通过本文,我们不仅学习了基本聚合函数的使用,如SUM、AVG、COUNT、MAX和MIN,还探索了如何通过GROUP BY子句和窗口函数进行更复杂的数据分析。这些技能对于理解和分析大规模数据集至关重要。熟练掌握这些功能,可以显著提高在GaussDB中进行数据处理和分析的效率和准确性。
欢迎小伙伴们交流~
本文作者:hhh1218


时间片调度)

)

)

:通过下一代预测生成可扩展的图像)
)







)

)