博主总结:根据每个方案x各准则因素权重累加结果 对比来选择目标。数据主观性强
简介
AHP层次分析法是一种解决多目标复杂问题的定性和定量相结合进行计算决策权重的研究方法。该方法将定量分析与定性分析结合起来,用决策者的经验判断各衡量目标之间能否实现的标准之间的相对重要程度,并合理地给出每个决策方案的每个标准的权数,利用权数求出各方案的优劣次序,比较有效地应用于那些难以用定量方法解决的课题。
比如现在想选择一个最佳旅游景点,当前有三个选择标准(分别是景色,门票和交通),并且对应有三种选择方案。现通过旅游专家打分,希望结合三个选择标准,选出最佳方案(即最终决定去哪个景区旅游)。诸如此类问题即专家打分进行权重计算等,均可通过AHP层次分析法得到解决。
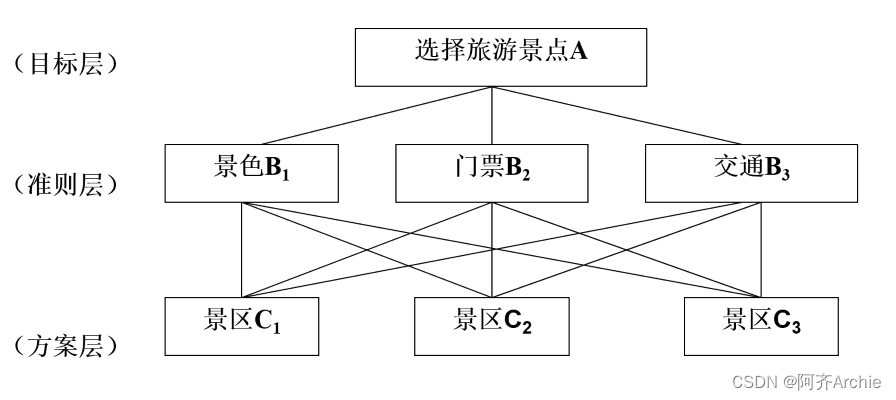
正如上述问题,专家可以对3个准则层标准(分别是景色,门票和交通)进行打分,得到3个选择标准对应的权重值;然后结合准则层得到的权重值,加上方案层的得分,最终选择出最佳方案。
- 特别提示
- 对于AHP层次分析法,即专家打分进行权重,专家打分需要遵循特殊的数据格式,即“判断矩阵”;
- AHP层次分析法包括两个步骤,分别是权重计算和一致性检验(SPSSAU会默认输出);
- SPSSAU需要手工输入判断矩阵数据即可完成分析,不需要上传。
分析结果表格示例如下:


AHP层次分析案例
1、背景
当前公司希望组织员工出去旅游,希望综合满足大家的要求,因此找到10位旅游专家,对旅游的4个影响因素(分别是景色,门票,交通和拥挤度)进行评价(即专家评价),最终得出四个影响因素的权重,然后结合权重值,对3个备选景点计算得分,选择出最佳旅游方案。
总共有4个评价因素(即准则层为4项,分别是景色,门票,交通和拥挤度),共有10位旅游专家进行打分,采用1-5分标度法,即比如A因素相对B因素非常重要,此时打5分,那么B因素相对于A因素就是1/5即0.2分。A因素相对B因素比较重要,此时打3分;A因素相对B因素重要程度一样,此时为1分。
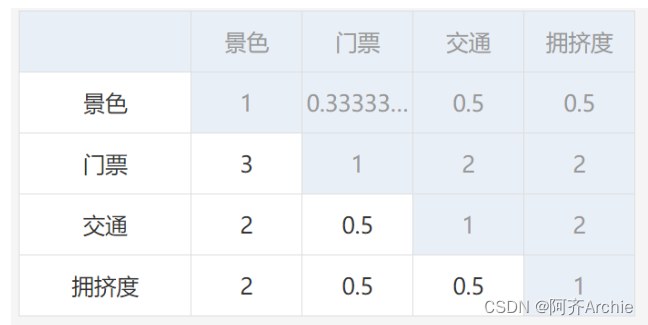
共有10个旅游专家打分,最终将10个旅游的打分进行计算平均分,得到最终的判断矩阵表格,如下表:

上表格显示:门票相对于景色来讲,重要性更高,所以为3分;相反,景色相对于门票来讲,则为0.33333分。交通相对于景色来更重要为2分,以及拥挤度相对于景色来讲更重要为2分。其余类似下去。
2、理论
完整的AHP层次分析法通常包括四个步骤,分别是:
- 第一步:标度确定和构造判断矩阵;
- 此步骤即为原始数据(判断矩阵)的来源,比如本例中使用1-5分标度法(最低为1分,最高为5分);并且结合出专家打分最终得到判断矩阵表格。
- 第二步:特征向量,特征根计算和权重计算;
- 此步骤目的在于计算出权重值,如果需要计算权重,则需要首先计算特征向量值,因此SPSSAU会提供特征向量指标。 同时得到最大特征根值(CI),用于下一步的一致性检验使用。
- 第三步:一致性检验分析;
- 在构建判断矩阵时,有可能会出现逻辑性错误,比如A比B重要,B比C重要,但却又出现C比A重要。因此需要使用一致性检验是否出现问题,一致性检验使用CR值进行分析,CR值小于0.1则说明通过一致性检验,反之则说明没有通过一致性检验。
针对CR的计算上,CR=CI/RI,CI值在求特征向量时已经得到,RI值则直接查表得出。
如果数据没有通过一致性检验,此时需要检查是否存在逻辑问题等,重新录入判断矩阵进行分析。 - 第四步:分析结论。
- 如果已经计算出权重,并且判断矩阵满足一致性检验,最终则可以下结论继续进一步分析。
1.判断矩阵为4阶判断矩阵

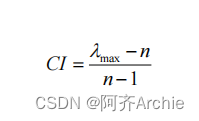

上表格输出包括特征向量这个中间计算过程值,同时输出权重值。最大特征根用于计算CI值;而CI值用于下面的一致性检验使用。
公司组织旅游,希望综合满足大家的要求,因此让10位旅游专家,对旅游的4个影响因素(分别是景色,门票,交通和拥挤度)进行评价(即专家评价),采用1-5分标度法,即比如A因素相对B因素非常重要,此时打5分;A因素相对B因素比较重要,此时打3分;A因素相对B因素重要程度一样,此时为1分。最终构建出判断矩阵,使用SPSSAU 18.0软件进行AHP层次分析。
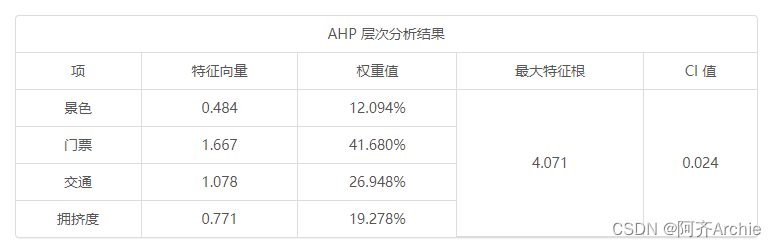
使用SPSSAU18.0软件进行分析,最终得出特征向量为(0.484,1.667,1.078,0.771),以及最大特征根值为4.071,CI值为0.024。最终总共4项(分别是景色,门票,交通和拥挤度)对应的权重值分别是:12.094%,41.680%,26.948%,19.278%。通过权重值大小可知,门票这个因素的权重最高为41.680%,其次为交通因素,权重为26.948%。

上表格为随机一致性RI表,本次研究判断矩阵为4阶,因此通过上表查看可以得出RI值为0.89。
本次研究构建出4阶判断矩阵,对应着上表可以查询得到随机一致性RI值为0.890,RI值用于下述一致性检验计算使用。

上表格展示一致性检验结果,CR=CI/RI,最终CR值为0.027,说明通过一致性检验。
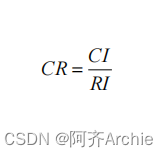
通常情况下CR值越小,则说明判断矩阵一致性越好,一般情况下CR值小于0.1,则判断矩阵满足一致性检验;如果CR值大于0.1,则说明不具有一致性,应该对判断矩阵进行适当调整之后再次进行分析。
本次针对4阶判断矩阵计算得到CI值为0.024,针对RI值查表为0.890,因此计算得到CR值为0.027 < 0.1,意味着本次研究判断矩阵满足一致性检验,计算所得权重具有一致性,即说明计算权重具有科学性。
![shell 脚本报错问题的解决归纳,如 [: missing `]‘](http://pic.xiahunao.cn/shell 脚本报错问题的解决归纳,如 [: missing `]‘)




复合类型、内存管理)









)



:SQL分类之DDL详解)