Day 23 669. 修剪二叉搜索树 108.将有序数组转换为二叉搜索树 538.把二叉搜索树转换为累加树总结篇

修剪二叉搜索树

给定一个二叉搜索树，同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树，使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点，所以结果应当返回修剪好的二叉搜索树的新的根节点。

669.修剪二叉搜索树

669.修剪二叉搜索树1

最直接的想法，遍历树然后找到root->val在[L,R]以外的节点删除，通过递归处理返回根节点；

如果此时简单的给出这种代码：

       root->left = trimBST(root->left, low, high);root->right = trimBST(root->right, low, high);

就会忽视掉当前节点不在范围内但是节点左(右)子树可能在范围内的情况；

如下图所示：

也就是在删除节点时，还要对其子树进行判断；至于实现方式可以参考上一题的子树嫁接方法，无须重构二叉树结构；

下面写递归三部曲：

首先确定递归函数参数和返回值：遍历整棵树，做修改，其实不需要返回值也可以完成修剪（其实就是从二叉树中移除节点）的操作；但是有返回值，更方便，可以通过递归函数的返回值来移除节点，不需要额外操作；

其次确定终止条件：修剪的操作并不是在终止条件进行的，所以就是遇到空节点返回就可以了；

最后确定单层递归的逻辑：嫁接子树，此处不再赘述；

递归代码如下：

	TreeNode* traversal(TreeNode* root, int L, int R){if(root == NULL)	return NULL;if(root->val < L){//节点值小于左边边界值TreeNode* tempNode = traversal(root->right, L, R);//此节点右子树中寻找所有大于L的值的节点，继续嵌套递归修剪右子树；return tempNode;}if(root->val > R)	return	traversal(root->left, L, R);//同理，并非直接return子树，而是修剪过后再returnroot->left = traversal(root->left, L, R);//对符合区间条件的根节点左右子树进行操作root->right = traversal(root->right, L, R);return root;}

将有序数组转换为二叉搜索树

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。

示例:

108.将有序数组转换为二叉搜索树

按题目要求切割数组得到平衡二叉搜索树，则从数组中间作为根节点开始切割；

同时注意循环不变量，因为这里是需要不断对数组进行切割直到子数组的长度为一；

遍历代码如下：

	TreeNode* traversal(vector<int>& nums, int L, int R){//确定函数参数和返回值//这里选择左闭右开的切割区间，则子区间停止切割的终止条件即是数组长度等于零的时候if(L >= R)	return NULL;//单层递归逻辑int mid = (R-L)/2+L;//防止int溢出TreeNode* root = new TreeNode(nums[mid]);//确定根节点root->left = traversal(nums, L, mid);//左闭右开root->right = traversal(nums, mid+1, R);return root;}

把二叉搜索树转化为累加树

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。节点的右子树仅包含键大于节点键的节点。左右子树也必须是二叉搜索树。

示例 1：

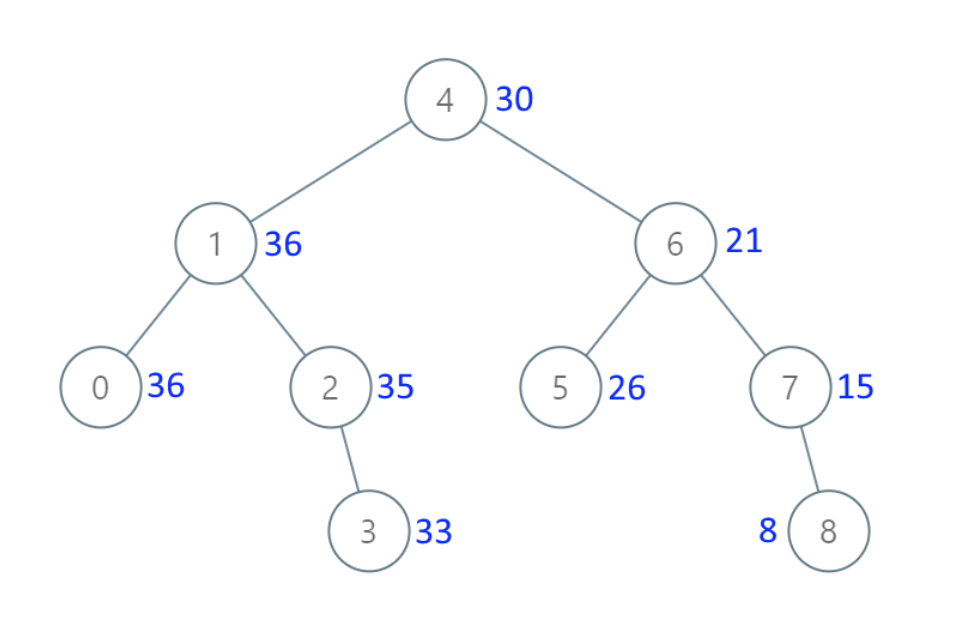
538.把二叉搜索树转换为累加树

输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

树中的节点数介于 0 和 104 之间。
每个节点的值介于 -104 和 104 之间。
树中的所有值互不相同 。
给定的树为二叉搜索树。

如果给定的是一个有序数组，则[1, 2, 3, 4]的结果就是[10, 9, 7, 4]，那二叉树呢？

从二叉搜索树的最大值开始往前递加，无疑就是处理顺序的改变，即右中左的顺序来遍历整个二叉搜索树，即反中序遍历；

则递归代码如下：

	int sum = 0;//记录前一个节点的数值void traversal(TreeNode* cur){//确定函数参数和返回值：遍历整棵树且无须对返回值进行处理if(!cur)	return;//确定终止条件：为空返回//if(cur->right)	sum += cur->right->val;	单层逻辑traversal(cur->right);cur->val += sum;sum = cur->val;//更新sum//if(cur->left)	sum += cur->left->val；traversal(cur->left);}

整体代码如下：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private:int sum = 0;//记录前一个节点的数值void traversal(TreeNode* cur){//确定函数参数和返回值：遍历整棵树且无须对返回值进行处理if(!cur)	return;//确定终止条件：为空返回//if(cur->right)	sum += cur->right->val;	单层逻辑traversal(cur->right);cur->val += sum;sum = cur->val;//更新sum//if(cur->left)	sum += cur->left->val；traversal(cur->left);}
public:TreeNode* convertBST(TreeNode* root) {sum = 0;traversal(root);return root;}
};