LUCF-Net: Lightweight U-shaped Cascade
Fusion Network for Medical Image Segmentation

摘要

在本研究中，通过添加Transformer，作者增强了现有U型神经网络架构在医学图像分割中的性能。尽管Transformer架构在提取全局信息方面非常强大，但由于其高复杂性，其在捕捉局部信息方面的能力有限。

为了应对这一挑战，作者提出了一种新的轻量级U型级联融合网络（LUCF-Net）用于医学图像分割。它采用了不对称的结构设计，并结合了局部和全局模块，以增强其在局部和全局建模方面的能力。

此外，还设计了一个多层级联融合解码网络，以进一步增强网络的信息融合能力。在CT格式的多器官数据集、MRI格式的心脏分割数据集以及图像格式的皮肤病学数据集上的验证结果表明，所提出的模型在处理局部-全局信息方面优于其他最先进的方法，在多器官分割上的Dice系数提高了1.54%，Hausdorff距离提高了2.6毫米。

此外，作为一个结合了卷积神经网络和Transformer架构的网络，它在使用仅有6.93百万个参数和6.6GB浮点运算的情况下，实现了具有竞争力的分割性能，无需预训练。总之，与其它基于Transformer的分割网络相比，所提出的方法在保持模型设计更简单的同时，展示了增强的性能。

Introduction

在医学图像分析领域，人工智能被认为是构建计算机辅助诊断应用的实际方法，尤其在图像分割方面。在这些基于人工智能的应用中，图像分割在促进疾病诊断和治疗策略制定方面起着关键作用。随着深度学习方法快速进步，卷积神经网络（CNN）和Transformer已成为近年来医学辅助分析研究的两个主要方向。这两种方法各有优势，为解决复杂的医学图像分割挑战提供了新的机遇。仅由带有上采样、下采样和跳跃连接的CNN组成的U-Net，在不同领域展示出了令人印象深刻的性能，同时保持了极小的复杂性。它在分割多个器官和皮肤病变等任务中表现出色，巩固了其在医学图像分割领域的独特地位。

然而，在医学图像分析中应用CNN仍存在挑战[5]。医学图像通常包含跨越大范围区域的丰富上下文信息，捕捉图像的整体结构、形状和分布。这种全面的视角对于精确诊断和治疗计划至关重要，要考虑到器官或组织内的整体布局、大小和空间关系等因素。利用这些远距离依赖，可以实现更准确和详细的医学图像分析。CNN在有效捕捉远距离相关性方面可能存在局限性，可能导致忽视全局信息，影响分割准确性。为了解决这个问题，利用自注意力机制Transformer模型受到了广泛关注。其出色的长距离依赖建模能力被引入到计算机视觉中，在图像分割任务中展示了显著成就。

与CNN相比，Transformer在某些医学图像领域方面具有优势。首先，Transformer可以捕获图像中像素间的全局依赖性，从而更好地理解整体结构。其次，Transformer可以提供更高的灵活性。传统的CNN模型通常需要手动设计网络结构，而Transformer模型可以通过简单的修改（如增加或减少层或头）来适应不同的任务。

因此，Transformer模型在处理各种视觉任务时更加灵活。尽管与CNN相比有这些优势，但Transformer有一个致命的缺陷[8]：基于Transformer的网络计算效率通常远低于CNN网络，导致计算成本高昂。因此，如何高效利用Transformer模型成为一个关键问题。

为了进一步提高医学图像分割的性能，研究行人开始探索结合CNN和Transformer的方法[9]。通过整合每种方法的优点，有可能改善医学图像中复杂属性和远距离依赖的处理，最终以降低模型复杂性的方式得到更准确和可靠的分割结果。然而，早期研究在结合CNN和Transformer时，只是简单地将它们合并在一起，而没有从根本上解决Transformer网络的复杂性问题。

在本研究中，受EdgeViTs的启发，提出了一种基于局部-全局特征级联的不对称CNN-Transformer网络。它在下采样后引入了 Patch 状自注意力，以实现局部和全局特征提取，同时显著降低了网络复杂性。通过在U形网络编码器中构建一个有效的局部-全局特征提取模块，使得由CNN提取的局部特征与由Transformer提取的全局特征有效整合。

本研究主要提供以下贡献：

通过将一个有效的局部-全局特征提取模块集成到U形网络编码器中，使源自CNN的局部特征与由Transformer提取的全局特征无缝整合。
设计了一种不对称的U形网络架构，以减少模型复杂性。在解码器中进行多层特征融合，并在训练过程中逐层计算损失，这加速了网络的收敛速度并增强了网络融合局部和全局信息的能力。
采用多种损失函数的新组合来解决数据集样本不平衡的问题，并通过在线硬样本学习策略进一步提高分割准确性。

Related Work

CNN-based Networks
早期医学图像分割方法大多采用纯卷积神经网络（CNN）结构。U-Net无疑是在这个领域的一个开创性工作。它结合了解码器、编码器和跳跃连接，为U形网络架构奠定了基础。在U-Net被提出之后，基于U-Net的各种方法也被引入。Diakogiannis等人使用了U-Net的编码器/解码器主干，并结合残差连接、孔洞模型、金字塔场景解析池和多任务推理来实现ResUNet-a模型，从而在保留U-Net的图像分割架构的同时，增强了特征传播和学习能力。通过实现一个注意力门控模块，Thomas等人能够利用特征图来捕捉全局信息，从而改进长距离依赖建模，增强了U-Net。

Do等人结合了全局方法和基于 Patch 的方法，利用多级距离特征实现全局信息建模。Guan等人融合了密集网络的概念，将每个解码器层的特征与之前的编码器层连接起来，以实现更鲁棒的特征传播。在改进版本如UNet++、IR-UNet++和UNet3+ 中，利用跳跃连接、多级特征融合和上采样结构，进一步增强了模型的信息传播和特征提取能力。在三维医学图像分割中，基于3D卷积的3D-UNet和VNet被引入，使得医学图像分割网络适用于体数据。上述基于CNN的方法主要采用多层特征融合、注意力机制等技术来弥补CNN网络在全局建模能力上的固有局限。因此，这些方法在一定程度上有助于性能的提升。

Transformer-based Networks
Transformer最初在自然语言处理（NLP）领域被引入，并以捕获广泛相互依赖性的卓越能力而闻名。Dsosovitskiy等人将Transformer的使用扩展到计算机视觉领域，通过将图像分割成 Token 以在Transformer网络中使用。这一突破极大地增强了网络提取全局特征的能力。作为一个开创性的尝试，TransUNet将Transformer集成到U形网络架构中。它不仅通过将图像特征编码为序列来编码强全局上下文，还通过U-Net混合网络设计充分利用低级CNN特征。Cao等人进一步结合了Swin Transformer，用Transformer网络替代了解码器和编码器，生成了一个纯Transformer U形网络来修复CNN网络在全局特征上的不足。

同样，DS TransUNet 采用密集网络构建了一个基于TransUNet基础的密集连接纯Transformer U形网络。面对Transformer固有的计算限制，越来越多的研究者开始研究更有效的基于Transformer的U-Net架构。Huang等人 提出了MISSFormer，它重新设计了编码器结构中的前馈网络，便于更高效地提取局部和全局上下文特征。Reza等人引入了DAEFormer，它重新定义了自注意力机制和跳跃连接路径。这种方法保证了在整个特征维度上包含空间和通道连接，保持了特征的可重用性，从而降低了自注意力机制的计算负担。大多数基于Transformer的U-Net架构要么结合CNN和Transformer，要么仅采用纯Transformer结构。

这些方法要么没有考虑到CNN在局部特征提取中的作用，要么使用CNN进行局部特征提取和Transformer进行全局特征提取，对来自CNN网络的特征执行自注意力操作，而没有解决Transformer自注意力机制的计算成本问题。尽管它们设法保持了某种程度的局部和全局特征建模，但往往伴随着高计算成本和模型参数。平衡网络性能和大小成为一项具有挑战性的任务。鉴于这些考虑，作者致力于构建一个高效的CNN-Transformer U形网络。

Proposed Method

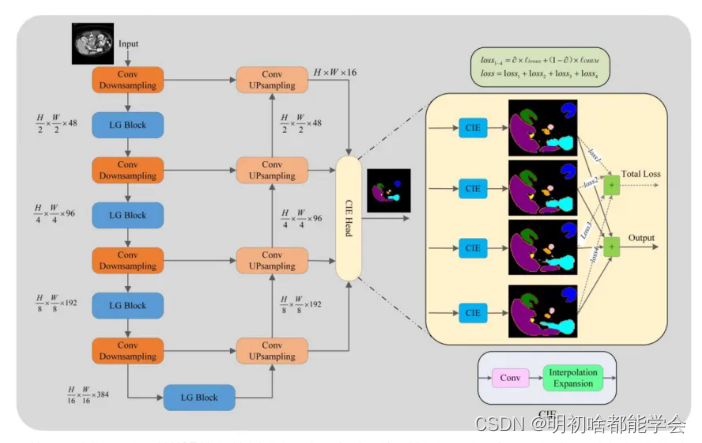
图1展示了LUCF-Net的完整结构，它采用了一个非对称的CNN-Transformer U形框架。核心组件是局部-全局特征提取模块（LG Block），它与编码器的下采样结构无缝集成。关于每个组件的详细信息将在后续章节中描述。

Local-Global Feature Extraction

在医学图像处理中，模型的全球建模能力在整体特征提取能力中扮演着关键角色。研究者们已经证实自注意力在处理图像的全局背景或长距离空间依赖性方面的重要影响[33]。然而，自注意力必须处理图像内部的大量空间冗余，例如在邻近区域中语义上相似的特征[34]。

因此，即使在降采样特征图上考虑所有标记也可能导致效率低下，浪费大量计算资源。为了在保留全局和局部上下文信息的同时减轻这一挑战，EdgeViTs提出了一种新颖的方法来处理这个问题。与在每一个空间位置执行自注意力的传统 Transformer 块不同，其自注意力模块仅针对一组标记子集计算自注意力。

尽管如此，它仍能实现类似于标准多头自注意力的全面空间交互。受到这种方法的启发，作者无缝地将稀疏自注意力集成到U形网络中。这种集成使作者能够在降低计算需求的同时，增强模型的局部-全局建模能力。

为了实现这一点，作者提出了一个名为LG Block的局部-全局特征提取模块，如图2所示。它接收传入的特征信息，并启动局部特征聚合操作，将信息汇聚到局部窗口中。随后，在通过均匀窗口采样获得的标记上执行注意力操作。最后，通过使用转置卷积的邻域扩散，传播来自注意力操作的全球上下文信息。该模块的公式描述如下：

Encoder and Decoder

在编码器部分，初始输入图像经过两个卷积层，随后进行下采样。在此过程之后，原始输入的分辨率减少了一半，而通道数相应增加。随后，下采样的图像被输入到LG块中，在那里执行自注意力操作。这个序列在四层卷积下采样和四个LG块中重复。解码层仅使用卷积和上采样操作。

同样，对于每一层卷积和上采样，图像分辨率都会翻倍。这个过程通过四层上采样层重复，产生与原始输入相匹配的图像尺寸。需要强调的是，解码器部分不使用LG块，通过使用跳跃连接和多层级联模块，可以在编码器中融合局部和全局层次的信息，从而避免了在解码器中使用Transformer，并减少了模型大小。

Feature Fusion

传统的U-Net网络通常使用解码侧的最后一层作为综合网络输出，并在训练过程中计算损失。为了在多尺度图像输出情况下提高分割效果，通过跳跃连接将来自不同编码器层的多尺度信息整合到解码器中，以增强架构。解码器中每层的上采样输出都输入到独立的解耦头中。这个解耦头对应于图1中的CIE头，它将不同尺度的图像协调成一致的输出大小。

CIE头使用双线性插值操作，这与解码器上的上采样操作相同。在训练过程中，作者通过比较每层的输出及其相应的标签来计算损失。最终输出是四个不同阶段的输出的总和。这种结构通过多级级联加强像素间的空间关系，加速训练期间模型的收敛。

Loss Function

在医学图像分割中，交叉熵损失和Dice损失是最常用的损失函数[25]。Dice系数是在视觉计算领域中广泛使用的一个度量标准，用于测量两张图像之间的相似性。然而，Dice损失在训练过程中表现出显著波动，因此，它经常与交叉熵损失函数结合使用。

在这里，作者引入了Lovasz Softmax损失[35]来替代Dice损失。作者做出这一选择是因为这个损失也直接优化基于区域的指标。它是一个凸函数，确保在训练过程中不会陷入局部最小值。此外，Lovasz Softmax损失在处理目标边界像素方面表现良好，避免了模糊边缘的产生。Lovasz Softmax损失源自Jaccard指数损失的一个变体，其类别可以表示为以下公式：

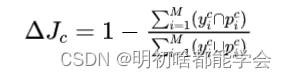
在这里，$g_i$ 和 $p_i$ 分别表示第 $i$ 个像素的标签和网络预测，$c$ 是类别，$M$ 是批次中的像素数。公式 (5) 是一个离散函数，不适合直接优化损失。Lovasz 扩展被用于使 Jaccard 指数损失可微，从而将离散输入值转换为连续值。在这里，KaTeX parse error: Expected group after '^' at position 6: f_i(p^̲%) 是网络在类别 $c$ 上的输出概率分布，由 Softmax 函数得到。$e_i(c)$ 是类别 $c$ 的像素误差，向量 $e(c)$ 是类别 $c$ 的 Jaccard 指数的替代。$△J$ 是 Jaccard 指数的 Lovasz 扩展。
为了减轻数据集中的样本不平衡问题，引入了在线困难样本挖掘（OHEM）损失函数[36]。在深度学习模型的训练中，这种损失函数策略用于解决由类别分布不平衡引起的问题。OHEM损失的目的在于关注难以分类的样本，鼓励模型更好地学习困难情况，从而提高整体性能。

在训练阶段，OHEM损失的核心思想是从批量中选择难以分类的样本进行反向传播。这有效地引导模型关注具有挑战性的实例，帮助模型更好地区分不同类别。自然地，作者将OHEM损失函数中困难样本的定义扩展到像素 Level 。对于每组训练批量，初始损失函数计算当前批次中所有像素训练的平均交叉熵损失。

基于交叉熵损失，OHEM损失公式可以表述为：

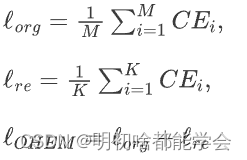
在这里，$L_{org}$ 和 $l_i$ 分别代表所有像素的损失和与所选困难像素相关的损失。变量 $K$ 表示困难像素的数量，这些像素是通过过滤掉置信度低的预测像素来确定。OHEM损失选择了这些置信度低的像素并计算它们的平均交叉熵损失。随后，困难像素的平均损失与所有像素的平均交叉熵损失进行聚合。

总之，作者的混合损失可以按如下方式确定：
$$[\text{loss}=0\times l_{house}+(1-c)\times l_{OHEM}]$$