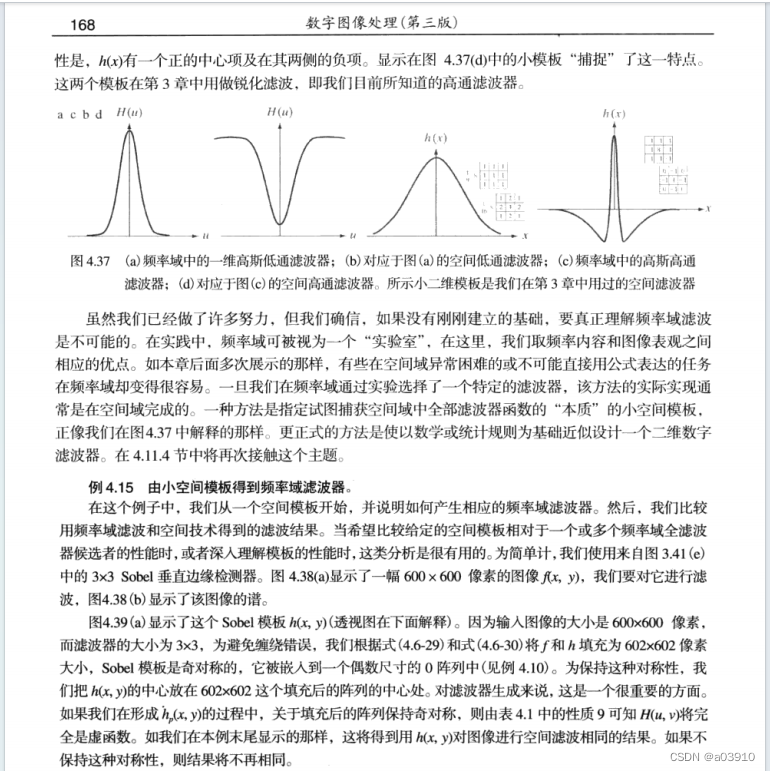
说实话，4.7.4的前面的图4.37我没看懂在说什么，但是例4.15这个我倒是看明白了。中心思想是:本来空间滤波器计算的时候需要不停地滑动模版的，这里把滑动用x的值代替了,但是现在不搞滑动了，利用傅里叶变换和卷积公式，只要计算出来公式4.7-1的关于(x,y)的函数值，就是相当于让位置(x,y)走遍了图像上所有的位置。而原本的滑动本来也只是计算(x,y)的函数值，原来的空间域的卷积确实函数不需要尺寸一致，而换成频率域相乘之后，必须要尺寸一致，原因解释过了，实际上原来的空间域的函数就算是补充零，不用傅里叶变换直接进行空间卷积运算还是不影响结果的。

但是还是有问题，为什么图像和模版均需要中心化？

sobel模版这是微分算子的模版吧，转化为频率域的滤波器的时候。总是中心化，因为4.7.3小节的步骤总结也是把图像中心化了。图像为什么中心化？假设原图是[0,256]x[0,256]，到频率域上就是[0,256]x[0,256]。但实际上频率域是周期函数，所以图像中心化意味着在（0,0）位置的直流分量移动到了[0,256]x[0,256]的中心位置，其实只是周期函数平移而已。模版在频率域也要平移，因为这样，在空间卷积计算的时候是fh=F-1{[(F(f*(-1)^(x+y)))*F((h*(-1)^(x+y)))]*(-1)^(x+y)}。感觉有道理，但是我无法简单的从数学计算得到不管这个了。我还是没有解释为什么图像中心化，我只能猜测书上说过模版中心化可以简化模版的技术要求，在4.7.2小节的开始的一顿描述中，所以是因为模版要中心化，所以图像要配合？

接下来考虑点列的中心问题。以一维为例，3个点的中心必然是第1个点（从第0个算起），4个点的中心是第2个点（从第0个算起），为什么会这样呢？我不知道，但是例4.15的中心化的过程就是这样的。

还有最后一个问题，图4.39的b和d的图是一样的，但是缠绕误差呢？

这里的模版很小，图像很大，仿造这种情况做一个一维的例子: f(x)=x, M=15, h(x)=1, N=2.

所以P=M+N-1=16。

1 2 3 4 5 6 7 8 9 10 12 13 14 15 0 1 2 3 4 5 6 7 8 9 10 12 13 14 15

                                        0....0 0 1 1 0 0....0 0

这里并没有缠绕误差，因为缠绕误差是频率域中的滤波器直接使用的时候（如果频率域滤波器转化为空间域滤波器不是零填充会产生）发生的。这里是直接从空间模版填充零，转频率域滤波器了，所以并没有什么问题。

所以问题的关键是如何生成频率域滤波器。直接给出频率域滤波器是有缠绕误差这个问题的。但是如果已知频率域滤波器的连续函数，和图像，图像本身是离散函数。频率域滤波器的连续函数转化为空间域滤波器的连续函数，接下来是有限次取样的问题了，该取多少个，以及位置，以及需要和图像填充多少个零配合，使得在滑动模版的运算中（模版的滑动其实两个周期循环移动的）最接近（模版在填充零之后的循环移动的计算过程），但是这种取样之后得到的离散函数的傅里叶变换和原来的连续频率域滤波器还是有区别的，在（u0,v0）上原来的值和现在的值不一样。差多少我也不知道。