目录
简述
理解梯度
什么是梯度
计算梯度
政安晨的个人主页:政安晨
欢迎 👍点赞✍评论⭐收藏
收录专栏: 政安晨的机器学习笔记
希望政安晨的博客能够对您有所裨益,如有不足之处,欢迎在评论区提出指正!
简述
在深度学习神经网络中,反向传播是一种用来训练神经网络的常用方法。它通过计算损失函数对于网络参数的梯度,然后使用梯度下降算法更新参数,以降低损失函数的值。
梯度表示了函数在某一点上的变化率和方向,对于神经网络而言,梯度表示了损失函数对于网络参数的变化率和方向。在反向传播过程中,首先通过前向传播计算出网络的输出和损失函数的值,然后利用链式法则逐层计算参数的梯度。
具体来说,反向传播的过程可以分为两个步骤:反向传播和参数更新。
在反向传播过程中,从输出层开始,通过链式法则计算每一层的梯度。首先计算输出层的梯度,然后反向传播到上一层,重复这个过程直到输入层。
在参数更新过程中,根据梯度的方向和大小,使用梯度下降算法来更新参数。梯度下降算法根据梯度的反方向调整参数的值,以使损失函数的值逐渐降低。具体来说,参数的更新公式可以表示为:参数 = 参数 - 学习率 * 梯度。
在深度学习中,梯度的理解非常重要。梯度可以告诉我们当前参数的变化趋势,通过不断迭代调整参数,使得损失函数逐渐减小,从而提高神经网络的性能。
反向传播是训练神经网络的最常用方法之一。Rumelhart、Hinton和Williams(1986)引入了反向传播,该方法到今天仍然很流行。程序员经常使用反向传播训练深层神经网络,因为在图形处理单元上运行时,它的伸缩性很好。
要了解这种用于神经网络的算法,我们必须探讨如何训练它,以及它如何处理模式。经典的反向传播已得到扩展和修改,产生了许多不同的训练算法。
理解梯度
反向传播是梯度下降的一种,许多教科书中通常互换使用这两个术语。梯度下降是指针对每个训练元素,在神经网络中的每个权重上计算一个梯度。由于神经网络不会输出训练元素的期望值,因此每个权重的梯度将为你提示如何修改权重以实现期望输出。如果神经网络确实输出了预期的结果,则每个权重的梯度将为0,这表明无需修改权重。
梯度是权重当前值下误差函数的导数。误差函数用于测量神经网络输出与预期输出的差距。实际上,我们可以使用梯度下降,在该过程中,每个权重的梯度可以让误差函数达到更低值。
梯度实质上是误差函数对神经网络中每个权重的偏导数。每个权重都有一个梯度,即误差函数的斜率。权重是两个神经元之间的连接。计算误差函数的梯度可以确定训练算法应增加,还是减小权重。反过来,这种确定将减小神经网络的误差。误差是神经网络的预期输出和实际输出之间的差异。许多不同的名为“传播训练算法”的训练算法都利用了梯度。
总的来说,梯度告诉神经网络以下信息:
● 零梯度——权重不会导致神经网络的误差;
● 负梯度——应该增加权重以减小误差;
● 正梯度——应当减小权重以减小误差。
由于许多算法都依赖于梯度计算,因此我们从分析这个过程开始。
什么是梯度
首先,让我们探讨一下梯度。本质上,训练是对权重集的搜索,这将使神经网络对于训练集具有最小的误差。如果我们拥有无限的计算资源,那么只需尝试各种可能的权重组合,来确定在训练期间提供最小误差的权重。
因为我们没有无限的计算资源,所以必须使用某种快捷方式,以避免需要检查每种可能的权重组合。这些训练算法利用了巧妙的技术,从而避免对所有权重进行蛮力搜索。但这种类型的穷举搜索将是不可能的,因为即使小型网络也具有无限数量的权重组合。
请考虑一幅图像,它展示每个可能权重的神经网络误差。
下图展示了单个权重的误差。

从上图可以看出:最佳权重是曲线的值最低的位置。问题是我们只看到当前权重的误差;我们看不到整幅图像,因为该过程需要穷尽的搜索。但是,我们可以确定特定权重下误差曲线的斜率。在这个例子中,斜率或梯度为−0.562 2。负斜率表示增大权重会降低误差。
梯度是指在特定权重下误差函数的瞬时斜率。
误差曲线在该点的导数给出了梯度。这条线的倾斜程度告诉我们特定权重下误差函数的陡峭程度。导数是微积分中最基本的概念之一。
对于本文,你只需要了解导数在特定点处提供函数的斜率即可。训练技巧和该斜率可以为你提供信息,用于调整权重,从而降低误差。现在,利用梯度的实用定义,我们将展示如何计算它。
计算梯度
我们将为每个权重单独计算一个梯度。我们不仅关注方程,也关注梯度在具有真实数值的实际神经网络中的应用。下图展示了我们将使用的神经网络——XOR神经网络。
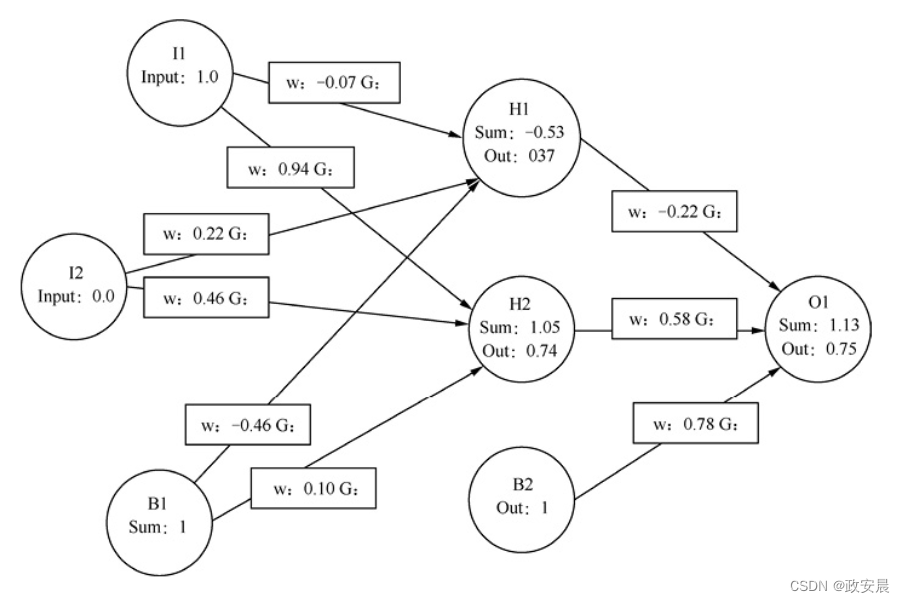
此外,在本文中,我们将展示一些计算,说明神经网络的训练。
我们必须使用相同的起始权重,让这些计算保持一致。但是,上述权重没有什么特征,是由该程序随机生成的。前面提到的神经网络是典型的三层前馈神经网络,就像我们之前研究的那样,圆圈表示神经元,连接圆圈的线表示权重,连接线中间的矩形给出每个连接的权重。
我们现在面临的问题是,计算神经网络中每个权重的偏导数。当一个方程具有多个变量时,我们使用偏导数。每个权重均被视为变量,因为这些权重将随着神经网络的变化而独立变化。每个权重的偏导数仅显示每个权重对误差函数的独立影响。该偏导数就是梯度。
可以用微积分的链式规则来计算每个偏导数。我们从一个训练集元素开始。对于上图,我们提供[1,0]作为输入,并期望输出是1。你可以看到我们将输入应用于上图。第一个输入神经元的输入为1.0,第二个输入神经元的输入为0.0。
该输入通过神经网络馈送,并最终产生输出。第4章“前馈神经网络”介绍了计算输出与总和的确切过程。反向传播既有前向,也有反向。
计算神经网络的输出时,就会发生前向传播。我们仅针对训练集中的这个数据项计算梯度,训练集中的其他数据项将具有不同的梯度。在后文,我们将讨论如何结合各个训练集元素的梯度。现在我们准备计算梯度。
下面总结了计算每个权重的梯度的步骤:
● 根据训练集的理想值计算误差;
● 计算输出节点(神经元)的增量;
● 计算内部神经元节点的增量;
● 计算单个梯度。
:springboot内嵌tomcat)


)















