解法：直接给算法
创建一个栈和一个空的后缀表达式字符串。
遍历中缀表达式中的每个字符。
如果当前字符是操作数，直接将其添加到后缀表达式字符串中。
如果当前字符是操作符，需要将其与栈顶的操作符进行比较：
如果栈为空，或者栈顶操作符是左括号'('，则将当前操作符压入栈中。
如果当前操作符的优先级大于栈顶操作符的优先级，将当前操作符压入栈中。
如果当前操作符的优先级小于等于栈顶操作符的优先级，将栈顶操作符弹出并添加到后缀表达式字符串中，然后继续比较当前操作符与新的栈顶操作符，直到符合压入条件。
如果当前字符是'('，将其压入栈中。
如果当前字符是')'，需要将栈中的操作符弹出并添加到后缀表达式字符串中，直到遇到左括号为止。将左括号弹出，但不添加到后缀表达式字符串中。
遍历完所有字符后，将栈中剩余的操作符弹出并添加到后缀表达式字符串中。
返回后缀表达式字符串。
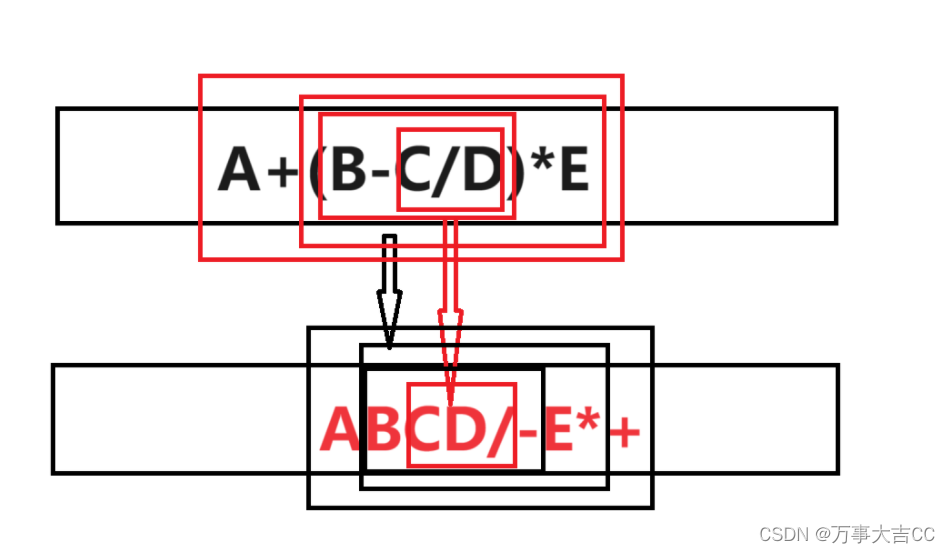
原则就是：有括号先算括号里的，先乘除（优先级2），再加减（优先级1）
#include<iostream>
#include<string>
#include<stack>
using namespace std;bool isop(char c) {if (c == '+' || c == '-' || c == '*' || c == '/') {return true;}else return false;
}
int jibie(char op) {if (op == '+' || op == '-') {return 1;}else if (op == '*' || op == '/') {return 2;}return 0;
}
string trans(string s) {string p;stack<char> sk;for (int i = 0; i < s.size(); i++) {char c = s[i];if (c >= 'a' && c <= 'z' || c >= 'A' && c <= 'Z' || c >= '0' && c <= '9') {p += c;}else if (isop(c)) {while (!sk.empty() && jibie(sk.top()) >= jibie(c)) {p += sk.top();sk.pop();}sk.push(c);}else if (c=='(') {sk.push(c);}else if (c == ')') {while (!sk.empty() && sk.top() != '(') {p += sk.top();sk.pop();}sk.pop();}}while (!sk.empty()) {p += sk.top();sk.pop();}return p;
}
int main() {string str;cin >> str;cout << trans(str);return 0;
}
