【为什么 Softmax 函数面对二分类问题时可以简化为 Sigmoid 函数】
将二分类问题当成普通多分类问题,神经网络如下所示:
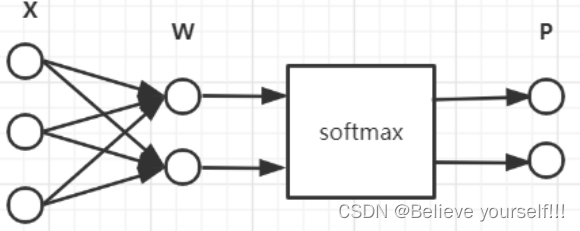
因为有两个分类,所以需要有两个输出,然后经过 Softmax 后得到每个分类的预测概率。
假设第一个分类的得分为,第二个分类得分
,则经过
Softmax 层后得到 第一个分类的概率为:
第二个分类的概率为:
令 ,所以
和
可以重写为:
此时将和
相加可以非常惊奇的发现:
,也就是说我们只需要计算出来一个P,然后另一个直接通过1-P即可计算出来。
这两个概率随得分
的变化图像如下所示:
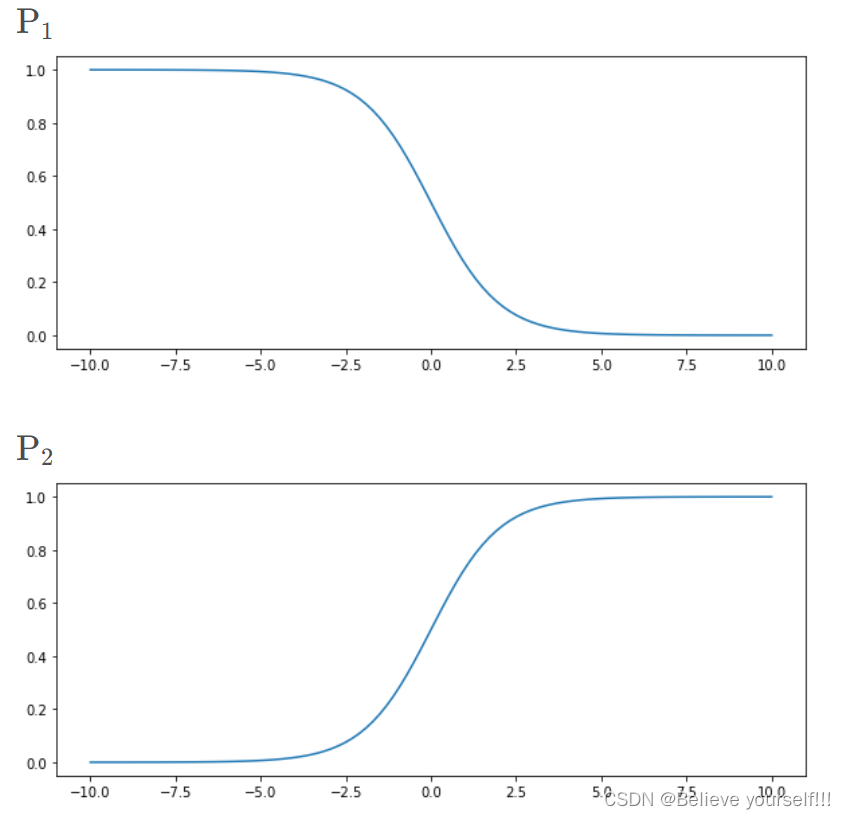
由上图可见,采取 的公式时,
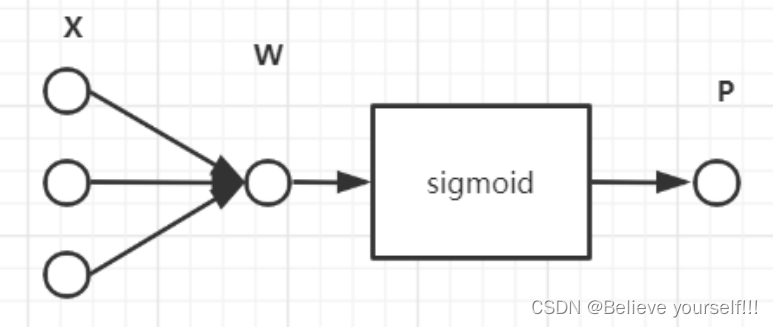
越大,P的取值越接近1,符合我们的直觉,所以选择这个作为Sigmoid函数。于是上述神经网络可以简化为只有一个输出的神经网络,然后经过Sigmoid函数得到预测为分类1的概率P,另一个分类的概率为1-P,新神经网络只需要训练一个权重W和偏移量b即可。
【二分类情况下 softmax 和 Sigmoid 函数的区别】
说到softmax和sigmoid二者差别,就得说说二者分别都是什么。其实很简单,网上有数以千计的优质博文去给你讲明白,我只想用我的理解来简单阐述一下:
- sigmoid函数针对两点分布提出。神经网络的输出经过它的转换,可以将数值压缩到(0,1)之间,得到的结果可以理解成“分类成目标类别的概率P”。而不分类到该类别的概率,就是(1 - P),这也是典型的两点分布的形式;
- softmax本身针对多项分布提出,当类别数是2时,它退化为二项分布,而它和sigmoid真正的区别就在这儿——二项分布包含两个分类类别(姑且分别称为A和B);而两点分布其实是针对一个类别的概率分布,其对应的那个类别的分布,直接由1-P粗暴得出。
据上所述,sigmoid函数,我们可以当作成它是对一个类别的“建模”。将该类别建模完成,另一个相对的类别就直接通过1减去得到;
而softmax函数,是对两个类别建模。同样的,得到两个类别的概率之和也是1.
神经网络在做二分类时,使用softmax还是sigmoid,做法其实有明显差别。由于softmax是对两个类别(正反两类,通常定义为0/1的label)建模,所以对于NLP模型而言(比如泛BERT模型),Bert输出层需要通过一个nn.Linear()全连接层压缩至2维,然后接softmax(pytorch的做法,就是直接接上torch.nn.CrossEntropyLoss);而sigmoid只对一个类别建模(通常就是正确的那个类别),所以Bert输出层需要通过一个nn.Linear()全连接层压缩至1维,然后接sigmoid(torch就是接torch.nn.BCEWithLogitsLoss)
总而言之,sotfmax和sigmoid确实在二分类的情况下可以化为相同的数学表达形式,但并不意味着二者有一样的含义,而且二者的输入输出都是不同的。sigmoid得到的结果是“分到正确类别的概率和未分到正确类别的概率”,softmax得到的是“分到正确类别的概率和分到错误类别的概率”。
一种常见的错法,即,错误地将softmax和sigmoid混为一谈,在把BERT输出 层压缩至2维的情况下,却用sigmoid对结果进行计算。这样我们得到的结果其意义是什么呢?
假设我们现在BERT输出层经nn.Linear()压缩后,得到一个二维的向量:
[-0.9419267177581787, 1.944047451019287]
对应类别分别是(0,1)。我们经过sigmoid运算得到:
tensor([0.2805, 0.8748])
前者0.2805指的是分类类别为0的概率,0.8748指的是分类类别为1的概率。二者相互独立,可看作两次独立的实验(显然在这里不适用,因为0-1类别之间显然不是相互独立的两次伯努利事件)。所以显而易见的,二者加和并不等于1.
若用softmax进行计算,可得:
tensor([0.0529, 0.9471])
这里两者加和是1,才是正确的选择。
参考:
为什么 softmax 函数面对二分类问题时可以简化为 sigmoid 函数_将softmax结果转换为sigmoid值-CSDN博客
https://www.cnblogs.com/wynlfd/p/14101373.html







)



---公共钥匙盒(线性表,栈,队列))

流量控制)

nacosgateway(2)gatewayspringsercurity)
 可编程性)


