一、满足条件的值

1. 审题

已知：$S=1+2+4+7+11+16\dots$
递归求解刚好大于等于 $5000$ 时 $S$ 的值。

2. 参考答案

#include <iostream>
using namespace std;// 定义递归函数，计算第x个数的值
int f(int x)
{int r;if (x == 1) r = 1; // 第一个数为 1else r = f(x-1) + x-1; // 第 x 个数为第 x-1 个数加上 x-1return r;
}int main()
{int s = 0, i = 1; // 初始化累加和 s 为 0，计数器 i 为 1while (s <= 5000) // 循环累加直到 s 大于 5000{s += f(i++); // 将第 i 个数的值累加到 s 上，并将 i 自增}cout << s; // 输出累加和return 0;
}

二、递归组合数

1. 审题

从 $n$ 个物品里面选出 $m$ 个物品的方案数，记为 $C(n,m)$。对于递归过程如下理解：假设 $n$ 个物品里面有一个物品最特殊，挑选时 $m$ 个物品时，这个特殊物品假定不需要挑选出来，此时要从 $n$ 个物品里选出 $m$ 个物品，就相当于要从 $n-1$ 个物品里面挑选出 $m$ 个物品记为：$C(n-1,m)$ 。如果挑选出来物品中有这个特殊的物品，则挑选的方式就是从 $n-1$ 个物品中挑选出 $m-1$ 个物品记为：$C(n-1,m-1)$。所以 $C(n,m)=C(n-1,m)+C(n-1,m-1)$。特别的当 $n$ 和 $m$ 相等时或者挑选的数是 $0$ 时，方案数规定为只有 $1$ 种，表述为$C(n,n)=C(n,0)=1$。现在请你从电脑中输入两个正整数，分别表示 $n$ 和 $m$，求从 $n$ 个物品中选择 $m$ 个物品，总共有多少选择方法？

2. 参考答案

#include <iostream>
using namespace std;// 递归计算组合数
int c(int n, int m)
{// 完全按照题目说的来if (n == m || m == 0) return 1;return c(n-1, m) + c(n-1, m-1);
}int main()
{int n, m;cin >> n >> m;cout << c(n, m);
}

三、你的变换

1. 审题

你有一个数 $a$，你想把这个数变成 $b$，为此你可以做两种变换：
① 把现有的数 $x$ 变为 $2x$;
② 把现有的数 $x$ 后面接一个 $1$（即 $x$ 变为 $10x+1$）
例如：2 -> 4 -> 8 -> 81 -> 162
你需要帮可多判断一下，把 $a$ 变成 $b$ 的可能性。

2. 参考答案

#include <iostream>
using namespace std;// 递归判断是否存在变换路径
bool transform(int a, int b)
{if (a == b) return 1; // 当 a 和 b 相等时，变换成功，返回 trueif (a > b) return 0; // 当 a 大于 b 时，无法变换，返回 falsereturn transform(a*2, b) || transform(a*10+1, b); // 递归进行两种变换判断
}int main()
{int a, b;cin >> a >> b;cout << (transform(a, b) ? "YES" : "NO"); // 输出是否存在变换路径return 0;
}

四、递归方块

1. 审题

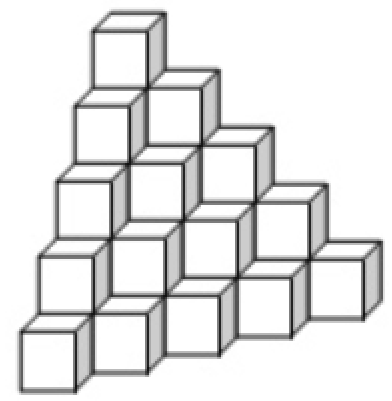
给出层数，求方块总数。

2. 参考答案

#include <iostream>
using namespace std;int n;
int sum;int f(int x)
{if (x == 1) return 1;return f(x-1) + x;
}int main()
{cin >> n;while (n){sum += f(n--);}cout << sum;return 0;
}

五、达到回文的次数

1. 审题

回文数的定义为：如果把一个数的各个数位上的数字颠倒过来得到的新数与原数相等，则此数是回文数。$7,22,131,2112,31013,\dots$ 都是回文数。对任意给出的一个整数 $n$，经过一系列的处理，最后都能成为回文数。处理的方法是，该数加上它的颠倒数。
例如：
$n=176$；
第一次处理后 $176+671＝847$；
第二次处理后 $847+748＝1595$；
第三次处理后 $1595+5951＝7546$；
第四次处理后 $7546+6457＝14003$；
第五次处理后 $14003+30041＝44044$；
此时成为回文数，共进行 $5$ 次处理。
问题：给出 $n$ 后，求出使该数按照以上规则进行一系列处理后成为回文数的最少操作次数。

2. 参考答案

#include <iostream>
#include <string>
#include <algorithm>
using namespace std;string n;
int cnt;// 将字符串 n 翻转
string reverse(string n)
{reverse(n.begin(), n.end());return n;
}// 递归函数
void palin(string n)
{string reversed = reverse(n);long long n2 = stoll(n); // string -> long longlong long rev = stoll(reversed); // string -> long longlong long sum = n2 + rev; // 本身 + 颠倒cnt++; // 次数增加if (to_string(sum) == reverse(to_string(sum))) return; // 已经回文return palin(to_string(sum)); // 没有回文，继续递归
}int main()
{cin >> n;if (n != reverse(n)){palin(n);}else{cout << 0;return 0;}cout << cnt;return 0;
}