目录
前言
提供
软件
系统展示
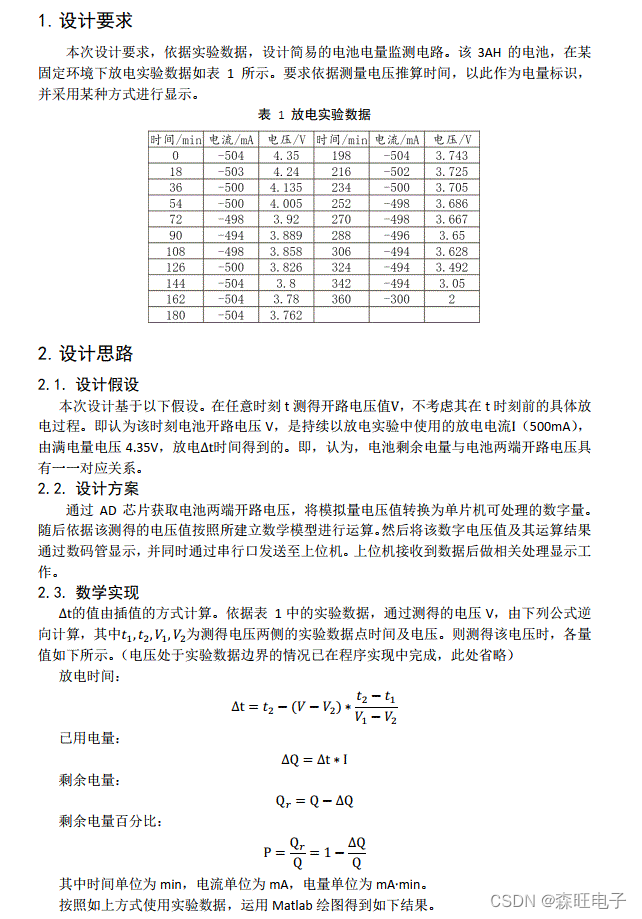
1.放电试验及其处理
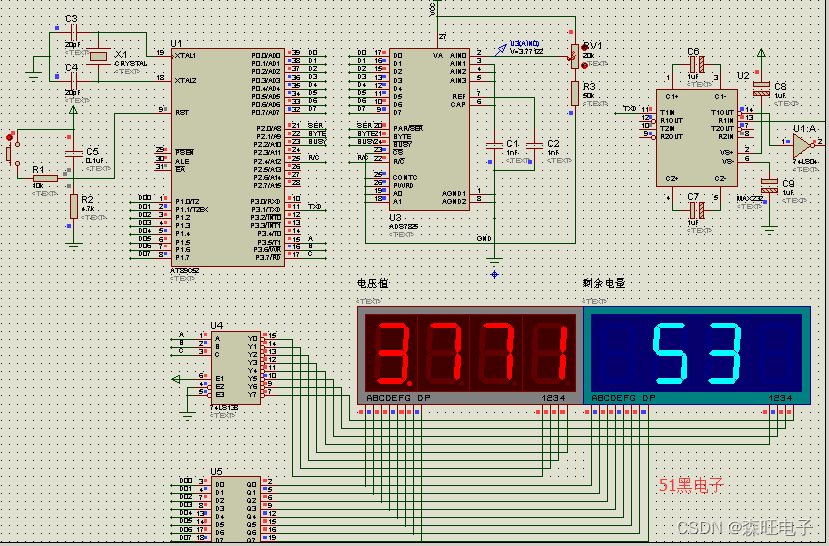
2.硬件系统原理图
3.下位机程序
4.显示
5.上位机界面
6.上位机程序
7.文档
资料下载地址:电池电量监测系统设计 单片机+LabVIEW+Matlab+Protues+Keil程序
前言
这套系统首先使用Matlab分析获得了电压-电量之间的关系曲线。随后在单片机上存储了该曲线的信息,通过插值方式求取通过AD得到的电压对应的剩余电量。系统通过Protues进行了仿真。并将数据结果通过串口传送至了由Labview编写的上位机。
提供
本贴提供的文件包括:1.Keil编写的程序(C)
2.Protues仿真文件
3.Matlab分析绘图程序
4.Labview编写的上位机程序
5.作业报告
软件
如果需要完整的运行本贴提供的全部内容,需要安装以下软件。
1.Keil 2.Protues 3.Labview 4.Matlab 5.虚拟串口
系统展示
1.放电试验及其处理
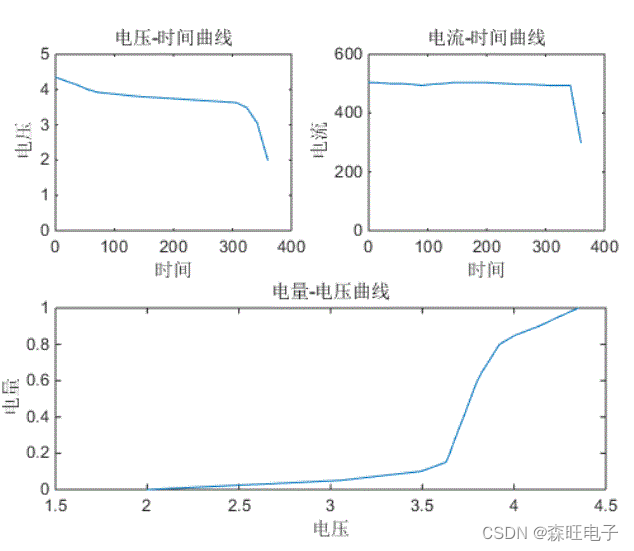
2.硬件系统原理图
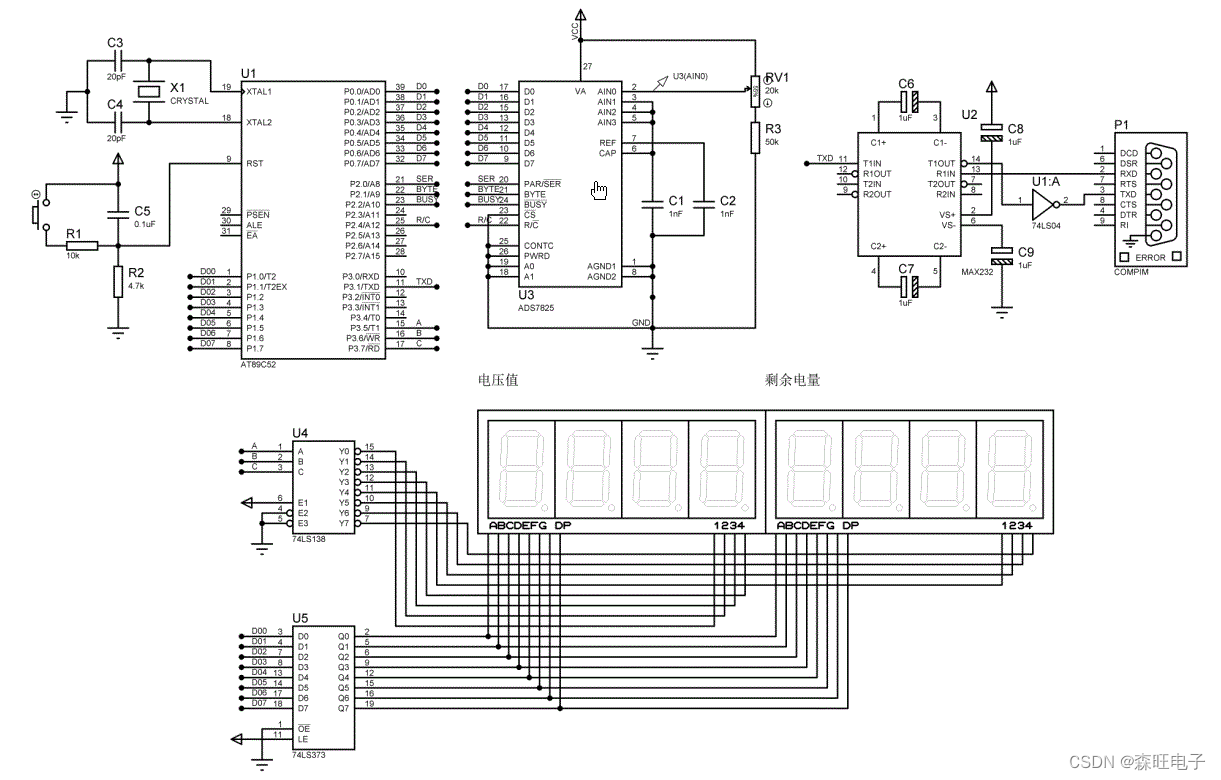
3.下位机程序

4.显示
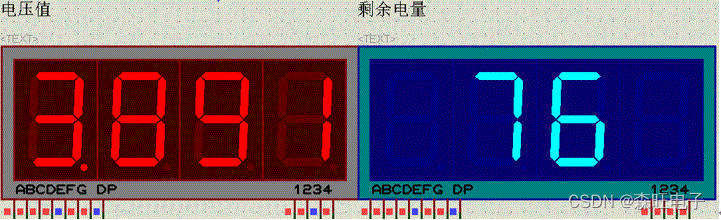
5.上位机界面

6.上位机程序
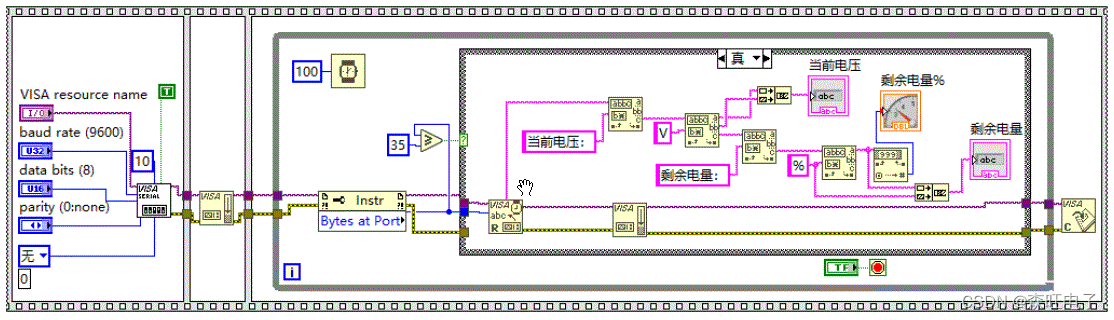
7.文档

注意:文件夹(5)中,包含了word格式的文档,以及部分报告中用图,其中(流程图.eddx)需要使用(亿图)软件打开,Proteus原理图工程的dsn文件要用Proteus7.5版本打开

:探索人工智能领域的新边界)
![[C++]让C++的opencv库支持写出h264格式视频](http://pic.xiahunao.cn/[C++]让C++的opencv库支持写出h264格式视频)
分析)



![[Linux基础]ln硬链接和ln -s软链接的方法参数及区别](http://pic.xiahunao.cn/[Linux基础]ln硬链接和ln -s软链接的方法参数及区别)











