二叉树是指度为 2 的树。它是一种最简单却又最重要的树,在计算机领域中有这广泛的应用。
二叉树的递归定义如下:二叉树是一棵空树,或者一棵由一个根节点和两棵互不相交的分别称为根节点的左子树和右子树所组成的非空树,左子树和右子树同样都是一棵二叉树。在二叉树中,每个节点的左子树的根节点被称为左孩子节点,右子树被称为右孩子节点。
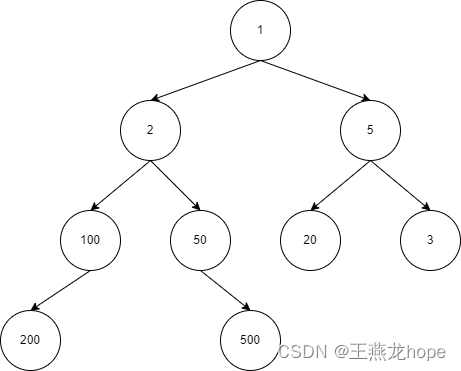
二叉树通常使用如下数据结构来表示:
data 表示二叉树节点的数值,left_child 表示节点的左孩子节点,right_child 表示节点的右孩子节点。
struct node {int data;struct node *left_chile;struct node *right_child;
}从二叉树的定义来看,有以下两点;
(1) 二叉树可以是一棵空树
(2) 二叉树的左子树和右子树不一定存在,可能同时不存在,可能同时存在,也可能左子树和右子树只存在一个
为什么要有二叉树 ?
在我们使用数据结构来存储数据的时候,最常见的两个使用场景是查找和插入。查找就是从数据结构中找到我们想要的值,插入是将一个新值插入到数据结构正确的位置。
在数据结构中,最常用的两个基础的数据结构是数组和链表,数组和链表的区别可以从如下 3 个方面来看:
① 插入元素。数组的插入效率比链表低,因为数组插入的时候,插入位置后边的元素都要向后移动;而向链表中插入元素的时候,只需要改变节点的指向就可以。前者的时间复杂度是 O(n) 的,后者的时间复杂度是 O(1) 的。
② 读取元素。读取数组中的第几个元素的时候,使用数组的下标直接读取就可以,而读取链表中的第几个元素的时候,需要对链表进行遍历。前者的时间复杂度是 O(1) 的,后者的时间复杂度是 O(n) 的。
③ cache。数组用一块连续的内存来维护,链表中每个节点的地址并不连续。从 cpu cache LRU 算法的角度来看的话,数组中的元素离的更近,所以访问性能会更高。
从数组和链表的对比来看,没有哪种数据结构是具备所有的优点的。
二叉树有 3 个重要的变种,分别是二叉排序树,二叉平衡树,红黑树。
(1)二叉排序树
二叉排序数是一棵特殊的二叉树,在一般的二叉树中,区分左子树和右子树,但结点的值是无序的。在二叉排序树中,不仅区分左子树和右子树,而且整个树的节点是有序的。
二叉排序树又称二叉搜索树,它或者是一棵空树,或者是一棵非空二叉树,具备如下 3 个特点:
① 如果左子树非空,那么左子树上所有节点的值小于根节点的值
② 如果右子树非空,那么右子树上所有节点的值大于根节点的值,如果允许节点的值相等,那么大于等于
③ 左、右子树本身又各是一棵二叉排序树
从分析可以得出,在查找的性能上,二叉排序树的时间复杂度是 O(logn),相对于链表的 O(n),是有优化的。但是二叉排序树最差的情况,是每个节点都只包含一个子节点,这种情况下的时间复杂度就成为了 O(n),所以在二叉排序树的基础上出现了二叉平衡树。
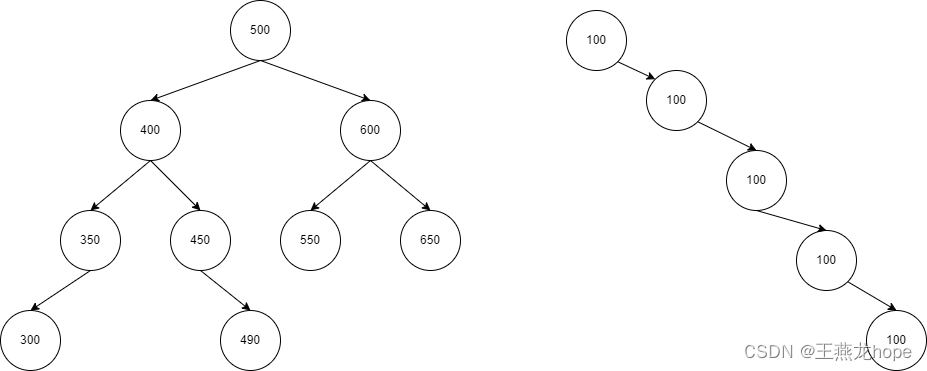
(2)二叉平衡树
二叉平衡树首先是一颗二叉排序树,在此基础上又增加了一个条件,即每个节点的左子树和右子树的高度之差不大于 1。
有了这个限制之后,查找的时间复杂度就不会出现 O(n) 的情况。但是当向平衡树中插入元素的时候,为了保证插入之后二叉树还能满足平衡树的要求,需要进行旋转操作。对于频繁插入,删除的场景,旋转操作过于频繁,反而会增加时间的消耗。所以出现了红黑树,红黑树在查找和插入操作之间取得了平衡(这样的结论,只有专门研究红黑树算法的专业人员才能了解,在很多文章和书籍中也是这么说的,我们只需要知道这个事情即可)。
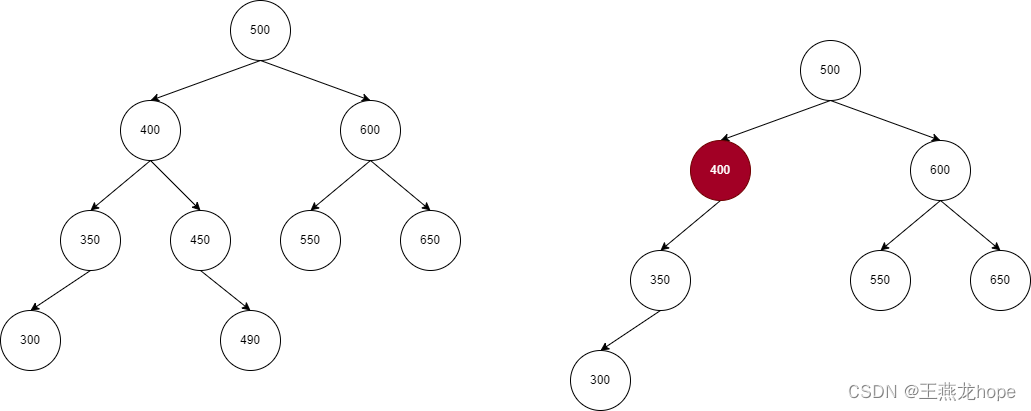
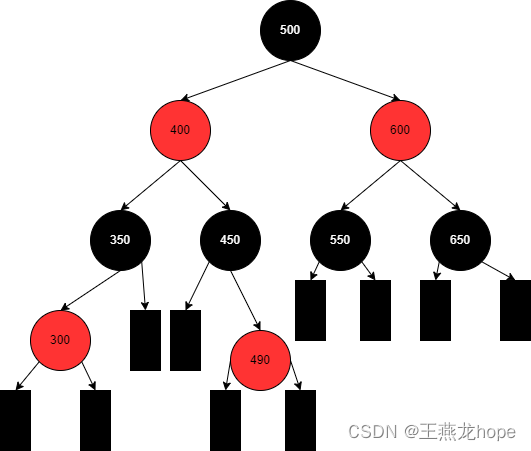
(3)红黑树
红黑树的前提也是一颗二叉排序,在此基础上增加了以下 5 个条件:
① 红黑树中的节点要么是黑色,要么是红色
② 红黑树的根节点是黑色
③ 红黑树中红色节点不能连续,也就是说一个红色节点的父节点和子点都不能是红色
④ 从根节点开始,到叶子节点,每条路径上的黑色节点个数相等
⑤ 叶子节点是黑色,在红黑树中的叶子结点不是真实存在的,叶子结点在下图中用矩形来表示
在工程应用中,本人还没见过使用平衡树的场景,只见过使用红黑树的场景。
① 在 linux 内核中,维护 struct task_struct 使用了红黑树;维护 tcp 接收侧的乱序队列,使用了红黑树;epoll 中维护监听的 fd,也是用了红黑树
② 在 c++,java 内置的 map 数据结构中,使用了红黑树
本文只记录二叉树的基本算法,不涉及二叉排序树,二叉平衡树,红黑树相关的算法。
1 二叉树遍历
二叉树的遍历有 4 中算法:前序遍历,中序遍历,后序遍历以及层序遍历。前 3 种遍历算法中的前、中、后,说的是根节点的位置:前序遍历的顺序是根节点,左子节点,右子节点;中序遍历的顺序是左子节点,根节点,右子节点;后序遍历的顺序是左子节点,右子节点,根节点。不管哪种遍历,左子节点都在右子节点之前遍历。
如果了解图的遍历算法,可以知道图的遍历算法包括两种:深度优先遍历和广度优先遍历。二叉树的遍历方法中,前 3 种类似于图中的深度优先遍历,层序遍历类似于广度优先遍历。
二叉树跟递归算法联系比较紧密,递归算法有两点组成,一个是递归退出条件,一个是递归计算逻辑,也可以称为递归体,这一点和循环是有点相似的,循环也要有循环停止条件和循环处理逻辑。每种算法的对象都是围绕着一个数据结构,都需要有一个驱动力,这个驱动力往往就是对数据结构中的元素进行遍历,对于数组来说往往就是沿着数组下标进行遍历,对于链表来说往往就是从 head 开始沿着 next 向下遍历,对于二叉树来说就是沿着 left child 和 right child 进行遍历。对数据进行遍历是算法的基础。
递归算法,不太适合从一开始沿着算法逐渐向下思考,使用递归算法的时候我们可以使用一个最简单的场景来理解。比如,对于二叉树来说,我们以只有 3 个节点(一个 root,一个 left child,一个 right child)的二叉树来思考和理解。
1.1 前序遍历
力扣:. - 力扣(LeetCode)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {if (root == nullptr) {return ret;}preScan(root);return ret;}void preScan(TreeNode *root) {ret.push_back(root->val);if (root->left) {preScan(root->left);}if (root->right) {preScan(root->right);}}private:vector<int> ret;
};1.2 中序遍历
力扣:. - 力扣(LeetCode)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {if (root == nullptr) {return ret;}midScan(root);return ret;}void midScan(TreeNode *root) {if (root->left) {midScan(root->left);}ret.push_back(root->val);if (root->right) {midScan(root->right);}}private:vector<int> ret;
};1.3 后续遍历
力扣:. - 力扣(LeetCode)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {if (root == nullptr) {return ret;}postScan(root);return ret;}void postScan(TreeNode *root) {if (root->left) {postScan(root->left);}if (root->right) {postScan(root->right);}ret.push_back(root->val);}private:vector<int> ret;
};1.4 层序遍历
力扣:. - 力扣(LeetCode)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {std::queue<TreeNode *> q;std::vector<vector<int>> ret;if (root == nullptr) {return ret;}q.push(root);while (!q.empty()) {// 用来保存二叉树一层的数据// 如果只是遍历,不用保存数据的话,那么是用不着这个数据结构的vector<int> line;int q_size = q.size();for (int i = 0; i < q_size; i++) {TreeNode *node = q.front();q.pop();line.push_back(node->val);if (node->left) {q.push(node->left);}if (node->right) {q.push(node->right);}}ret.push_back(line);}return ret;}
};2 二叉树遍历的应用
2.1 求二叉树高度
力扣:. - 力扣(LeetCode)
求二叉树的高度,也是使用递归算法。有两种算法:
(1)求出左子树和右子树的高度,然后两者的较大值加 1 就是二叉树的高度
(2)使用动态规划的算法,每一次递归计算的时候,相当于向下增加了一层,在递归函数的形参中实时维护已经遍历的二叉树的高度,二叉树遍历完之后,最大值保存的就是二叉树的高度
2.1.1 左子树和右子树较大值
int maxDepth(struct TreeNode* root) {if (root == NULL) {return 0;}int left_height = 0;int right_height = 0;if (root->left) {left_height = maxDepth(root->left);}if (root->right) {right_height = maxDepth(root->right);}if (left_height > right_height) {return 1 + left_height;} else {return 1 + right_height;}
}2.1.2 动态规划
class Solution {
public:int maxDepth(TreeNode* root) {maxDepthHelper(root, 0);return max_depth_;}void maxDepthHelper(TreeNode *root, int depth) {if (root == nullptr) {return;}depth++;if (depth > max_depth_) {max_depth_ = depth;}if (root->left) {maxDepthHelper(root->left, depth);}if (root->right) {maxDepthHelper(root->right, depth);}}private:int max_depth_ = 0;
};2.2 求二叉树宽度
求二叉树的宽度和求二叉树的高度,算法是类似的,都可以通过动态规划的方式来进行。
在递归函数中用一个形参实时表示当前遍历的是哪一层的节点,每遍历一个节点都将这一层的宽度加 1。使用一个数组保存每一层的宽度,遍历结束之后,再遍历数组找到宽度最大的这一层。
class Solution {
public:int maxWidth(TreeNode* root) {maxWidthHelper(root, 0);for (int i = 0; i < max_depth_; i++) {if (width[i] > max_width_) {max_width_ = width[i];}}return max_width_;}void maxDepthHelper(TreeNode *root, int depth) {if (root == nullptr) {return;}width[depth] = width[depth] + 1;depth++;if (depth > max_depth_) {max_depth_ = depth;}if (root->left) {maxWidthHelper(root->left, depth);}if (root->right) {maxWidthHelper(root->right, depth);}}private:int max_width_ = 0;int max_depth_ = 0;int width[100] = {0}; // 定义一个保存每一层宽度的数组,假设二叉树的高度不会超过 100
};2.3 二叉树路径
力扣:. - 力扣(LeetCode)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<string> binaryTreePaths(TreeNode* root) {tmp_data_path.push_back(root->val);binaryTreeScan(root);return ret;}void binaryTreeScan(TreeNode *root) {if (root->left == nullptr && root->right == nullptr) {string str_path = makePath();ret.push_back(str_path);return;}if (root->left) {// 使用递归算法找路径的典型代码// 三段式:push back --> 递归运算 --> pop back// 为什么递归运算结束之后,需要将元素 pop 出来// 因为通过递归算法,和这个节点相关的路径都已经遍历到了// 后边再遍历的路径,与这个节点无关了,所以需要把这个节点 pop 出来// 以防影响后边的路径// 图的遍历找路径的算法题中,主要的递归逻辑也是类似的tmp_data_path.push_back(root->left->val);binaryTreeScan(root->left);tmp_data_path.pop_back();}if (root->right) {tmp_data_path.push_back(root->right->val);binaryTreeScan(root->right);tmp_data_path.pop_back();}}string makePath() {int size = tmp_data_path.size();std::string str;for (int i = 0; i < size; i++) {if (i < size - 1) {str += std::to_string(tmp_data_path[i]) + "->";} else {str += std::to_string(tmp_data_path[i]);}}return str;}private:vector<string> ret;vector<int> tmp_data_path;
};2.4 二叉树翻转
力扣:. - 力扣(LeetCode)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == nullptr) {return root;}binaryTreeScan(root);return root;}void binaryTreeScan(TreeNode *root) {TreeNode *left = root->left;root->left = root->right;root->right = left;if (root->left) {binaryTreeScan(root->left);}if (root->right) {binaryTreeScan(root->right);}}
};

)










数据)




![华为OD-C卷-小明找位置[100分]](http://pic.xiahunao.cn/华为OD-C卷-小明找位置[100分])
