我们可以写一个卷积算法。

for (int oh = 0; oh < OH; oh++) {for (int ow = 0; ow < OW; ow++) {for (int oc = 0; oc < OC; oc++) {C[oh][ow][oc] = 0;for (int kh = 0; kh < KH, kh++){for (int kw = 0; kw < KW, kw++){for (int ic = 0; ic < IC, ic++){C[oh][ow][oc] += A[oh+kh][ow+kw][ic] * B[kh][kw][ic];}}}}}
}

这种很显然是一个典型的卷积算法。

首先，最经典的算法是im2col算法。

计算完成后，会变成左图所示计算：

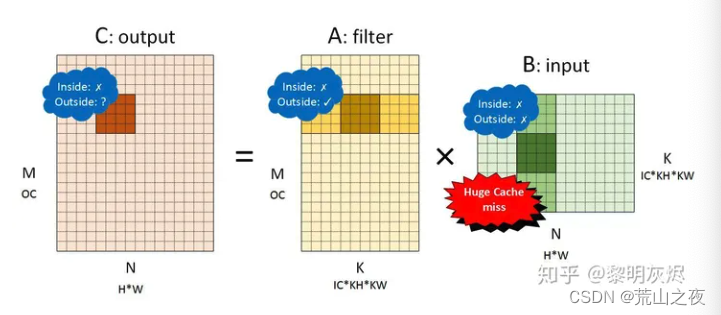这个计算的逻辑，大家可以看这一篇文章来进行理解。

但是对于输出而言，这并不是一个好的排布，因为内存访问局部差。为啥？因为你先把内存整成这个样子。其实你访问行，效果当然会好很多。

对于kernel而言，当然是有利的，因为一次加载一行。起码这一行都是可以用到的。

对于feature_map来说，这样算，就不是很OK了叭。每一次都要去内存取数据。

所以，NCHW，对内存不是很友好。【其实我并没有感觉到有多不友好】

然后，使用NHWC的时候。

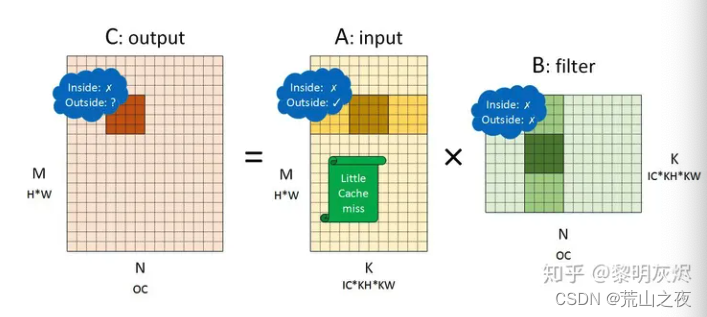
那我们继续向我们的计算方式。从NCHW结构，转为NHWC结构。

那么，注意看，这里是input * filter了。

可以参考下图的一个变换：

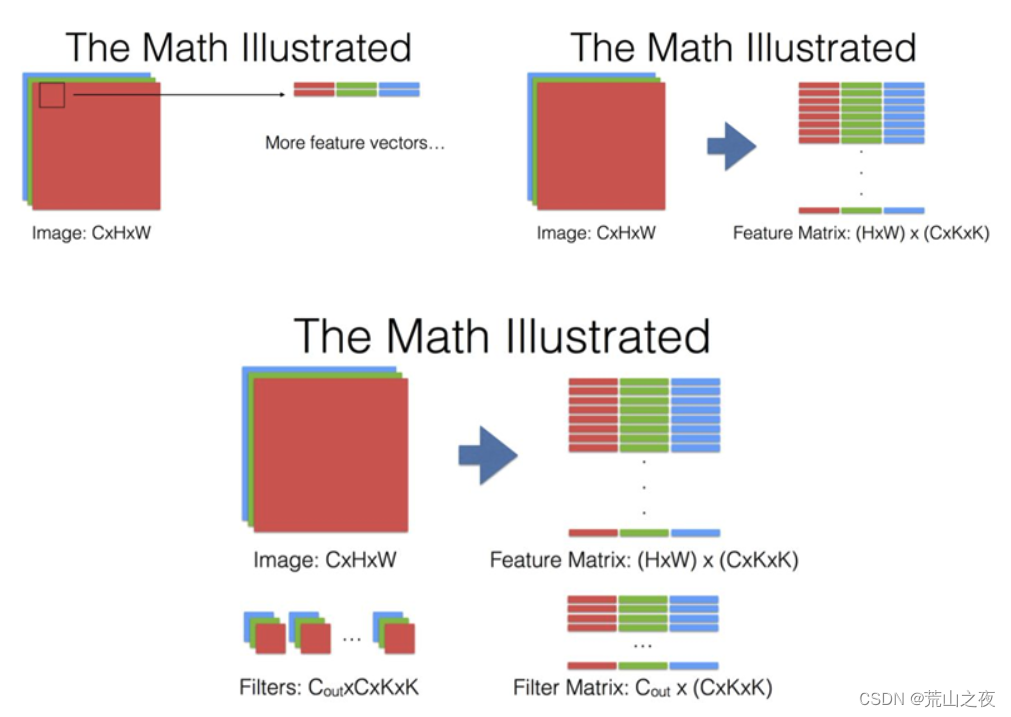
HWC，不管C是怎么样的，那么filter，理论上是K*K*C。对于某一个点，是不是要进行乘法。

那么把结构平铺一下，就是：H*W*C 到 K*K*C

如果结构是：

CHW,那最后输出的结果是：OC,H,W的排布。

那么变成二维，就是OC*HW，为了算一个点的OC，我们需要对一个点，和所有相关的filter过一遍。也就是说：大概是把kernel进行复制，从一个点，复制到[oc * HW]  

那么filter的排布就是： oc ic H W

同理， feature map的排布是：ic,H,W

这个时候要算，就要oc摘出来，变成oc *H W = oc * icHW dot icHW,

那么为了性能优化， 我们可以对feature map进行倍化，先把kernel需要的数量给凑够了。

比如feature map 变成oc H W IC  K K ,这样的话，kernel就是： ic k k  oc, 这样起码改了kernel的排布。

这样的话，计算结果，最后只要把K*K给加起来就好了。

这个过程很复杂，可能得一会儿想。

然后，oc h w这种排布，因为输出是这样排布的。oc,H,w,

但如果是h w co这样排布呢？

那就是HW-OC = HW-oc-kwkhic  dot HW-oc