【LeetCode】二叉树类题目详解

image-20240308204329883

二叉树

二叉树的理论基础

二叉树是结点的度数之和不超过2的树，二叉树总共有五种基本形态

二叉树的种类主要有：

  • 满二叉树
  • 完全二叉树

二叉树的存储方式

  • 顺序存储
  • 链式存储

二叉树的遍历方式

  • 先序遍历（深度优先搜索）
  • 中序遍历（深度优先搜索）
  • 后序遍历（深度优先搜索）
  • 层次遍历（广度优先搜索）

对于二叉树结点的定义：

class TreeNode:def __init__(self, val, left = None, right = None):self.val = valself.left = leftself.right = right

二叉树的递归遍历

先序遍历

class Solution:def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root:return []return [root.val] + self.preorderTraversal(root.left) + self.preorderTraversal(root.right)

中序遍历

class Solution:def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root:return []return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right)

后续遍历

class Solution:def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root:return []return self.postorderTraversal(root.left) + self.postorderTraversal(root.right) + [root.val]

image-20231102203600726

二叉树的非递归遍历

先序遍历

方法1：利用栈先进后出的性质，先把右孩子结点放入栈中，再将左孩子结点放入栈中，这样就可以先访问根节点， 在访问左孩子，最后访问右孩子了。

class Solution:def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root:return []stack = [root]res = []while stack:node = stack.pop()# print(node)res.append(node.val)if node.right:stack.append(node.right)if node.left:stack.append(node.left)return res

方法2：按照中序遍历的算法，只需要将添加append操作放到前面去即可。但需要控制两个指针。

思路：沿着左子树一直往左下方走，左孩子不为空就一直进栈，同时将其值添加到res列表中。如果左孩子为空，则弹出栈顶元素，然后再访问该结点的右孩子，再重复上述的操作直到遍历结束。

class Solution:def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root:return []stack = []res = []cur = rootwhile cur or stack:if cur:stack.append(cur)res.append(cur.val)cur = cur.leftelse:cur = stack.pop()cur = cur.rightreturn res

中序遍历

中序遍历参考先序遍历思路2，区别就是只需要append语句放到当cur指针为空的时候里面。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root:return []stack = []res = []cur = rootwhile cur or stack:if cur:stack.append(cur)cur = cur.leftelse:cur = stack.pop()res.append(cur.val)cur = cur.rightreturn res

image-20231102203511759

后序遍历

思路：在进行先序遍历的时候，我们的思路是利用栈，首先访问根结点，然后将右子树添加到栈中，再将左子树添加到栈中，实现的效果是根左右的效果，而在进行后序遍历的时候，我们需要的的顺序是左右根，如果我们先序遍历算法中左右子树进栈的顺序修改之后，刚好可以得到我们后续遍历结果的逆序结果，最终的返回值设置为res[::-1]即为最终答案。

class Solution:def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if not root:return []stack = [root]res = []while stack:node = stack.pop()# 根 右 左res.append(node.val)if node.left:stack.append(node.left)if node.right:stack.append(node.right)# 左 右 根return res[::-1]

层次遍历

层次遍历需要借助队列来实现，队列先进先出的特点可以很好的满足层次遍历按层遍历的需要。

代码模板（以力扣为标准）

image-20231102193339525

class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if not root:return []queue = [root]res = []while queue:tmp = []for _ in range(len(queue)):node = queue.pop(0)tmp.append(node.val)if node.left:queue.append(node.left)if node.right:queue.append(node.right)res.append(tmp)return res

image-20231102193628125

上面的代码还可以进行优化，Python中列表在进行pop(0)的时候，需要移动后面的元素，会导致时间复杂度变高，可以在用collections类中提供的双端队列deque来方便在队头队尾进行元素的插入和删除。

class Solution:def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if not root:return []res = []queue = deque([root])while queue:tmp = []for _ in range(len(queue)):node = queue.popleft()tmp.append(node.val)if node.left:queue.append(node.left)if node.right:queue.append(node.right)res.append(tmp)return res
  • list：和添加操作类似，从list尾部移除（pop）元素是很快的，时间复杂度为O(1)。但从头部移除（pop(0)）元素则时间复杂度为O(n)。
  • deque：deque同样能够在两端移除元素，无论是popleft还是pop，时间复杂度都是O(1)。

这点在进行N叉树的层次遍历的时候可以体现的比较明显

429、N叉树的层次遍历

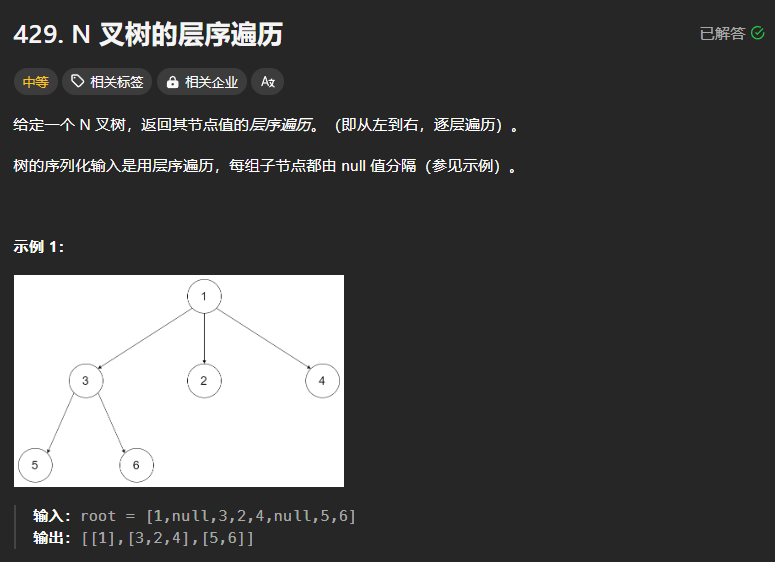
image-20231208170548739

class Solution:def levelOrder(self, root: 'Node') -> List[List[int]]:if not root:return []# 使用双端队列存放queue = deque([root])res = []while queue:tmp = []for _ in range(len(queue)):node = queue.popleft()tmp.append(node.val)# N叉树 遍历孩子结点 ，孩子结点是一个可以迭代的对象for child in node.children:queue.append(child)res.append(tmp)return res

image-20231208170444573

1609、奇偶数

image-20231208171744921

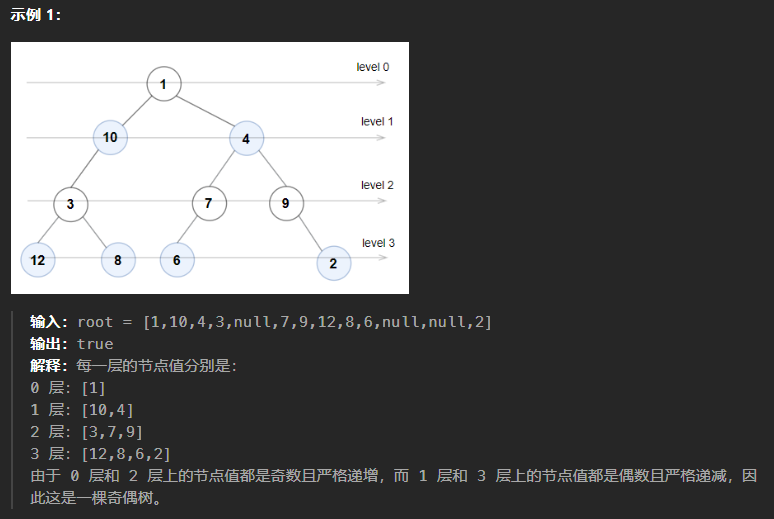
image-20231208171756572

本题可以直接使用层次遍历，在遍历的过程中使用pre记录前一个结点，然后两个结点相减如果不满足题目的要求则返回false，在层次遍历的过程中用tag记录当前遍历的层数，如果层数和对应的数字奇偶不符，也返回False，直到程序运行结束返回True

class Solution:def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:# 树中节点数至少为1  不用判断树为空的情况queue = deque([root])tag = 0  # 用于判断层数while queue:pre = float("-inf") if tag%2==0 else float("inf")for _ in range(len(queue)):node = queue.popleft()if tag%2==0:if node.val%2==0 or node.val-pre<=0:return Falseelse:if node.val%2==1 or node.val-pre>=0:return Falsepre = node.valif node.left:queue.append(node.left)if node.right:queue.append(node.right)tag+=1return True

本题中，使用list和使用deque的性能差别是非常明显的。

image-20231208172036534

二叉树的层次遍历可以衍生出非常多的变种题目。

  • 102.二叉树的层序遍历(opens new window)
  • 107.二叉树的层次遍历II(opens new window)
    • 本题和层次遍历的区别就是只需要返回res列表的逆序即可。
  • 199.二叉树的右视图(opens new window)
  • 637.二叉树的层平均值(opens new window)
  • 429.N叉树的层序遍历(opens new window)
  • 515.在每个树行中找最大值(opens new window)
  • 116.填充每个节点的下一个右侧节点指针(opens new window)
  • 117.填充每个节点的下一个右侧节点指针II(opens new window)
  • 104.二叉树的最大深度(opens new window)
  • 111.二叉树的最小深度

199、二叉树的右视图

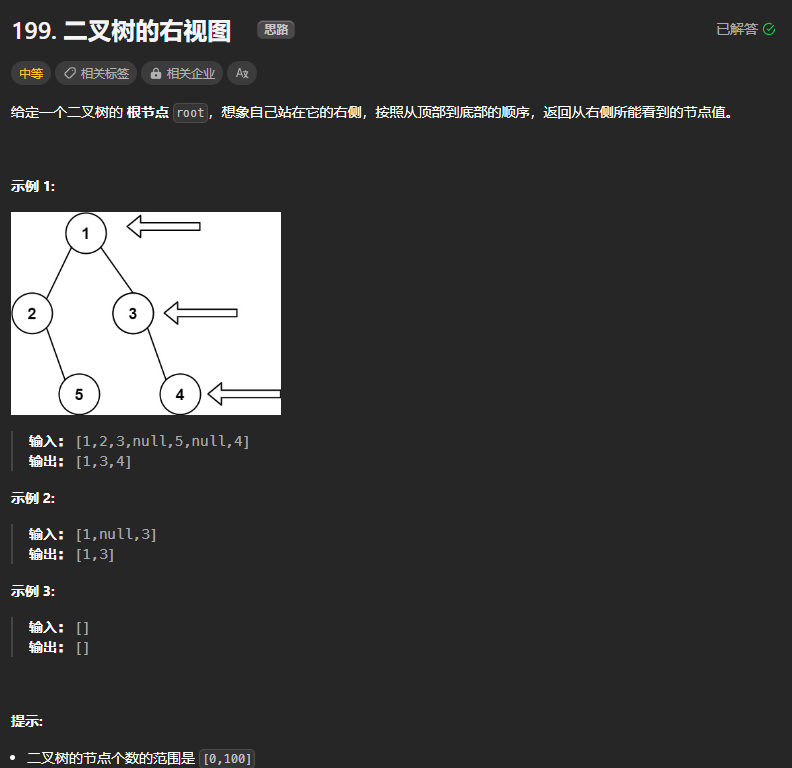
image-20231103101656058

class Solution:def rightSideView(self, root: Optional[TreeNode]) -> List[int]:if not root:return []queue = [root]res = []while queue:tmp = 0for _ in range(len(queue)):node = queue.pop(0)# tmp.append(node.val)if node.left:queue.append(node.left)if node.right:queue.append(node.right)tmp = node.valres.append(tmp)return res

image-20231103101640796

使用双端队列

class Solution:def rightSideView(self, root: Optional[TreeNode]) -> List[int]:if not root:return []queue = deque([root])res = []while queue:tmp = 0for _ in range(len(queue)):node = queue.popleft()if node.left:queue.append(node.left)if node.right:queue.append(node.right)tmp = node.valres.append(tmp)return res

image-20240313130123171

111、二叉树的最小深度

image-20231106095458959

本题的解题思路与二叉树的最大深度大同小异，唯一的区别就是在循环中进行判断当前节点的左右孩子结点是否为空，如果为空，则直接返回depth即可，如果不为空就一直进行循环，最后再返回depth，代码的主体框架与层次遍历是一致的。

# 层次遍历
class Solution:def minDepth(self, root: Optional[TreeNode]) -> int:if not root:return 0queue = [root]depth = 0while queue:depth+=1for _ in range(len(queue)):node = queue.pop(0)if node.left:queue.append(node.left)if node.right:queue.append(node.right)if not node.right and not node.left:return depthreturn depth

层次遍历时间

103、二叉树的锯齿形层序遍历

image-20240313123714590

image-20240313123730174

本题需要使用2个双端队列，一个用来存放树的结点，一个用来存放每一层的结点，用双端队列就是方便在队头和对尾进行插入。利用collections模块中的deque的方法：

  • appendleft()：在队头进行插入
  • append()：在队尾进行插入
  • pop()：删除队尾的元素
  • popleft()：删除队头的元素

由于tmp是属于双端队列类型的，需要再最后往res数组中存放的时候，强制转换为list类型。

class Solution:def zigzagLevelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:if not root:return []res = []queue = deque([root])flag = 0while queue:tmp = deque()for _ in range(len(queue)):node = queue.popleft()if flag % 2 == 0:tmp.append(node.val)else:tmp.appendleft(node.val)if node.left:queue.append(node.left)if node.right:queue.append(node.right)res.append(list(tmp))flag += 1return res

image-20240313124031559

637、二叉树的层平均值

image-20240313124823462

image-20240313124836239

class Solution:def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:res = []queue = deque([root])while queue:sum_ = 0count = 0for _ in range(len(queue)):node = queue.popleft()sum_ += node.valcount += 1if node.left:queue.append(node.left)if node.right:queue.append(node.right)res.append(sum_ / count)return res

二叉树的深度与高度

二叉树的深度与高度有一些区别，其中二叉树中的深度是指从根结点到该节点的路径长度。高度是指从叶子结点到当前结点的路径长度。

结点的深度是从根结点开始自顶向下逐层累加的。

结点的高度是从叶子结点开始自底向上逐层累加的。

在力扣中有几道题目是与二叉树的深度相关，一般而言如果是需要求深度的，都采用先序遍历的方法，因为先序遍历先遍历根结点，然后遍历孩子结点就可以得出其深度。满足其自顶向下的特点。一般而言可以采用递归方法。

深度：先序遍历 | 层次遍历

高度：后续遍历

  • 104.二叉树的最大深度
  • 559.n叉树的最大深度
  • 111.二叉树的最小深度

根结点的高度就是二叉树的最大深度。

104、二叉树的最大深度

image-20231113191706720

求最大深度，需要从根结点开始自定向下进行深度优先搜索DFS，因此采用先序遍历，采用递归的实现方式

class Solution:def maxDepth(self, root: Optional[TreeNode]) -> int:# 先序遍历求最大深度 根左右   深度是从根节点到最后  高度是从叶子结点到当前节点的高度if not root:return 0left_height = self.maxDepth(root.left)right_height = self.maxDepth(root.right)height = 1 + max(left_height,right_height)return height

其中代码还可以精简为

class Solution:def maxDepth(self, root: Optional[TreeNode]) -> int:if not root:return 0return 1+max(self.maxDepth(root.left),self.maxDepth(root.right))

image-20231113192723426

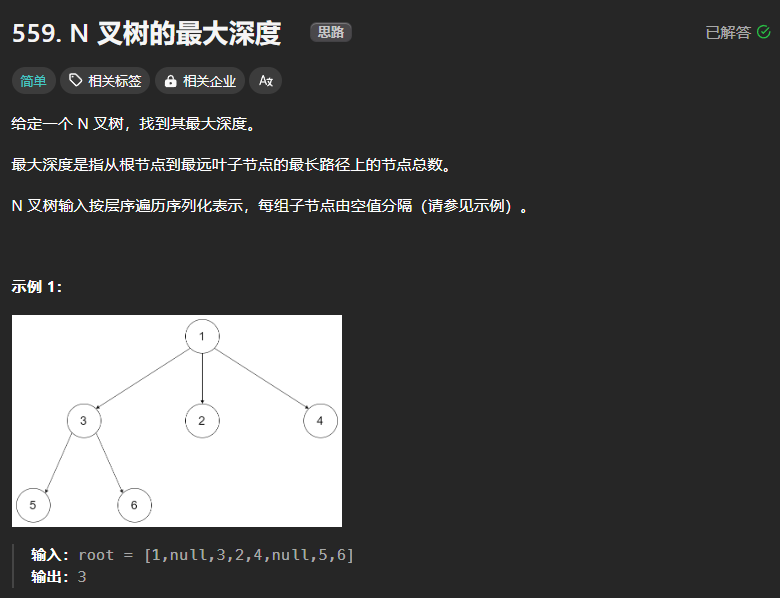
559、n叉树的最大深度

image-20231113192558344

解题思路与二叉树的最大深度一致，唯一的区别就是通过for循环去遍历孩子结点

"""
# Definition for a Node.
class Node:def __init__(self, val=None, children=None):self.val = valself.children = children
"""class Solution:def maxDepth(self, root: 'Node') -> int:if not root:return 0max_depth = 0for ch in root.children:max_depth = max(max_depth,self.maxDepth(ch))return 1+max_depth

image-20231113192704871

111、二叉树的最小深度

image-20231113192853117

解题思路和求最大深度差不多，但是又有一个特殊情况，就是当二叉树为单分支的情况，即当出现某个节点的左孩子或者右孩子其中之一为空的时候，深度就要取最右孩子中的最大值了，否则就会结果为0+1。其余的情况就取最小值即可。

class Solution:def minDepth(self, root: Optional[TreeNode]) -> int:if not root:return 0left_depth = self.minDepth(root.left)right_depth = self.minDepth(root.right)if not root.left or not root.right:return 1+max(left_depth,right_depth)return 1+min(left_depth,right_depth)

特殊的二叉树

完全二叉树

补充：

110、平衡二叉树

平衡二叉树的定义是左右子树的高度之差不超过1的二叉树。

image-20231113193458877

代码

定义一个获取结点高度的函数get_height()，如果当前结点为空，则返回0，然后分别获取该结点左孩子和右孩子的高度，如果左右孩子高度返回值是-1，则也返回-1，否则在判断左右子树高度之差是否大于1，如果大于1则也返回-1，如果左右子树高度之差小于1，则返回1+max(left_height, right_height)。主程序中，只需要判断对根节点进行判断get_height(root)是否为-1即可判断该二叉树是否是平衡二叉树。

class Solution:def isBalanced(self, root: Optional[TreeNode]) -> bool:def get_height(root):if not root:return 0left_height = get_height(root.left)if left_height==-1:return -1right_height = get_height(root.right)if right_height==-1:return -1if abs(left_height-right_height)>1:return -1else:return 1+max(left_height,right_height)return True if get_height(root)!=-1 else False

image-20231114193151177

二叉排序树

练习题

116、翻转二叉树

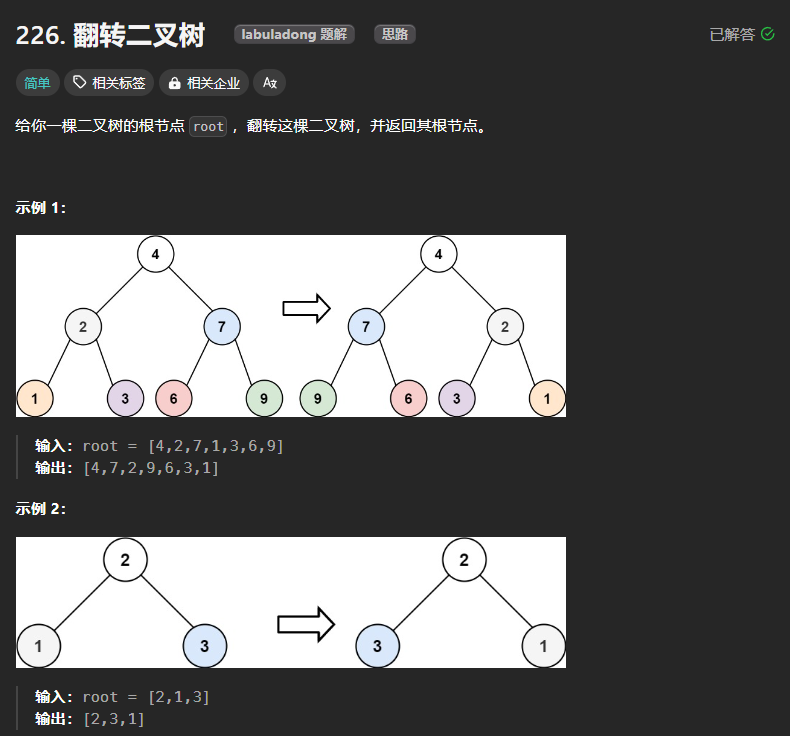
image-20231114134848424

由示例可以看出，本题实际上需要实现的功能是沿着中间的一个轴翻转这颗二叉树，其本质实际只需要将二叉树每个结点的左右子树进行翻转即可。

翻转二叉树的核心思想就是：将二叉树中的每个节点的左右孩子进行交换即可。

需要注意的是，本题不能采用中序遍历的方法，可以采用先序遍历或者后序遍历

class Solution:def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:if not root:return rootself.invertTree(root.left)self.invertTree(root.right)root.left,root.right = root.right,root.leftreturn root

中序遍历的时候可能会对一些节点重复的调换导致错误。

image-20231114144227076

class Solution:def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:# 采用后序遍历if not root:return rootleft = self.invertTree(root.left)right = self.invertTree(root.right)root.left,root.right = right,leftreturn root

image-20231223191938312

101、对称二叉树

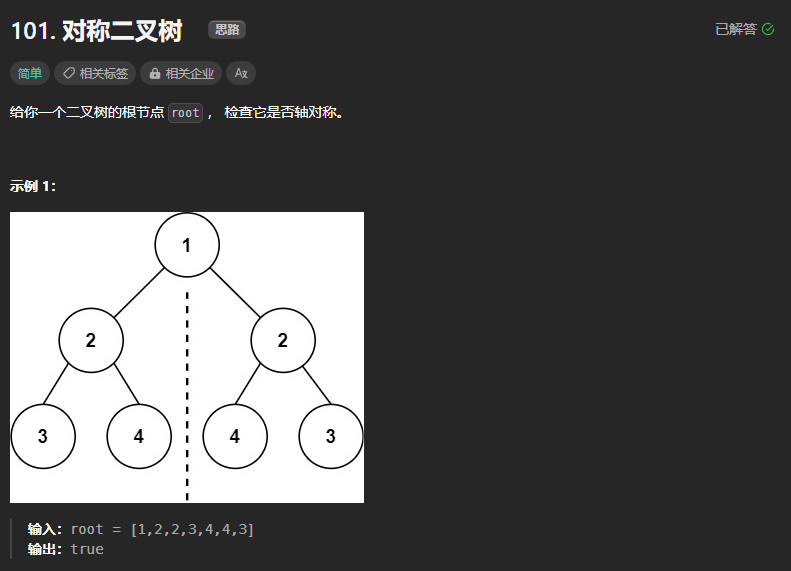
image-20231103111251882

本题思路与翻转二叉树有点区别，翻转二叉树是直接对比左右孩子结点的值是否相等即可判断，而本题需要判断的是（例如在第三层中，判断根节点左孩子2的左孩子是否与根结点右孩子2的右孩子是否相等）对比的其实是外侧与外侧，内侧与内侧。

class Solution:def isSymmetric(self, root: Optional[TreeNode]) -> bool:def compare(left,right):if left and not right: return Falseelif not left and right: return Falseelif not left and not right: return Trueelif left.val != right.val: return Falseout = compare(left.left,right.right)inner = compare(left.right,right.left)return out and innerif not root:return Truereturn compare(root.left,root.right)

100、相同的树

image-20231114152650867

思路基本与对称二叉树一致，需要对两棵树的结点的值以及左右子树的值进行对比，如果不相同则返回，相等则继续递归，知道递归结束。

class Solution:def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:if not p and not q: return Trueelif not p or not q: return Falseelif p.val!=q.val: return Falsereturn self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)

image-20231114152707949

572、另一棵树的子树

image-20231114151903739

解题思路与相同的树一致，只需要遍历root这棵树的每个结点，然后再与subRoot进行判断是否是相同的树即可。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:def isSame(s,t):if not s and not t:return Trueelif not s or not t:return Falseelif s.val!=t.val:return Falsereturn isSame(s.left,t.left) and isSame(s.right,t.right)# 遍历root的所有结点与subRoot进行比较if not root:return Falsestack = [root]while stack:node = stack.pop()if isSame(node,subRoot):return Trueif node.left:stack.append(node.left)if node.right:stack.append(node.right)return False

image-20231114152036046

222、完全二叉树的节点数量

image-20231106104412026

解题思路1：可以直接按照普通二叉树的遍历进行记录总共多少个结点（前中后序遍历+层次遍历都可以解决这个问题），时间复杂度为 O(n)

（此方法没有利用完全二叉树的性质）

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def countNodes(self, root: TreeNode) -> int:if not root:return 0return 1 + self.countNodes(root.left) + self.countNodes(root.right)

image-20231106104634852

使用层次遍历

class Solution:def countNodes(self, root: Optional[TreeNode]) -> int:if not root:return 0num = 0queue = [root]while queue:for _ in range(len(queue)):num+=1node = queue.pop(0)if node.left:queue.append(node.left)if node.right:queue.append(node.right)return num

image-20231114193418762

解题思路2：利用完全二叉树的性质，如果是满二叉树结点的数量可以用2的深度-1次方 再 -1 来进行计算。时间复杂度为O(logn * logn)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def countNodes(self, root: TreeNode) -> int:if not root:return 0left = root.leftright = root.rightleftdepth = 0rightdepth = 0while left:leftdepth+=1left=left.leftwhile right:rightdepth+=1right=right.rightif leftdepth==rightdepth:return (2<<leftdepth)-1leftnum = self.countNodes(root.left)rightnum = self.countNodes(root.right)return leftnum+rightnum+1

image-20231106104900697

257、二叉树的所有路径

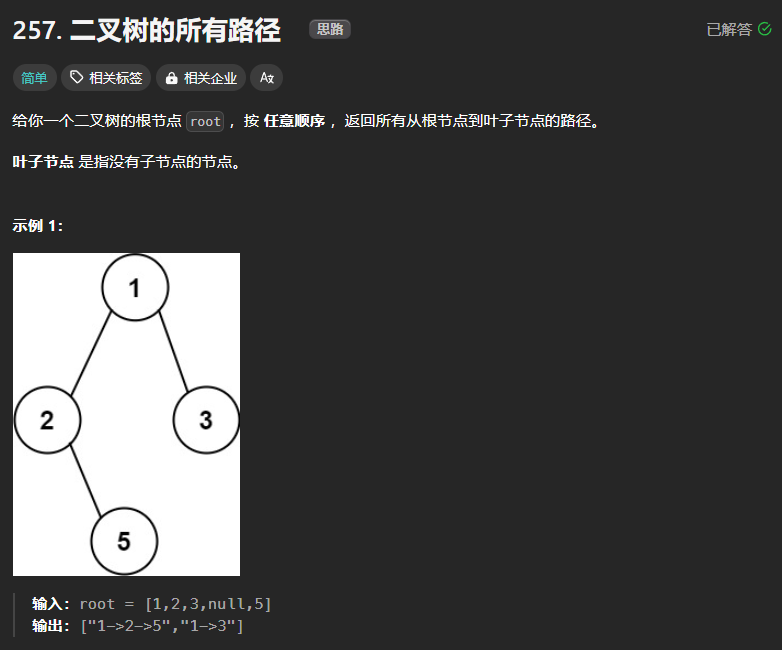
image-20231114155412077

本题使用DFS与BFS均可解决。

使用DFS的时候需要注意在递归的过程中如果当前结点为空则不进行处理，不为空时才进行处理。

class Solution:def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:# 使用DFS解决def find_path(node,path):# node结点不为空if node:path+=str(node.val)# 叶子结点if not node.left and not node.right:paths.append(path)else:path+="->"find_path(node.left,path)find_path(node.right,path)paths = []find_path(root,"")return paths

image-20231114160516588

使用BFS解决

class Solution:def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:# 使用BFS 层次遍历paths = []if not root:return pathsqueue = [root]path_lst = [str(root.val)]while queue:node = queue.pop(0)path = path_lst.pop(0)if not node.left and not node.right:paths.append(path)else:if node.left:queue.append(node.left)path_lst.append(path+"->"+str(node.left.val))if node.right:queue.append(node.right)path_lst.append(path+"->"+str(node.right.val))return paths

image-20231114162537557

113、路径总和II

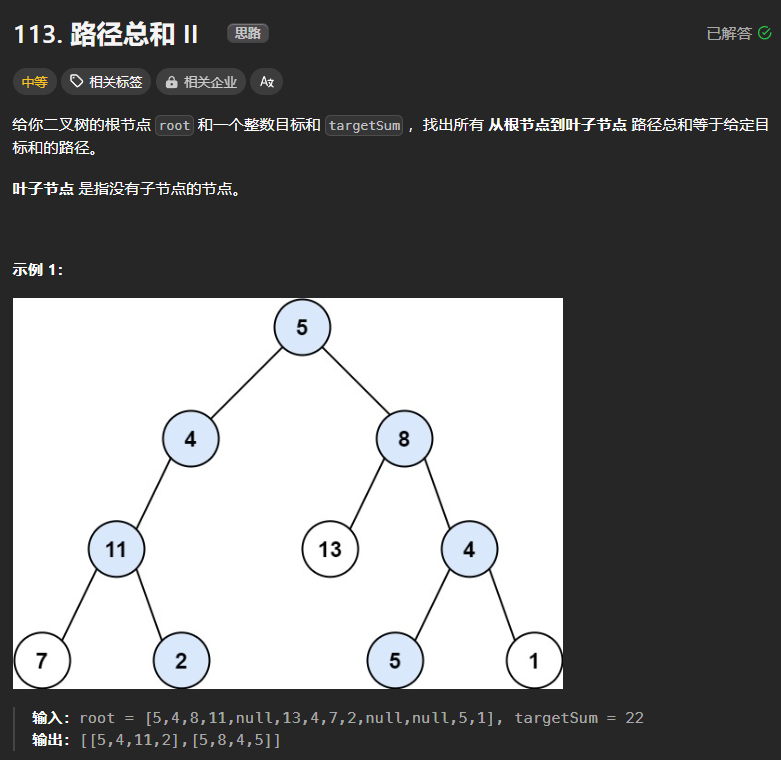
image-20231114160701463

class Solution:def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:def find_path(node,path):if node:# path+=[node.val]path=path+[node.val]if not node.left and not node.right:if sum(path)==targetSum:paths.append(path)else:find_path(node.left,path)find_path(node.right,path)paths = []find_path(root,[])return paths

image-20231114161838454

这里需要注意一个问题，就是path+=[node.val]和path=path+[node.val]这两句代码的写法有点不同，+=是在原来的path上进行修改，而直接赋值是可以形成一个新的列表，在递归的过程中就出现一个新的列表。这是由于python中列表是可变类型的，如果列表也是和字符串一样属于不可变类型的话，就可以直接使用+=操作了。

988、从叶结点开始的最小字符串

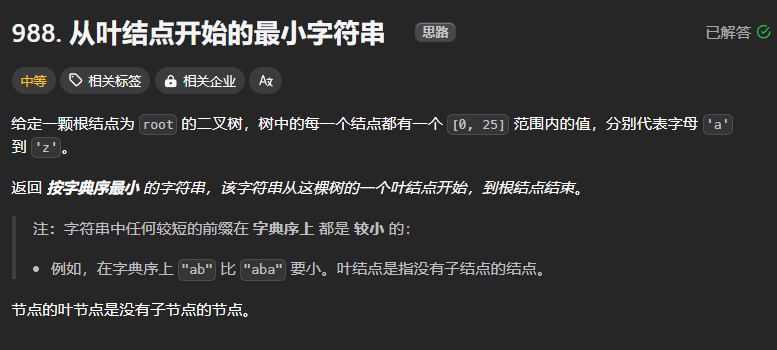
image-20231114170051688

image-20231114170117467

本题思路与二叉树的所有路径思路一致，只需要在其中添加一个用来进行比较的变量即可，注意这里所说的变量不可以是字符串，因为字符串是不可修改的。这里也需要注意是从叶子结点开始的，所以最终求得的路径path需要进行逆序处理[::-1]

class Solution:def smallestFromLeaf(self, root: Optional[TreeNode]) -> str:# print(myhash)def find_path(node,path):if node:path+=str(myhash[node.val])# print(node.val,path)if not node.left and not node.right:minleaf[0] = min(minleaf[0],path[::-1])else:find_path(node.left,path)find_path(node.right,path)myhash = {i: chr(ord('a') + i) for i in range(26)}minleaf = ["z"*8500]find_path(root,"")return minleaf[0]

image-20231114170241494

404、左叶子之和

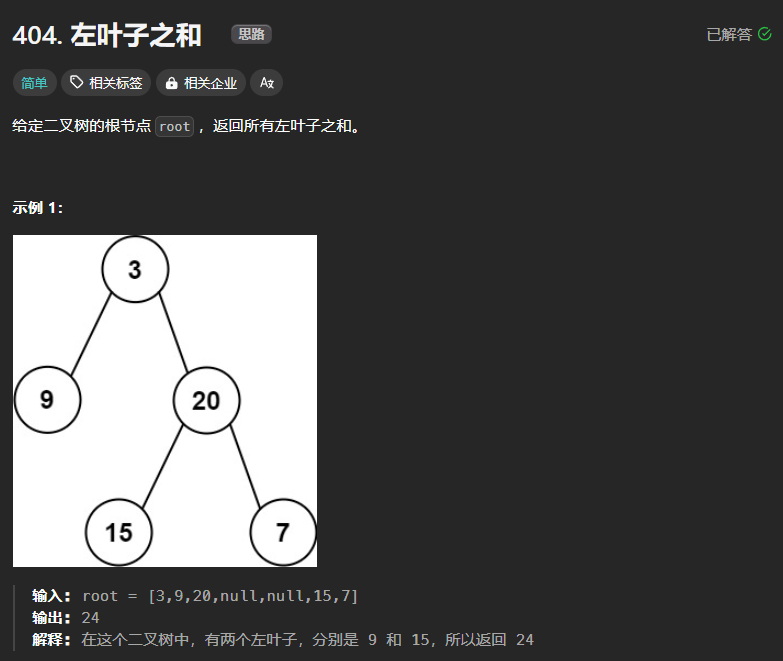
image-20231114204344749

思路：

本题采用DFS的方式去解决。需要注意到底什么是左叶子，左叶子是指该节点不为空，同时其左右孩子为空，通过递归的方式去寻找这样的结点，然后对其求和。

class Solution:def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:# 递归程序如果碰到结点为空则返回0if not root:return 0# 如果该节点没有左右孩子 也返回if not root.left and not root.right:return 0# 遍历左子树left_num = self.sumOfLeftLeaves(root.left)# 如果有左孩子并且孩子为叶子结点则进行统计if root.left and not root.left.left and not root.left.right:left_num = root.left.valright_num = self.sumOfLeftLeaves(root.right)return left_num + right_num

image-20231116171305355

236、二叉树的最近公共祖先

image-20231116171451621

从下往上对结点进行处理，采用后序遍历的方法，先左再右再中

情况1： p和q都为某个节点的孩子结点

情况2：p是q的父节点或者q是p的父节点

class Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':if not root:return rootif root==q or root==p:return rootleft = self.lowestCommonAncestor(root.left,p,q)right = self.lowestCommonAncestor(root.right,p,q)if left and right:return rootelif not left and right:return rightelif not right and left:return leftelif not left and not right:return left

106、从中序和后序遍历序列构造二叉树

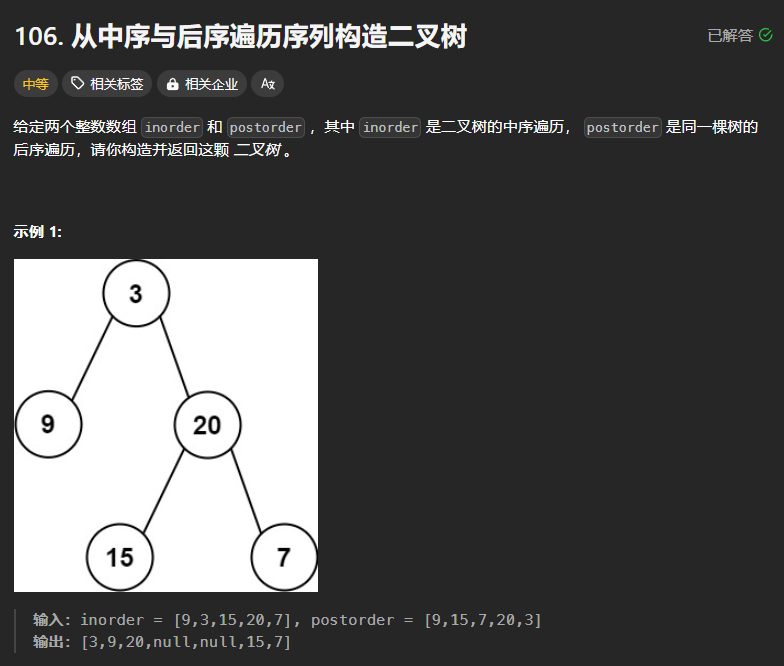
image-20231117165833569

思路：

首先在后序遍历序列中找到根结点，然后创建一个根节点

找到切割的位置

  • 对先序序列进行切割，分为左子树和右子树

  • 对后序序列进行切割，分为左子树和右子树

  • 构造根节点的左子树，使用递归的方法，传递进去的参数是先序数组的左边和中序数组的左边

  • 构造根节点的右子树，使用递归的方法，传递进去的参数是先序数组的右边和中序数组的右边

class Solution:def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:if not postorder:return None# 找到根结点root_val = postorder[-1]root = TreeNode(root_val)# 找到切割位置qiege = inorder.index(root_val)inorder_left = inorder[:qiege]inorder_right = inorder[qiege+1:]postorder_left = postorder[:len(inorder_left)]postorder_right = postorder[len(inorder_left):len(postorder)-1]root.left = self.buildTree(inorder_left,postorder_left)root.right = self.buildTree(inorder_right,postorder_right)return root

105、从先序遍历与中序遍历构造二叉树

需要注意的是：在寻找先序遍历进行迭代的时候，由于根节点是一定位于第一位的，所以寻找左和右的时候切割点是从位置1开始（包含位置1）往后找len(inorder_left)这个大小，然后剩余的部分【preorder[1+len(inorder_left)]】作为preorder_right

class Solution:def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:# 通过数组来构造二叉树if not preorder:return Noneroot_val = preorder[0]root = TreeNode(root_val)qiege = inorder.index(root_val) # 中序切割点# print(qiege,inorder)/inorder_left = inorder[:qiege] # 中序inorder_right = inorder[qiege+1:]preorder_left = preorder[1:1+len(inorder_left)]preorder_right = preorder[1+len(inorder_left):]root.left = self.buildTree(preorder_left,inorder_left)root.right = self.buildTree(preorder_right,inorder_right)return root

654、最大二叉树

image-20231117192616419

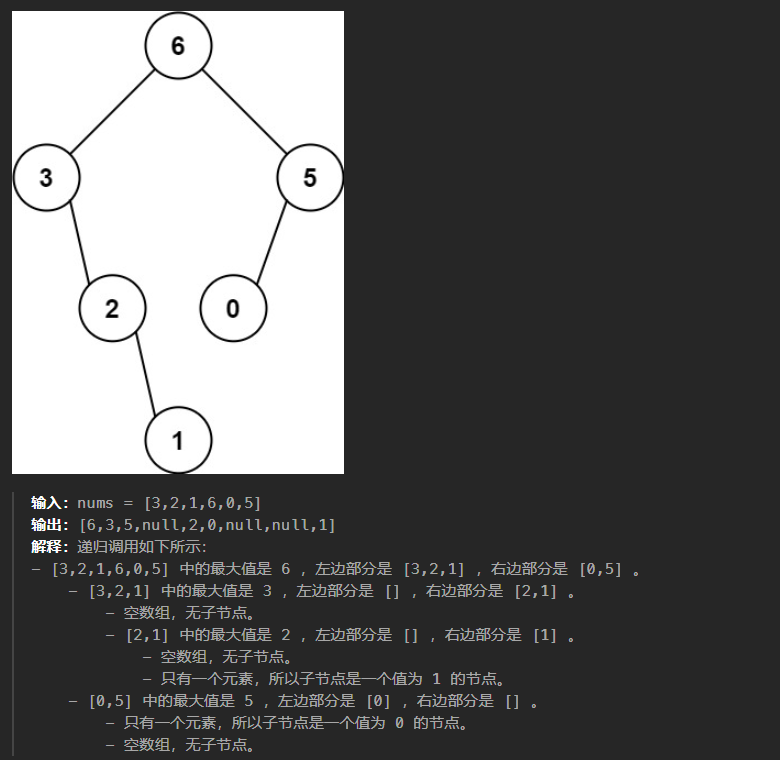
image-20231117192638755

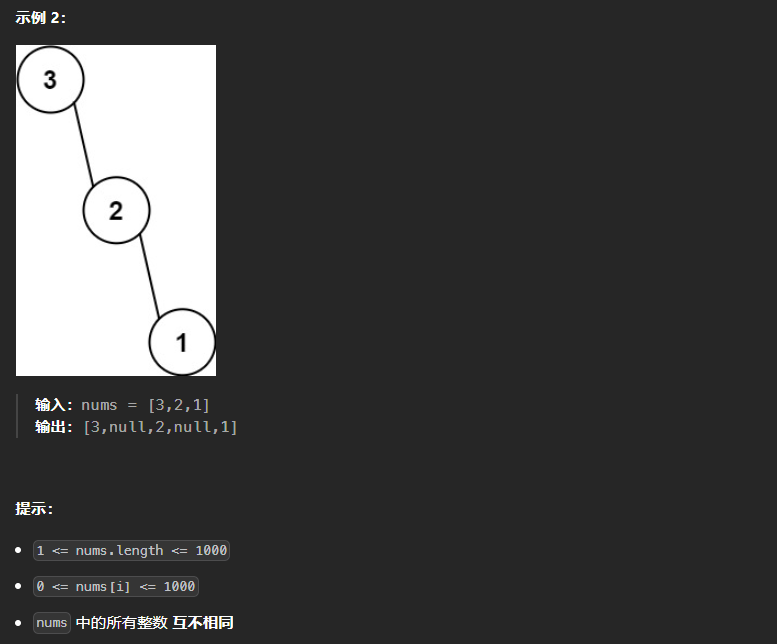
image-20231211191504330

思路：使用递归的方式

递归三部曲

  • 递归函数的参数和返回值

返回值为TreeNode类型

参数为nums数组

  • 终止条件

题目中的范围nums的长度是大于等于1的，因此不需要考虑nums为空的情况

  • 单层递归逻辑

  1. 找到数组中最大值的下标，最大值用来构造根节点，下标用来对数组进行切割

    maxValue = float("-inf")
maxIndex = 0
for i,value in enumerate(nums):if maxValue<value:maxValue = valuemaxIndex = i

  2. 最大值左区间 构造左子树

    if maxIndex > 0:new_list = nums[:maxIndex]node.left = self.

  3. 最大值右区间 构造右子树

首先根据最大值对该数组进行切割，切割完毕后，根据数组的左边与右边分别进行递归，这类似于106从中序和后序遍历序列构造二叉树。最终返回构造好的二叉树root。

class Solution:def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:if not nums:return Noneif len(nums)==1:return TreeNode(nums[0])root_val = max(nums)root = TreeNode(root_val)qiege = nums.index(root_val)nums_left = nums[:qiege]nums_right = nums[qiege+1:]root.left = self.constructMaximumBinaryTree(nums_left)root.right = self.constructMaximumBinaryTree(nums_right)return root

image-20231117192833812

998、最大二叉树II

image-20231117192902002

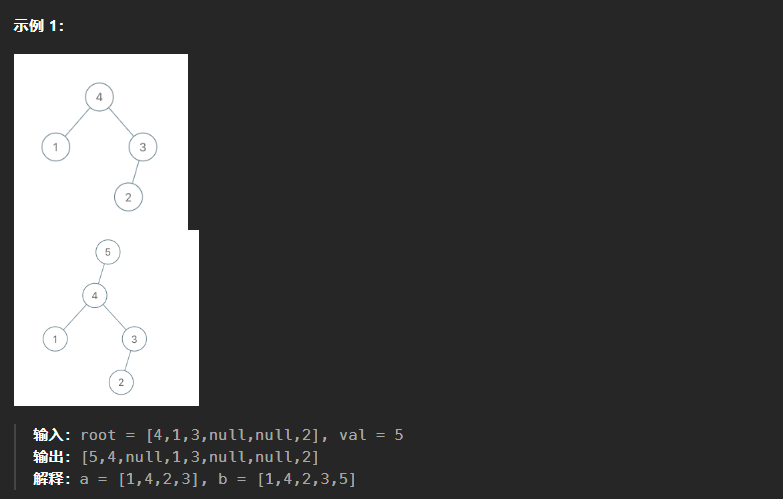
image-20231117192919398

image-20231117192933861

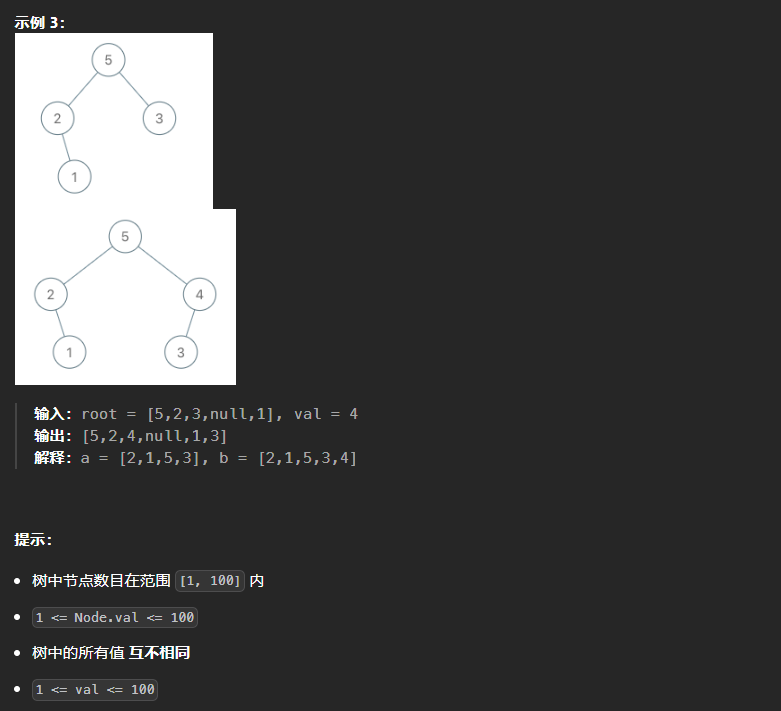
image-20231117192954360

本题和上一题相比，难点就在于可能需要对这颗二叉树进行重新构造，但是在构造的过程中也有省事的地方，就是只需要往右插入。如果val值大于原树的根节点值，则直接将原树放在val结点的左子树即可。如果小于最大值，向右子树进行遍历，同时记录当前结点的父节点，方便val结点的插入。

class Solution:def insertIntoMaxTree(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:node = TreeNode(val)prev = Nonecur = root# 遍历root 往右子树遍历while cur and cur.val>val:# 记录当前结点的父节点prev = curcur = cur.right# 如果val大于原树的最大值if not prev:node.left = curreturn node# 遍历到了右子树合适的位置 换结点else:# prev.right = nodenode.left = curreturn root

98、验证二叉搜索树（二叉排序树BST）

image-20231117220106841

本题思路很简单，利用二叉排序树的性质即可：二叉排序树中序遍历的结果是递增的。

方法：

  • 采用非递归遍历算法 设置最小值 在中序递归的过程中进行比较
  • 采用迭代法，设置最小值，如果出现不满足性质的节点直接返回False
# 递归遍历算法
class Solution:# 添加一个最小值 每次进行比较的时候更新最小值def __init__(self):self.min_= float("-inf")def isValidBST(self, root: Optional[TreeNode]) -> bool:if not root:return True# 左left = self.isValidBST(root.left)# 根if self.min_ < root.val:self.min_ = root.valelse:return False# 右right = self.isValidBST(root.right)return left and right

image-20231117220442215

# 非递归遍历算法
class Solution:def isValidBST(self, root: Optional[TreeNode]) -> bool:# 中序遍历 判断值是否小于等于if not root:return Truestack = []p = rootmin_ = float("-inf")while p or stack:if p:stack.append(p)p = p.leftelse:p = stack.pop()# print(min_,p.val)if min_ < p.val:min_ = p.valelse:return Falsep = p.rightreturn True

image-20231117220417506

501、二叉搜索树中的众数

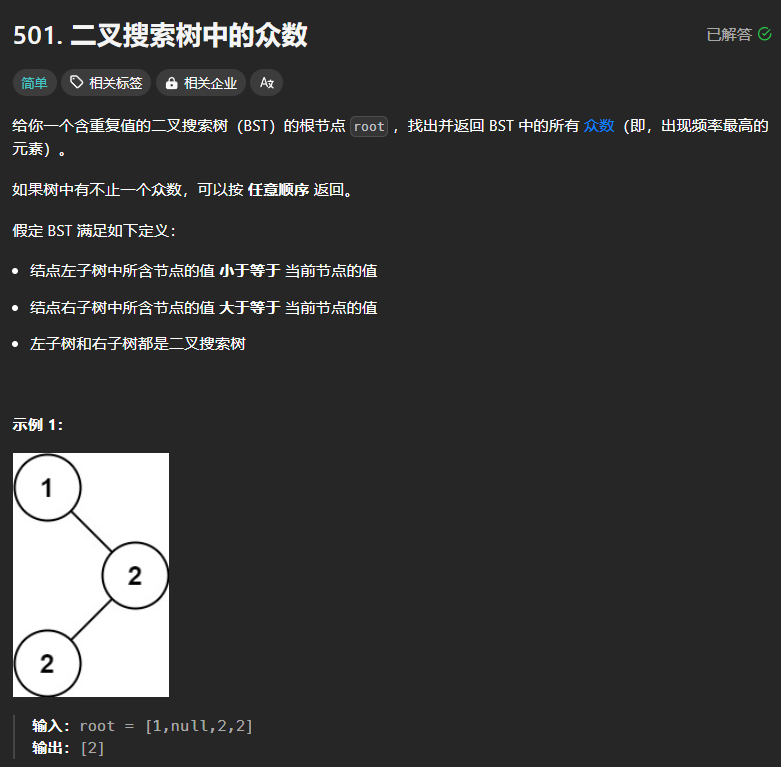
image-20231118203749353

思路：

对二叉树进行中序遍历，遍历的过程中统计字符出现的最大次数。其中在递归的过程中需要将max_freq指定为全局变量。

class Solution:def findMode(self, root: Optional[TreeNode]) -> List[int]:max_freq = 0myhash = {}def dfs(root):nonlocal max_freqif not root:return dfs(root.left)myhash[root.val] = myhash.get(root.val,0)+1max_freq = max(max_freq, myhash[root.val])dfs(root.right)dfs(root)return [k for k,v in myhash.items() if v==max_freq]

结果

image-20231118203735546

  • 使用迭代法的中序遍历同时不使用字典来统计出现的频率
class Solution:def findMode(self, root: Optional[TreeNode]) -> List[int]:# 使用迭代法的中序遍历stack = []p = rootpre = Nonefreq = 0max_freq = 0res = []while stack or p:if p:stack.append(p)p = p.leftelse:p = stack.pop()if pre is None:freq = 1elif pre.val == p.val:freq+=1else:freq = 1# 如果频率和最大频率相等 则往结果数组中添加if freq==max_freq:res.append(p.val)if freq > max_freq:res = [p.val]max_freq = freqpre = pp = p.rightreturn res

这个方法的核心是用freq和max_freq进行比较，同时使用pre指针指向前一个结点，这样就方便在中旬遍历的过程中记录已经出现的结点值了。有如下几种情况：

  • 针对pre
    • 如果pre为None，则更新freq=1
    • 如果pre不为None且pre的值与p的值相等，则将freq+1
    • 如果pre不为None且pre的值与``p不相等，仍然将freq`=1
  • 针对freq和max_freq
    • 如果freq==max_freq，则往返回值的列表中添加该元素（p.val 即结果的众数）
    • 如果freq>max_freq，则对res列表进行更新，同时更新max_freq
    • 如果freq<max_freq，可以不进行任何处理

701、二叉搜索树中的插入

image-20231120105950581

遍历二叉树直到该值应该出现的地方为止，利用二叉搜索树的性质，如果根节点的值小于value，则再右子树进行递归，否则在左子树进行递归。

class Solution:def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:# 根if not root:return TreeNode(val)if root.val>val:root.left = self.insertIntoBST(root.left,val)if root.val < val:root.right = self.insertIntoBST(root.right,val)return root

image-20231120110120885

450、二叉搜索树中的删除

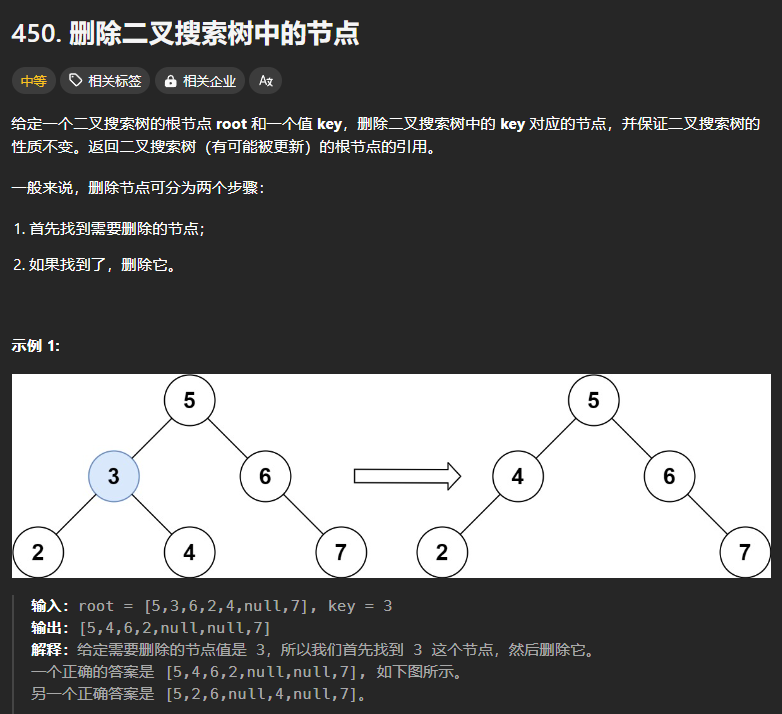
image-20231120104451186

题目中要求的返回值是二叉搜索树中可能被更新的根结点的引用

class Solution:def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:if not root:return rootif root.val==key:if not root.right and not root.left:return Noneelif not root.left:return root.rightelif not root.right:return root.leftelse:cur = root.rightwhile cur.left is not None:cur = cur.leftcur.left = root.leftreturn root.rightelif root.val > key:root.left =  self.deleteNode(root.left,key)else:root.right = self.deleteNode(root.right,key)return root

image-20231120105811069

108、将有序数组转化为二叉搜索树

image-20231121102406870

思路：本题思路类似于从106、中序和后序遍历构序列构造二叉树和654、最大二叉树的解题思路，需要找到中间的切割点，然后通过递归的方式分别构造左右子树，需要注意的就是对于递归的结束条件的处理如下：

if not nums:return None
if len(nums)==1:return TreeNode(nums[0])

一共两种情况，因为再往下就涉及到数组的切割问题。

  • 如果数组为空，则直接返回None
  • 如果数组的长度为1，则直接返回以数组中唯一元素构造出二叉树结点即可
class Solution:def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:# 本题思路就是通过数组来构造一颗二叉树，需要保持树的平衡，方法将就是从中间进行构造if not nums:return Noneif len(nums)==1:return TreeNode(nums[0])qiege = len(nums)//2# print(qiege)root = TreeNode(nums[qiege])nums_left = nums[:qiege]nums_right = nums[qiege+1:]root.left = self.sortedArrayToBST(nums_left)root.right = self.sortedArrayToBST(nums_right)return root

image-20231121103147381

123、有序链表转换为二叉搜索树

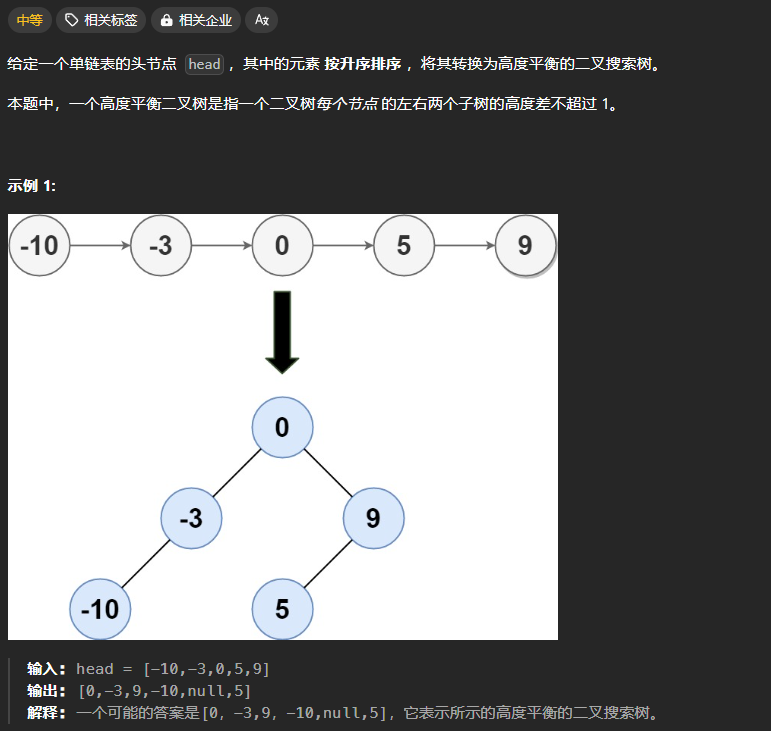
image-20231223184702366

本题中的要求是转换为高度平衡的二叉搜索树，即要求是一颗平衡二叉树，所以需要从数组的中间进行构建，核心思路参考108题。

class Solution:def sortedListToBST(self, head: Optional[ListNode]) -> Optional[TreeNode]:# 如何构建二叉搜索树？def construct(nums):if not nums:return Noneif len(nums)==1:return TreeNode(nums[0])qiege = len(nums)//2root = TreeNode(nums[qiege])nums_left = nums[:qiege]nums_right = nums[qiege+1:]root.left = construct(nums_left)root.right = construct(nums_right)return rootp = headnums = []while p:nums.append(p.val)p=p.nextnums.sort()return construct(nums)

image-20231223185524344

538、把二叉搜索树转换为累加树

image-20231121143208244

针对二叉搜索树的题目，一定要好好利用其中序遍历得到的是一个递增的序列这一性质！！！

思路：根据题目的要求，本题中的树是二叉搜索树，在中序遍历的过程中是递增的，但是要求实现的是将node节点的的值修改为大于等于该节点值的所有节点值的和。因此我们可以采用逆序中序遍历的方法，逆序中序遍历中的结点值与当前结点的结点值相加起来，得到该结点现在的值。

需要注意的是，使用Python的时候，局部变量的问题，也就是我们pre指向前一个结点值，我们需要用nonlocal pre来申明pre不是局部变量，这样在递归的过程中才能够访问到外层嵌套函数中定义的pre值。

class Solution:def bstToGst(self, root: TreeNode) -> TreeNode:# 使用右中左的遍历顺序进行遍历 往前叠加值def dfs(root):nonlocal preif not root:return dfs(root.right)root.val += prepre = root.valdfs(root.left)pre = 0dfs(root)return root

image-20231121143137935

1038、从二叉搜索树到更大的和树

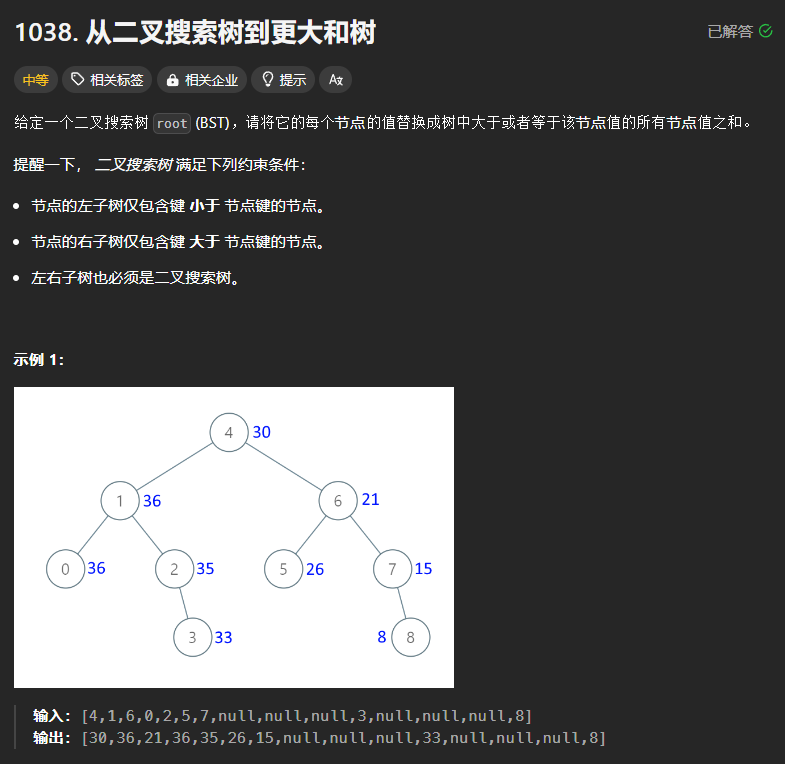
image-20231121142641537

本题与上一题思路一样，不再重复赘述。

530、二叉树的最小绝对值差

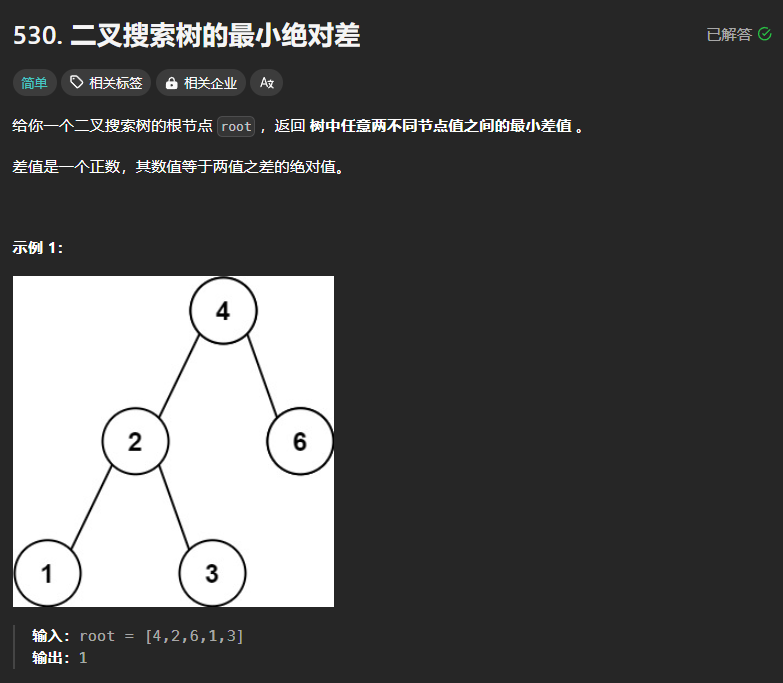
image-20231121143459700

思路：本题的树是二叉搜索树，根据其性质可以进行中序遍历，然后在得到的遍历序列中求最小绝对差

方法1 递归方法

class Solution:def getMinimumDifference(self, root: Optional[TreeNode]) -> int:def dfs(root):if not root:return []return dfs(root.left) + [root.val] + dfs(root.right)nums = dfs(root)res = float("inf")for i in range(len(nums)-1):res = min(abs(nums[i]-nums[i+1]),res)return res

方法2 迭代方法

在迭代法中，需要用pre记录前一个节点的指针，其初始值可以设置为任意值

class Solution:def getMinimumDifference(self, root: Optional[TreeNode]) -> int:# 使用中序遍历 然后求差值stack = []p = rootpre = float("inf")res = float("inf")while p or stack:if p:stack.append(p)p = p.leftelse:p = stack.pop()res = min(abs(pre-p.val),res)pre = p.valp = p.rightreturn res

image-20231121150414365

99、恢复二叉搜索树

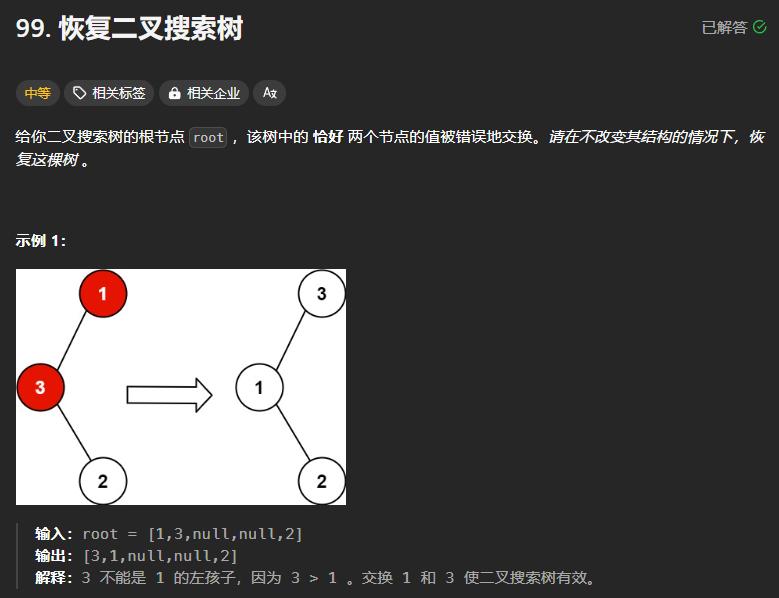
image-20231223101258925

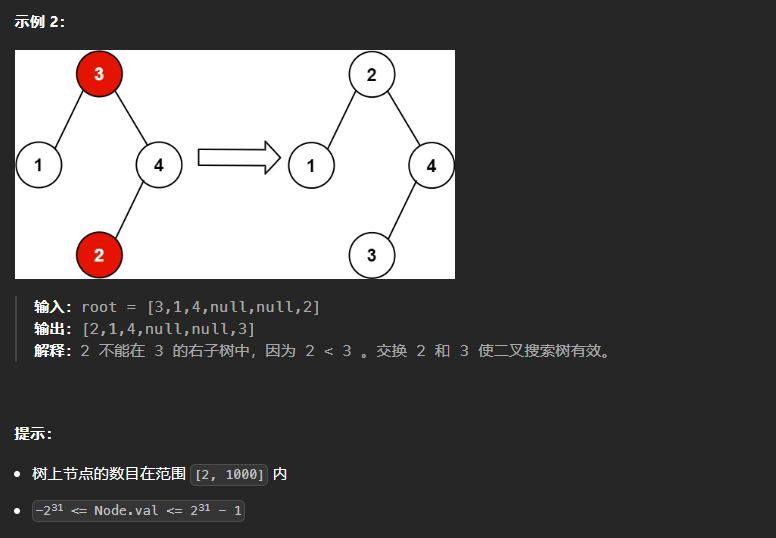
image-20231223101317451

本题的思路是：寻找出两个顺序颠倒的两个位置，在树遍历结束之后交换两个的值

bigger和smaller分别记录最大和最小值，其中bigger在进行初始化的时候需要进行赋值

bigger = TreeNode(float("-inf"))

class Solution:def recoverTree(self, root: Optional[TreeNode]) -> None:"""Do not return anything, modify root in-place instead."""# 中序遍历 交换节点stack = []p = rootpre = Nonesmaller = Nonebigger = TreeNode(float("-inf"))while p or stack:if p:stack.append(p)p = p.leftelse:p = stack.pop()# print(p.val,end=" ")if pre and pre.val>p.val:if bigger.val < pre.val:bigger = presmaller = ppre = pp = p.rightsmaller.val,bigger.val = bigger.val,smaller.val

image-20231223102107530

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/812101.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

蓝桥杯-STL-string

蓝桥杯-STL-string

目录 字符串定义 字符串初始化 字符串输入输出 字符串输出 字符串输入 字符串访问 字符串拷贝 字符串拼接 直接相加 append(const char*str,int n) 字符串比较 ​编辑字符串长度length()/size() 字符串查找find(string str) 查找子串substr(int a,int b) 字符串的…
阅读更多...
秋招数据库学习2（20240408-20240412共10道）

秋招数据库学习2（20240408-20240412共10道）

由于感觉数据库难度可能暂时面试用不到&#xff0c;就先不刷啦 20240408 1.从不订购的客户 SELECT Name AS Customers FROM Customers C LEFT JOIN Orders O ON C.Id O.CustomerId WHERE CustomerId is nullselect customers.name as Customers from Customers wher…
阅读更多...
手写ArrrayList

手写ArrrayList

需求 自定义的MyArrayList import java.util.Arrays; import java.util.Objects;public class MyArrayList<E> {private Object[] elementData ; // 存储元素的数组private int size; // 记录 的元素个数private static final int DEFAULT_CAPACITY 10; // 默认容量// …
阅读更多...
Eigen笔记2：矩阵拼接

Eigen笔记2：矩阵拼接

直接贴代码吧&#xff0c;使用的MatrixXd 和<<运算符&#xff1a; int main(int argc, char *argv[]) {Eigen::MatrixXd B(2, 2);B << 1, 2,3, 4;Eigen::MatrixXd C(2, 2);C << 5, 6,7, 8;Eigen::MatrixXd D(2, 2);D << 9, 10,11, 12;Eigen::MatrixXd…
阅读更多...
基于React封装Handsontable并兼容antd

基于React封装Handsontable并兼容antd

背景 其实Handsontable官方也提供了React的版本&#xff0c;但是官方的版本再编辑和渲染的时候并不能够很好的嵌入第三方的组件库。这就导致了&#xff0c;使用了Handsontable就没有办和普通的react项目一样轻松引用其他第三方组件。因此对其react的版本进行了二次的封装&#…
阅读更多...
Django中间件路由映射自动加/斜杠问题原因及分析

Django中间件路由映射自动加/斜杠问题原因及分析

输入 http://127.0.0.1:8000/main/index/ 输入 http://127.0.0.1:8000/main/index 路由定义情况 urlpatterns [path("index/", views.index) ]可以发现我在输入URL的index路由时&#xff0c;如果没有和Django定义的路由匹配规则一样的话&#xff0c;浏览器自…
阅读更多...
Vim：强大的文本编辑器

Vim：强大的文本编辑器

文章目录 Vim&#xff1a;强大的文本编辑器Vim的模式命令模式常用操作光标移动文本编辑查找和替换 底行命令模式常用操作Vim的多窗口操作批量注释与去注释Vim插件推荐&#xff1a;vimforcpp结论 Vim&#xff1a;强大的文本编辑器 Vim&#xff0c;代表 Vi IMproved&#xff0c;…
阅读更多...
如何确保软件通过SmartScreen验证，消除用户下载时的警告提示？

如何确保软件通过SmartScreen验证，消除用户下载时的警告提示？

在当前的网络时代&#xff0c;各种软件应用程序深深渗透到人们的日常生活和工作中&#xff0c;许多企业选择自行开发应用程序以推进其业务发展。但在发布应用程序后&#xff0c;软件所有者经常会遇到一个挑战&#xff0c;即用户在下载时可能会遇到微软SmartScreen提示“此应用程…
阅读更多...
探索HTTP协议的世界 | 从基础到高级应用，原理与实践相结合（请求篇）

探索HTTP协议的世界 | 从基础到高级应用，原理与实践相结合（请求篇）

从基础到高级应用&#xff0c;原理与实践相结合 什么是Http历代Http协议主要特点格式和URL协议内容请求行格式如下请求方法简单案例 消息报头报头域的格式HTTP消息报头类型普通报头优化方向报头&#xff08;缓存&#xff09;Cache-Control的选项其他相关的缓存报头 请求报头Acc…
阅读更多...
Unity TMP Inputfield 输入框 框选 富文本 获取真实定位

Unity TMP Inputfield 输入框 框选 富文本 获取真实定位

一、带富文本标签的框选是什么 UGUI的InputField提供了selectionAnchorPosition和selectionFocusPosition&#xff0c;开始选择时的光标下标和当前光标下标 对于未添加富文本标签时&#xff0c;直接通过以上两个值&#xff0c;判断一下框选方向&#xff08;前向后/后向前&…
阅读更多...
C#Winform使用扩展方法自定义富文本框(RichTextBox)字体颜色

C#Winform使用扩展方法自定义富文本框(RichTextBox)字体颜色

实现效果 调用方法 rtxtLog.AppendTextColorful(richTextBox1,DateTime.Now.ToString(), Color.Red); 完整代码如下 using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using Sys…
阅读更多...
【U8+】用友固定资产卡片拆分提示：未设置对象变量或With block变量。

【U8+】用友固定资产卡片拆分提示：未设置对象变量或With block变量。

【问题描述】 用友U8软件中&#xff0c; 操作固定资产模块&#xff0c;针对资产进行卡片拆分的时候&#xff0c; 提示&#xff1a;未设置对象变量或With block变量。 确定后仍然能打开卡片拆分界面&#xff0c;但是界面显示异常看不到拆分明细信息&#xff0c;并且保存后拆分结…
阅读更多...
【Qt-Qt Creator使用技巧】

【Qt-Qt Creator使用技巧】

工具-Qt Creator ■ 使用技巧■ 定义触发片段■ Qt Creator 行编辑■ 代码注释■ 代码补全■ 快速给函数添加定义■ 创建书签■ 同步列输入■ 局部替换■ 源代码阅读■ 源码调试■ 使用技巧 ■ 定义触发片段 ■ Qt Creator 行编辑 shift + alt + up / down来获得多个游标。 …
阅读更多...
导入芯片原厂SDK Mirror源码到gerrit

导入芯片原厂SDK Mirror源码到gerrit

下载镜像代码 repo init --mirror --repo-url ssh://xx/repo.git -u ssh://xx/manifests.git -m manifest.xml repo sync 创建AOSP project 对All Project权限修改 创建repo 在刚才下载的codebase根目录执行如下命令&#xff1a; repo forall -c echo $REPO_PROJECT; ssh -p 29…
阅读更多...
DOTS Instancing合批:如何针对单个渲染实体修改材质参数

DOTS Instancing合批:如何针对单个渲染实体修改材质参数

最近在做DOTS的教程,由于DOTS(版本1.0.16)目前不支持角色的骨骼动画&#xff0c;我们是将角色的所有动画数据Baker到一个纹理里面&#xff0c;通过修改材质中的参数AnimBegin,AnimEnd来决定动画播放的起点和终点&#xff0c;材质参数AnimTime记录当前过去的动画时间。但是在做大…
阅读更多...
CSS导读 （元素显示模式 下）

CSS导读 （元素显示模式 下）

&#xff08;大家好&#xff0c;今天我们将继续来学习CSS的相关知识&#xff0c;大家可以在评论区进行互动答疑哦~加油&#xff01;&#x1f495;&#xff09; 目录 3.6 元素显示模式转换 3.7 (一个小技巧)单行文字垂直居中的代码 3.8 单行文字垂直居中的原理 3.9 小案例…
阅读更多...
leaflet知识点：地图窗格panes的应用

leaflet知识点：地图窗格panes的应用

一&#xff0c;需求背景 地图中存在无人机&#xff0c;停机坪&#xff0c;航线三个图层&#xff0c;需要实现无人机图层显示在最上面&#xff0c;停机坪图层显示在最下面&#xff0c;航线图层显示在中间。 二&#xff0c;遇到问题 由下图可知航线图层所在overlayPane窗格的z-…
阅读更多...
工控 modbusTCP 报文

工控 modbusTCP 报文

Tx 发送报文:00 C9 00 00 00 06 01 03 00 00 00 02 Rx 接收报文:00 C9 00 00 00 07 01 03 04 01 4D 00 01 Tx 发送报文:00 C9 00 00 00 06 01 03 00 00 00 02 00 C9 事务处理标识符 2字节 00 00 协议标识符 2字节 固定 00 00 00 06 长度 2字节 表示之后的字节总数 &#xff08;…
阅读更多...
大数据之ClickHouse

大数据之ClickHouse

大数据之ClickHouse 简介 ClickHouse是一种列式数据库管理系统&#xff0c;专门用于高性能数据分析和数据仓库应用。它是一个开源的数据库系统&#xff0c;最初由俄罗斯搜索引擎公司Yandex开发&#xff0c;用于满足大规模数据分析和报告的需求。 特点 开源的列式存储数据库…
阅读更多...
elementUI 下拉框加提示文案

elementUI 下拉框加提示文案

效果如下&#xff1a; 展示文案在最下面&#xff0c;跟选项有个分割线 <el-select v-model"value" placeholder"请选择" clearable popper-class"addNotice" class"addNoticeS" visible-change"(v) >selectNotice(v,展示…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023