- 掌握单位根检验的原理并能解读结果;
- 掌握利用序列的自相关图和偏自相关图识别模型并进行初步定阶。
原始数据在文末!!!
练习1、根据某1971年9月-1993年6月澳大利亚季度常住人口变动(单位:千人)的数据(行数据)(题目1数据.txt),求:
(1)通过时序图、样本自相关图、单位根检验,判断该序列的平稳性;
(2)判断该序列的纯随机性;
(3)如果序列平稳且非白噪声,绘制样本自相关图(ACF)和偏自相关图(PACF),根据相关性特征,选择适当模型拟合该序列的发展。
data1 <- scan("F:/时间序列分析/实验5/习题数据/题目1数据.txt")
x1 <- ts(data1,start = c(1971,3),frequency = 4)
plot(x1)#时序图
acf(x1)#自相关图
install.packages("aTSA")
library(aTSA)
adf.test(x1)#单位根检验for(i in 1:2)print(Box.test(x1,type = "Ljung-Box",lag = 6*1))#白噪声检验
pacf(x1)#偏自相关图
结果分析:
- 时序图:
该序列始终在常数50附近波动,且波动范围有界。无明显的趋势性或周期性。该序列是平稳序列。

自相关图:
显示除了lag=0.75和lag=2的自相关系数在2倍标准差范围之外,其他阶数的自相关系数都在2倍标准差范围内波动。可以判断该序列具有短期相关性,进一步确定序列平稳。

单位根检验:
检验结果显示该序列可认为是平稳序列(带漂移项1-2阶滞后模型和既有漂移项又有趋势项的1-2阶滞后模型的P值小于0.05)。
adf.test(x1)
Augmented Dickey-Fuller Test
alternative: stationary
Type 1: no drift no trend
lag ADF p.value
[1,] 0 -2.719 0.010
[2,] 1 -1.531 0.128
[3,] 2 -0.928 0.345
[4,] 3 -0.698 0.428
Type 2: with drift no trend
lag ADF p.value
[1,] 0 -10.12 0.010
[2,] 1 -6.41 0.010
[3,] 2 -3.56 0.010
[4,] 3 -2.32 0.207
Type 3: with drift and trend
lag ADF p.value
[1,] 0 -10.48 0.0100
[2,] 1 -6.88 0.0100
[3,] 2 -3.92 0.0172
[4,] 3 -2.57 0.3362
----
Note: in fact, p.value = 0.01 means p.value <= 0.01
2.白噪声检验:
延迟6阶和延迟12阶的LB统计量的P值为都小于α=0.05,则拒绝原假设,认为序列不是白噪声序列。
Box-Ljung test
data: x1
X-squared = 17.858, df = 6, p-value = 0.006597
Box-Ljung test
data: x1
X-squared = 17.858, df = 6, p-value = 0.006597
3.偏自相关图:
除了lag=0.75,lag=1,lag=1.75偏自相关系数非常显著地≠0,之后其他阶数的偏自相关系数都迅速地向0值靠拢。

练习2、根据某城市过去四年每个月人口净流入数量(行数据)(题目2数据.txt),求:
(1)通过时序图、样本自相关图、单位根检验,判断该序列的平稳性;
(2)判断该序列的纯随机性;
(3)如果序列平稳且非白噪声,绘制样本自相关图(ACF)和偏自相关图(PACF),根据相关性特征,选择适当模型拟合该序列的发展。
Data2 <- scan("F:/时间序列分析/实验5/习题数据/题目2数据.txt")
x2 <- ts(data2,start = c(2018,1),frequency = 12)
plot(x2)#时序图
acf(x2)#自相关图library(aTSA)
adf.test(x2)#单位根检验for(i in 1:2)print(Box.test(x2,type = "Ljung-Box",lag = 6*1))#白噪声检验
pacf(x2)#偏自相关图
结果分析:
- 时序图:
该序列始终在常数4附近波动,且波动范围有界。无明显的趋势性或周期性。该序列是平稳序列。

自相关图:
显示除了lag=1/12的自相关系数在2倍标准差范围之外,其他阶数的自相关系数都在2倍标准差范围内波动。可以判断该序列具有短期相关性,进一步确定序列平稳。

单位根检验:
检验结果显示该序列可认为是平稳序列(带漂移项1-2阶滞后模型和既有漂移项又有趋势项的1-3阶滞后模型的P值小于0.05)。
Augmented Dickey-Fuller Test
alternative: stationary
Type 1: no drift no trend
lag ADF p.value
[1,] 0 -1.121 0.274
[2,] 1 -0.960 0.331
[3,] 2 -0.731 0.413
[4,] 3 -0.986 0.322
Type 2: with drift no trend
lag ADF p.value
[1,] 0 -4.03 0.0100
[2,] 1 -4.49 0.0100
[3,] 2 -3.11 0.0356
[4,] 3 -2.93 0.0503
Type 3: with drift and trend
lag ADF p.value
[1,] 0 -4.54 0.0100
[2,] 1 -5.74 0.0100
[3,] 2 -4.33 0.0100
[4,] 3 -3.81 0.0255
----
Note: in fact, p.value = 0.01 means p.value <= 0.01
2.白噪声检验:
延迟6阶和延迟12阶的LB统计量的P值为都大于α=0.05,则接受原假设,认为序列是白噪声序列。
Box-Ljung test
data: x2
X-squared = 11.938, df = 6, p-value = 0.06336
Box-Ljung test
data: x2
X-squared = 11.938, df = 6, p-value = 0.06336
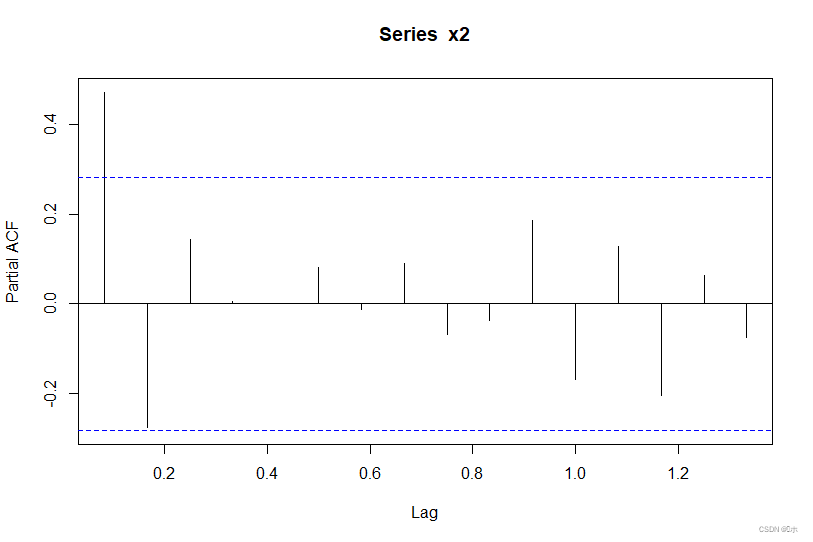
3.偏自相关图:
除了1/12阶偏自相关系数非常显著地≠0,之后其他阶数的偏自相关系数都迅速地向0值靠拢,序列平稳。
练习3、根据1975-1980年夏威夷岛莫那罗亚火山每月释放的CO2数据(题目3数据.txt),求:
(1)通过时序图、样本自相关图、单位根检验,判断该序列的平稳性;
(2)判断该序列的纯随机性;
(3)如果序列平稳且非白噪声,绘制样本自相关图(ACF)和偏自相关图(PACF),根据相关性特征,选择适当模型拟合该序列的发展。
data3 <- scan("F:/时间序列分析/实验5/习题数据/题目3数据.txt")
x3 <- ts(data3,start = c(1975,1),frequency = 12)
plot(x3)#时序图
acf(x3)#自相关图library(aTSA)
adf.test(x3)#单位根检验for(i in 1:2)print(Box.test(x3,type = "Ljung-Box",lag = 6*1))#白噪声检验
pacf(x3)
结果分析:
- 时序图:
该序列呈现出逐年的上升趋势且存在明显的周期性。该序列不是平稳序列。

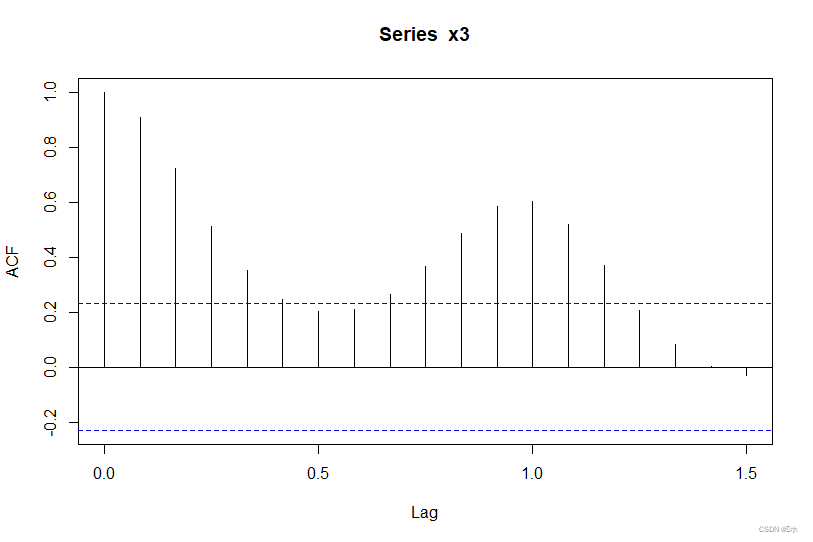
自相关图:
显示大部分的自相关系数在2倍标准差范围之外,可认为该自相关数很大,显著非零。可以判断该序列是非序列平稳。
单位根检验:
检验结果显示该序列可认为是平稳序列(带漂移项1阶滞后模型和既有漂移项又有趋势项的1-3阶滞后模型的P值小于0.05)。
Augmented Dickey-Fuller Test
alternative: stationary
Type 1: no drift no trend
lag ADF p.value
[1,] 0 0.770 0.861
[2,] 1 0.277 0.720
[3,] 2 0.417 0.760
[4,] 3 0.448 0.769
Type 2: with drift no trend
lag ADF p.value
[1,] 0 -1.63 0.472
[2,] 1 -4.16 0.010
[3,] 2 -2.43 0.164
[4,] 3 -1.64 0.465
Type 3: with drift and trend
lag ADF p.value
[1,] 0 -2.49 0.368
[2,] 1 -8.69 0.010
[3,] 2 -6.03 0.010
[4,] 3 -5.25 0.010
----
Note: in fact, p.value = 0.01 means p.value <= 0.01
2.白噪声检验:
延迟6阶和延迟12阶的LB统计量的P值为都小于α=0.05,则接受原假设,认为序列不是白噪声序列。
Box-Ljung test
data: x3
X-squared = 139.5, df = 6, p-value < 2.2e-16
Box-Ljung test
data: x3
X-squared = 139.5, df = 6, p-value < 2.2e-16
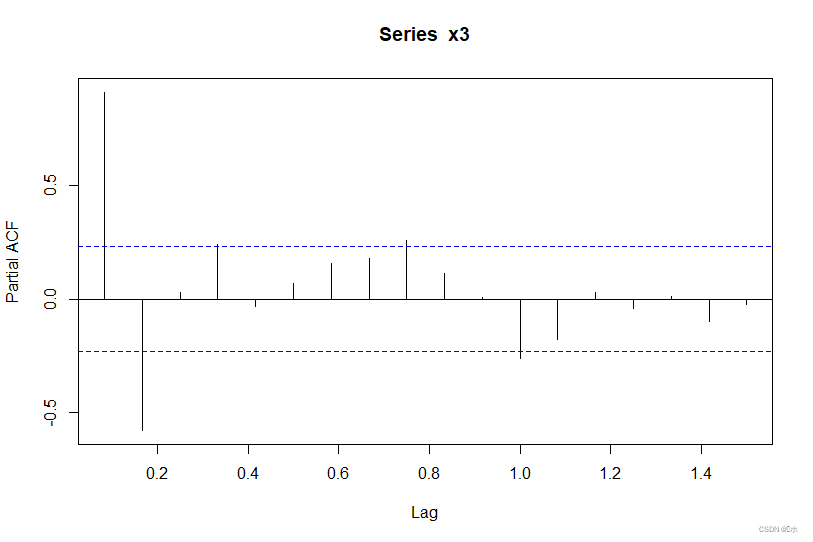
3.偏自相关图:
除了延迟1阶的偏自相关系数非常显著地≠0,之后其他阶数的偏自相关系数都迅速地向0值靠拢,这是一个典型的相关系数1阶结尾特征。
需要本练习原始数据请自行跳转下载:
博文:‘平稳性检验和ARMA模型的识别与定阶’训练数据资源-CSDN文库

Redis分布式缓存(三)Redis分片集群的搭建和原理分析)













)

![ORA-00600: internal error code, arguments: [krbcbp_9]](http://pic.xiahunao.cn/ORA-00600: internal error code, arguments: [krbcbp_9])
![[Linux][进程控制][进程程序替换]详细解读](http://pic.xiahunao.cn/[Linux][进程控制][进程程序替换]详细解读)
