今日任务:
1)62.不同路径
2)63.不同路径 II
3)复习day10
62.不同路径
题目链接:62. 不同路径 - 力扣(LeetCode)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。 问总共有多少条不同的路径?示例 1: 输入:m = 3, n = 7 输出:28示例 2: 输入:m = 2, n = 3 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 向右 -> 向右 -> 向下 向右 -> 向下 -> 向右 向下 -> 向右 -> 向右示例 3: 输入:m = 7, n = 3 输出:28示例 4: 输入:m = 3, n = 3 输出:6提示: 1 <= m, n <= 100 题目数据保证答案小于等于 2 * 10^9
文章讲解:代码随想录 (programmercarl.com)
视频讲解:动态规划中如何初始化很重要!| LeetCode:62.不同路径哔哩哔哩bilibili
思路:
机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。
按照动规五部曲来分析:
1)确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
2)确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1]。
此时在回顾一下 dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理。
那么很自然,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
3)dp数组的初始化
如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
class Solution:def uniquePaths(self, m: int, n: int) -> int:# 创建一个二维列表用于存储唯一路径数dp = [[0] * n for _ in range(m)]# 设置第一行和第一列的基本情况for i in range(m):dp[i][0] = 1for j in range(n):dp[0][j] = 1# 计算每个单元格的唯一路径数for i in range(1, m):for j in range(1, n):dp[i][j] = dp[i - 1][j] + dp[i][j - 1]# 返回右下角单元格的唯一路径数return dp[m - 1][n - 1]# dp2def uniquePaths2(self, m: int, n: int) -> int:# 创建一个一维列表用于存储每列的唯一路径数,初始化为1dp = [1] * n# 计算每个单元格的唯一路径数for j in range(1, m):for i in range(1, n):dp[i] += dp[i - 1]# 返回右下角单元格的唯一路径数return dp[n - 1]63.不同路径 II
题目链接:63. 不同路径 II - 力扣(LeetCode)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。 现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?示例 1: 输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]] 输出:2 解释:3x3 网格的正中间有一个障碍物。 从左上角到右下角一共有 2 条不同的路径: 1. 向右 -> 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 -> 向右示例 2: 输入:obstacleGrid = [[0,1],[0,0]] 输出:1提示: m == obstacleGrid.length n == obstacleGrid[i].length 1 <= m, n <= 100 obstacleGrid[i][j] 为 0 或 1
文章讲解:代码随想录 (programmercarl.com)
视频讲解:动态规划,这次遇到障碍了| LeetCode:63. 不同路径 II哔哩哔哩bilibili
思路:
- 创建一个二维列表
dp用于存储路径数,其中dp[i][j]表示到达网格(i, j)处的唯一路径数。- 首先判断起点和终点是否有障碍物,如果起点或终点有障碍物,则直接返回0,因为无法到达终点。
- 初始化
dp[0][0],如果起点没有障碍物,则路径数为1,否则为0。- 对于其他位置
(i, j),如果当前位置有障碍物,则路径数为0,否则路径数等于上方和左方单元格的路径数之和。- 最后返回终点的路径数,即
dp[m - 1][n - 1]。
class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:m = len(obstacleGrid) # 网格的行数n = len(obstacleGrid[0]) # 网格的列数if obstacleGrid[m - 1][n - 1] == 1 or obstacleGrid[0][0] == 1:# 如果起点或终点有障碍物,直接返回0return 0dp = [[0] * n for _ in range(m)] # 创建一个二维列表用于存储路径数# 设置起点的路径数为1dp[0][0] = 1 if obstacleGrid[0][0] == 0 else 0# 计算第一列的路径数for i in range(1, m):if obstacleGrid[i][0] == 0:dp[i][0] = dp[i - 1][0]# 计算第一行的路径数for j in range(1, n):if obstacleGrid[0][j] == 0:dp[0][j] = dp[0][j - 1]# 计算其他位置的路径数for i in range(1, m):for j in range(1, n):if obstacleGrid[i][j] == 1:continuedp[i][j] = dp[i - 1][j] + dp[i][j - 1]return dp[m - 1][n - 1] # 返回终点的路径数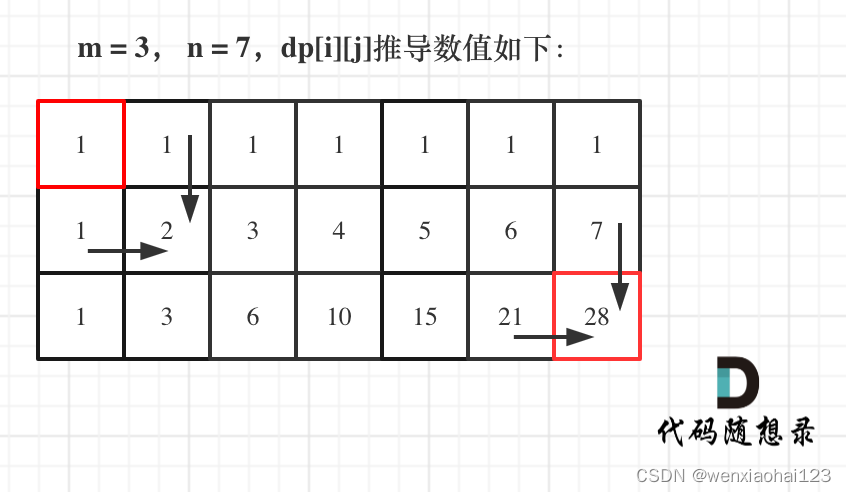


![Missing artifact org.opencv:opencv:jar:4.10.0 [opencv-4.10.0.jar]](http://pic.xiahunao.cn/Missing artifact org.opencv:opencv:jar:4.10.0 [opencv-4.10.0.jar])
![[HDFS 相关Shell命令]](http://pic.xiahunao.cn/[HDFS 相关Shell命令])
)


—— 使用感知器进行图像分类)
——垃圾回收)
介绍)
(含2022年和2023年))









)