本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

给你一份航线列表 tickets ，其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。

所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。

• 例如，行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小，排序更靠前。

假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次 。

示例 1：

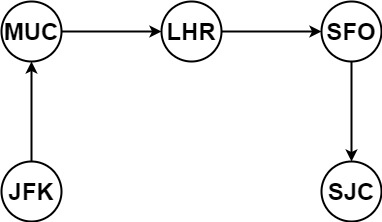
输入：tickets = [["MUC","LHR"],["JFK","MUC"],["SFO","SJC"],["LHR","SFO"]]
输出：["JFK","MUC","LHR","SFO","SJC"]

示例 2：

输入：tickets = [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
输出：["JFK","ATL","JFK","SFO","ATL","SFO"]
解释：另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"] ，但是它字典排序更大更靠后。

提示：

• 1 <= tickets.length <= 300
• tickets[i].length == 2
• fromi.length == 3
• toi.length == 3
• fromi 和 toi 由大写英文字母组成
• fromi != toi

---

本题和「753. 破解保险箱」类似，是力扣平台上为数不多的求解欧拉回路 / 欧拉通路的题目。

我们化简本题题意：给定一个 $O(n)$ 个点 $O(m)$ 条边的图，要求从指定的顶点出发，经过所有的边恰好一次（可以理解为给定起点的「一笔画」问题），使得路径的字典序最小。这种「一笔画」问题与欧拉图或者半欧拉图有着紧密的联系，下面给出定义：

• 通过图中所有边恰好一次且行遍所有顶点的通路称为欧拉通路；
• 通过图中所有边恰好一次且行遍所有顶点的回路称为欧拉回路；
• 具有欧拉回路的无向图称为欧拉图；
• 具有欧拉通路但不具有欧拉回路的无向图称为半欧拉图。

因为本题保证至少存在一种合理的路径，也就告诉了我们，这张图是一个欧拉图或者半欧拉图。我们只需要输出这条欧拉通路的路径即可。如果没有保证至少存在一种合理的路径，我们需要判别这张图是否是欧拉图或者半欧拉图，具体地：

• 对于无向图 $G$ ，$G$ 是欧拉图当且仅当 $G$ 是连通的且没有奇度顶点。
• 对于无向图 $G$ ，$G$ 是半欧拉图当且仅当 $G$ 是连通的且 $G$ 中恰有 $0$ 个或 $2$ 个奇度顶点。
• 对于有向图 $G$ ，$G$ 是欧拉图当且仅当 $G$ 的所有顶点属于同一个强连通分量且每个顶点的入度和出度相同。
• 对于有向图 $G$ ，$G$ 是半欧拉图当且仅当：
  • 如果将 $G$ 中的所有有向边退化为无向边时，那么 $G$ 的所有顶点属于同一个强连通分量；
  • 最多只有一个顶点的出度与入度差为 $1$ ；
  • 最多只有一个顶点的入度与出度差为 $1$ ；
  • 所有其他顶点的入度和出度相同。

让我们考虑下面的这张图：

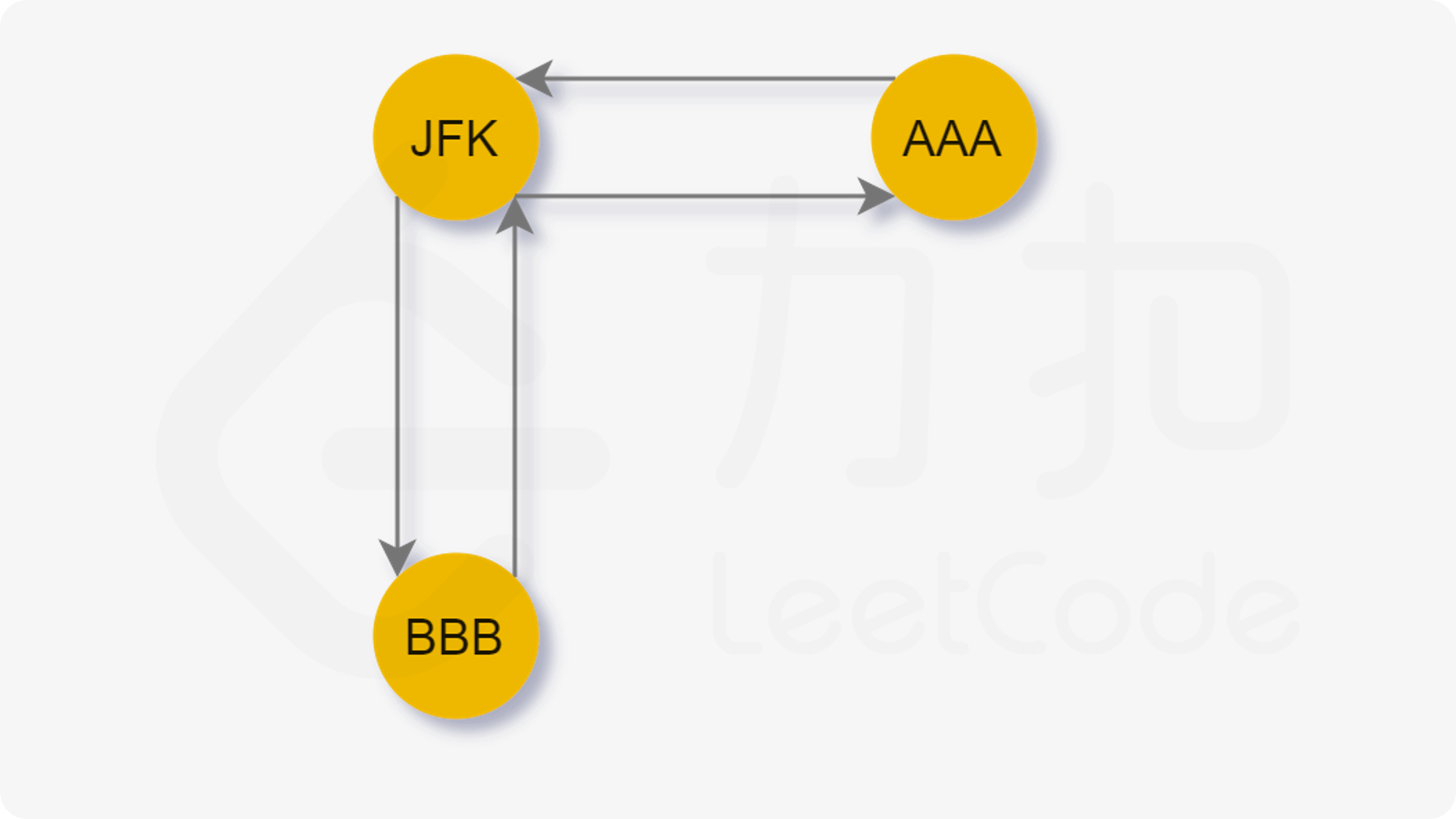
我们从起点 $JFK$ 出发，合法路径有两条：

• $JFK\to AAA\to JFK\to BBB\to JFK$
• $JFK\to BBB\to JFK\to AAA\to JFK$

既然要求字典序最小，那么我们每次应该贪心地选择当前节点所连的节点中字典序最小的那一个，并将其入栈。最后栈中就保存了我们遍历的顺序。

为了保证我们能够快速找到当前节点所连的节点中字典序最小的那一个，我们可以使用优先队列存储当前节点所连到的点，每次我们 $O(1)$ 地找到最小字典序的节点，并 $O(\log m)$ 地删除它。

然后我们考虑一种特殊情况：

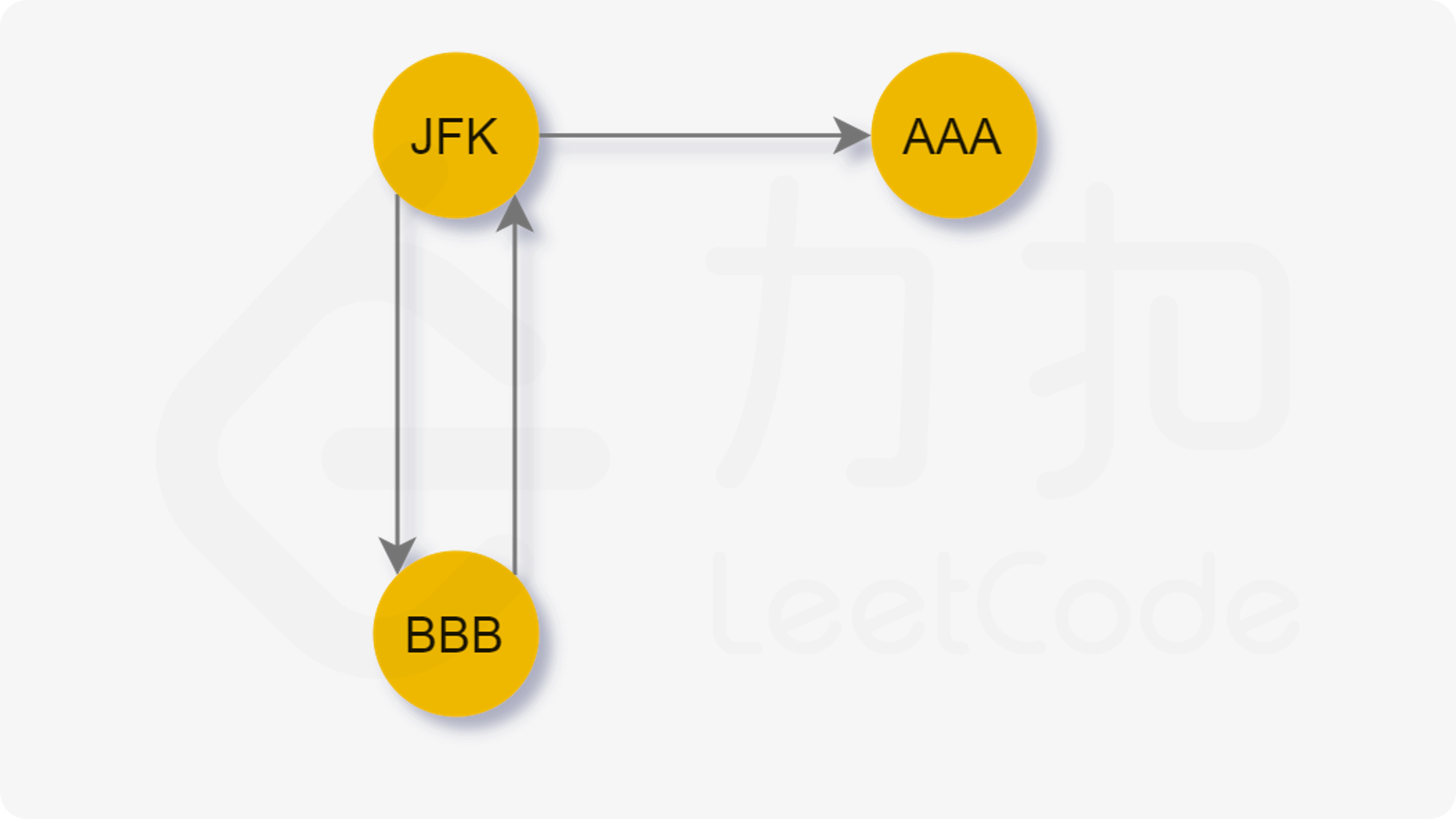
当我们先访问 $AAA$ 时，我们无法回到 $JFK$，这样我们就无法访问剩余的边了。也就是说，当我们贪心地选择字典序最小的节点前进时，我们可能先走入「死胡同」，从而导致无法遍历到其他还未访问的边。于是我们希望能够遍历完当前节点所连接的其他节点后再进入「死胡同」。

注意对于每一个节点，它只有最多一个「死胡同」分支。依据前言中对于半欧拉图的描述，只有那个入度与出度差为 $1$ 的节点会导致死胡同。

---

解法 $Hierholzer$ 算法

$Hierholzer$ 算法用于在连通图中寻找欧拉路径，其流程如下：

1. 从起点出发，进行深度优先搜索。
2. 每次沿着某条边从某个顶点移动到另外一个顶点时，都需要删除这条边。
3. 如果没有可移动的路径，则将所在节点加入到栈中，并返回。

当我们顺序地考虑该问题时，我们也许很难解决该问题，因为我们无法判断当前节点的哪一个分支是「死胡同」分支。不妨倒过来思考。我们注意到只有那个入度与出度差为 $1$ 的节点会导致死胡同。而该节点必然是最后一个遍历到的节点——对于当前节点而言，走入它的每一个非「死胡同」分支进行深度优先搜索，都将会搜回到当前节点。而从它的「死胡同」分支出发进行深度优先搜索将不会搜回到当前节点。我们可以改变入栈的规则，当遍历完一个节点所连的所有节点后，才将该节点入栈（即逆序入栈），也就是说当前节点的死胡同分支始终优先于其他非「死胡同」分支入栈。

这样就能保证我们可以「一笔画」地走完所有边，且最终的栈中逆序地保存了「一笔画」的结果。我们只要将栈中的内容反转，即可得到答案。

class Solution {
public:unordered_map<string, priority_queue<string, vector<string>, std::greater<string>>> vec;vector<string> stk;void dfs(const string& curr) {while (vec.count(curr) && vec[curr].size() > 0) {string tmp = vec[curr].top();vec[curr].pop();dfs(move(tmp));}stk.emplace_back(curr);}vector<string> findItinerary(vector<vector<string>>& tickets) {for (auto& it : tickets) {vec[it[0]].emplace(it[1]);}dfs("JFK"); // JFK要么是欧拉回路的一点,要么是欧拉通路的起点 reverse(stk.begin(), stk.end());return stk;}
};

复杂度分析：

• 时间复杂度：$O(m\log m)$ ，其中 $O(m)$ 是边的数量。对于每一条边我们需要 $O(\log m)$ 地删除它，最终的答案序列长度为 $m+1$ ，而与 $O(n)$ 无关。
• 空间复杂度：$O(m)$ ，其中 $O(m)$ 是边的数量。我们需要存储每一条边。