目录

王道考研ppt：

个人理解：

手算整数的除法：

​编辑

手算二进制的除法：

用机器实现除法：

方法一：恢复余数法

第二种方法：加减交替法

---

王道考研ppt：

个人理解：

手算整数的除法：

将除数的小数点移动到最右边，被除数跟着移动。
之后，对于每一次的余数，减去，用除数乘以商的积，要保证每一次的积尽可能的接近余数，但是又不能大于被除数
如此循环，直到最后的余数为0

手算二进制的除法：

和整数的除法是一样的
只是多了一个区别，那就是商只能取0或者1
所以，就不需要考虑商和除数的积是否尽可能接近被除数的情况
因为就只有商的可能取值：要么0，要么1
所以，相对更加简单

用机器实现除法：

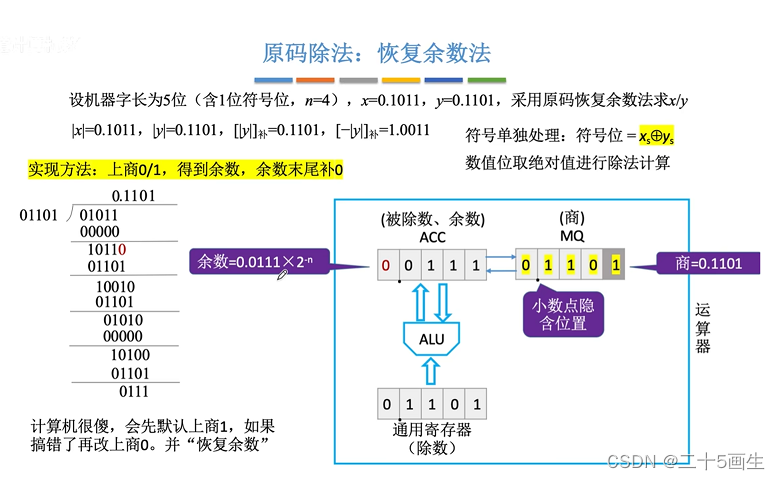
方法一：恢复余数法

因为所有正负整数、正负小数都可以转化为二进制，所以机器只需要解决二进制的除法计算，就可以解决所有数据的计算
所以需要处理二进制的除法计算
机器处理二进制需要是四个期间：
ACC：存储被除数和余数
通用寄存器：存余数
ALU：进行计算，从ACC拿到余数/被除数和余数，进行减法运算
MQ：存商

四个器件的处理过程如下：
将被除数存到ACC中，除数存到通用寄存器中
然后在MQ的最低位默认为当前计算的商（注意，默认为1）
然后，取商1，和通用寄存器的除数相乘，得到积，传给ALU
ACC将被除数传到ALU
ALU对被除数和商*除数的积进行相减
得到结果再返回给ACC
ACC再判断减的结果如果是负数，说明商应该为0
于是，传信息给MQ，将商从1改为0
同时，余数也要恢复
于是，ACC再将这个负数的余数传到ALU，通用寄存器也把除数再次传到ALU，二者相加
回复到原来没有被减去除数的要被除数/余数
之后，整个ACC和MQ向左移动一位
于是，ACC更新为新的余数，MQ更新为新的商结果
持续以上的处理循环，当ACC的余数部分为0时，计算结束
或者当达到计算精度要求时，计算结束

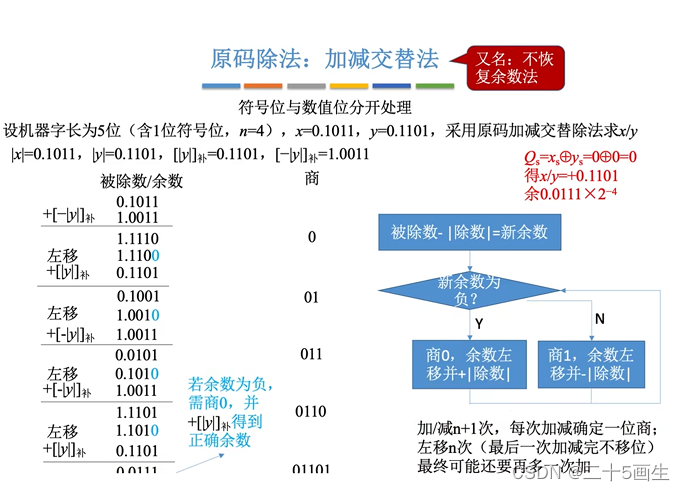
第二种方法：加减交替法

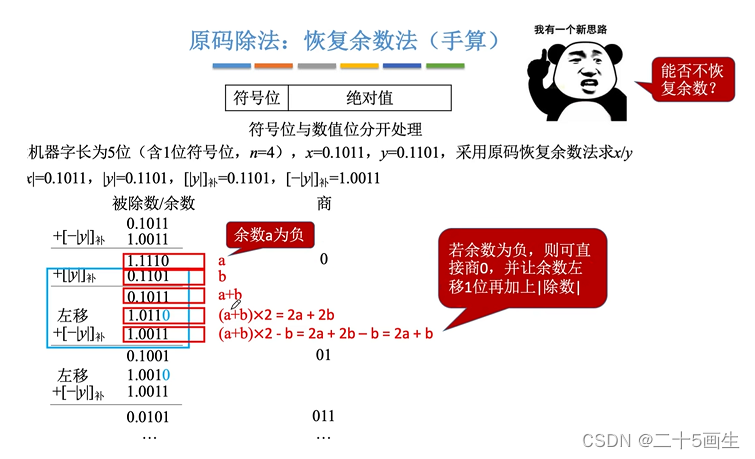
该方法是方法一的改进
方法一的商默认为1，当商应该为0时，需要对当前的余数加上除数恢复到原来的余数这样的一个处理
所以，比较麻烦，还需要再回去一次
那么，是不是可以改进这一点呢？
可以

假设当前余数为a
除数为b
恢复的处理是：a + b 
也就是说，原来的余数应该是a + b
然后商恢复为0
再进行下一位的计算
左移：2(a+b)
商设置为1，再减去b除数
得到下一个位置的余数：2(a+b)-b=2a+b

有了以上的推理，我们就可以实现：
当余数为负数时，
1、调整当前商为0
2、调整下一个位置的商为1
3、全部左移一位
4、当前余数直接*2 + 除数 ，直接得到下一步计算的余数
一箭三雕，得到了当前位的商0，得到下一个位置的商，得到下一个位的余数
妙哉

但是这里有一个问题：
如果是定点小数的除法，结果也只能是定点小数，也就是不能表示大于1的数
也就是说，被除数必须比除数小
那么，机器是怎么检测的呢？
很简单，
如果商的第一位是1，那就说明被除数比除数大，直接中断计算