738.单调递增的数字
当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。
示例 1:
输入: n = 10 输出: 9
示例 2:
输入: n = 1234 输出: 1234
示例 3:
输入: n = 332 输出: 299
思路
首先想到暴力法,超时
暴力(超时)
class Solution {public int monotoneIncreasingDigits(int n) {if(judge(n)){return n;}else{for(int i = n-1; i > 0; i--){if(judge(i)){return i;}}}return 0;}public boolean judge(int n){String s = String.valueOf(n);char [] c = s.toCharArray();for(int i=1; i < c.length; i++){if(c[i] >= c[i-1]){continue;}else{return false;}}return true;}
}贪心
贪心策略;拿一个两位的数字来举例。
例如:98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]--,然后strNum[i]给为9,这样这个整数就是89,即小于98的最大的单调递增整数。
然后判断遍历方向,从前往后还是从后往前。
从前往后会出现如下问题:
如332:变化如下 332 -> 329 -> 将第二个3 -- 变为2 导致它小于第一个3了。
这是因为从前往后没用到上次比较得出的结果,从后往前:332 -> 329 -> 299
class Solution {public int monotoneIncreasingDigits(int n) {if(judge(n)){return n;}else{String s = String.valueOf(n);char [] c = s.toCharArray();int start = 0;for(int i = c.length - 1; i > 0; i--){if(c[i-1] > c[i]){c[i-1] = (char)(c[i-1] - 1);start = i;}}for(int i = start; i<c.length; i++){c[i] = '9';}return Integer.parseInt(String.valueOf(c));}}public boolean judge(int n){String s = String.valueOf(n);char [] c = s.toCharArray();for(int i=1; i < c.length; i++){if(c[i] >= c[i-1]){continue;}else{return false;}}return true;}
}总结
本题只要想清楚个例,例如98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]减一,strNum[i]赋值9,这样这个整数就是89。就可以很自然想到对应的贪心解法了。
想到了贪心,还要考虑遍历顺序,只有从后向前遍历才能重复利用上次比较的结果。
最后代码实现的时候,也需要一些技巧,例如用一个flag来标记从哪里开始赋值9。
968.监控二叉树
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
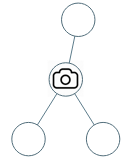
输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
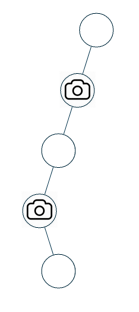
输入:[0,0,null,0,null,0,null,null,0] 输出:2 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
思路
首先明确 如何放置摄像头才能让总体数量最小:
可以发现,示例中的摄像头都没有放在叶子节点上,摄像头可以覆盖上中下三层,如果放在叶子节点上就会浪费一层,所以应当把摄像头放在叶子节点的父节点位置。
那么为什么不从头节点开始看,而是从叶子节点看呢?头节点不放 只能省下一个,而叶子节点不放,省下的摄像头是指数级别的。
所以,从下往上看,局部最优:让叶子节点的父节点安放摄像头,所用摄像头最少,整体最优:全部摄像头最少。
此时,大概思路:从下往上,先给叶子节点的父节点安放摄像头,然后隔两个节点放一个摄像头,直至到二叉树头结点。
那么剩下两个难点:
1、二叉树从下往上遍历
2、如何隔两个节点放一个摄像头
1:后序遍历,左右中,并且因为需要搜索整棵树,采用递归函数搜索整棵树的写法。
2:利用状态转移的公式。记录三种状态,0-无覆盖,1-有摄像头,2-有覆盖。
首先 空节点只能是有覆盖状态,因为:为了让摄像头数量最少,我们要尽量让叶子节点的父节点安装摄像头,这样才能摄像头的数量最少。那么空节点不能是无覆盖的状态,这样叶子节点就要放摄像头了,空节点也不能是有摄像头的状态,这样叶子节点的父节点就没有必要放摄像头了,而是可以把摄像头放在叶子节点的爷爷节点上。
所以空节点的状态只能是有覆盖,这样就可以在叶子节点的父节点放摄像头了
递归后序遍历,终止条件即为遇到空节点,同时返回状态值 2 有覆盖
然后利用递归搜索整棵树的模板,定义代表左右子树状态值的int数 left right,进行后序遍历、
单层递归逻辑:
有如下四类情况:(三种状态,0-无覆盖,1-有摄像头,2-有覆盖。)
①当left为2 right也为2时,此时root应返回 0 无覆盖
②当left right至少有一个为 0 无覆盖时,此时root返回 1 有摄像头
③当left right 至少有一个为1 有摄像头时,此时root返回 2 有覆盖
④当根节点 状态为 0 res++;
注意上述顺序种 ③中的部分逻辑 如(1,0)左节点有摄像头,右节点无覆盖
提前在②中 处理,因为需满足所有节点被覆盖。
代码
class Solution {public int res = 0;public int minCameraCover(TreeNode root) {//根节点无覆盖,此时需在根节点加一个if(tracing(root) == 0) {res++;}return res;}/*0 无覆盖1 有摄像头2 有覆盖*/public int tracing(TreeNode root){//空结点,默认有覆盖if(root == null) return 2;int left = tracing((root.left));int right = tracing(root.right);//左右状态共九种//左右都有覆盖,此时节点为无覆盖if(left == 2 && right == 2){//(2,2)return 0;}else//左右至少有一个是无覆盖的,那么应该返回1,在此节点处放摄像头if(left == 0 || right == 0){// (0,0) (0,1) (0,2) (1,0) (2,0)// 状态值为 1 摄像头数 ++;res++;return 1;}else{//左右至少有一个是有摄像头的,此时节点为有覆盖//(1,1) (1,2) (2,1)return 2;}}
}总结
贪心思路:局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,整体最优:全部摄像头数量所用最少!
求解:后序遍历整棵树 + 状态转移 + 单层递归情况分解
贪心总结
首先贴一个图: 来自代码随想录 (programmercarl.com)
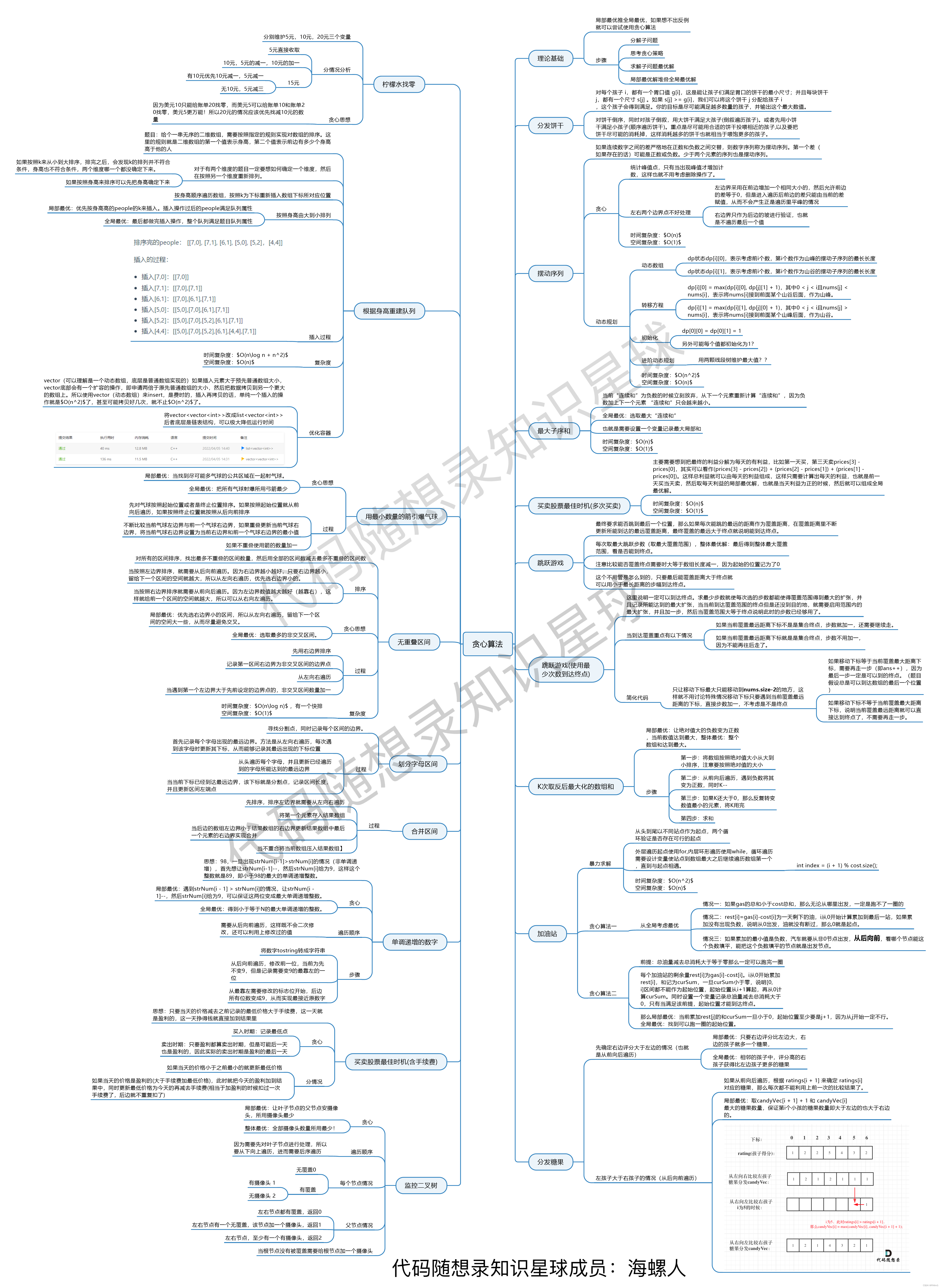
开始复习以往做过的题目,计划通过类似方式对做过的题目进行总结归纳。





)
)
)
)










