C++ 模拟实现 STL 中的 set、map 与 multiset、multimap

一，RB_tree 的实现

1，RB_tree 的节点与数据结构

2，RB_tree 的迭代器

3，RB_tree 的构造

4，RB_tree 的元素操作

5，完整代码

二，set 与 multiset 的实现

1，set

2，multiset

三，map 与 multimap 的实现

1，map

2，multimap

set 与 map 是 STL 中的关联式容器，这俩容器与它们的衍生体 multiset 与 multimap 的底层都是由 RB_tree（红黑树）来实现的，虽然红黑树也是一个独立的容器，但是 STL 并没有将其开放给外界使用。关于 set、map 与 multiset、multimap 的使用方法这里就不介绍了，此文主要是简单的模拟实现。

在实现这两大容器之前，我们需要先实现它们的底层容器：红黑树；如果不清楚什么是红黑树或者不清楚红黑树的底层是怎么实现的，可以看看这篇博客：

红黑树详解（C++ 实现）-CSDN博客文章浏览阅读871次，点赞23次，收藏18次。红黑树，是一种，每个结点上都有一个存储位以表示结点的颜色（红或黑）。通过对任何一条从根到叶子的路径上各个结点的着色方式的限制，它能够在插入和删除节点时自动调整树的结构，以保持树的平衡，从而保证查找、插入和删除操作的时间复杂度始终为O(logN)。https://blog.csdn.net/qq_41521068/article/details/134833750?spm=1001.2014.3001.5501

这里就默认大家都比较熟悉红黑树的底层实现了。下面此文将基于上面这篇博客所实现的红黑树来进行一下小小的改造，使其能够为 set、map 与 multiset、multimap 所用。为了方便表述，本文将把上面博客实现的红黑树叫做 “原始红黑树”，将改造后的红黑树叫做 “RB_tree”。

一，RB_tree 的实现

1，RB_tree 的节点与数据结构

节点的设计与原始红黑树一样：

enum Color { Red, Black };template<class T>
struct RBTreeNode {Color color;T val;RBTreeNode* left, * right, * parent;RBTreeNode(T val_, Color color_ = Red):val(val_), color(color_), left(nullptr), right(nullptr), parent(nullptr) {}
};

RB_tree 的数据结构与原始红黑树有两个很大的区别：

① RB_tree 维护了一个头节点（head），我们让 head->left 指向整个树中最靠左边的节点，让 head->right 指向整个树中最靠右边的节点，而 head->parent 则指向根节点，

root->parent 要指向 head（头节点与根节点的 parent 互相指向对方）。我们需要在每一次插入以及删除时动态的去维护这个 head 节点。

② RB_tree 模板参数比原始红黑树要复杂一点，RB_tree 需要 Key, Val, KeyOfVal, Compare 四个参数（这里偷一下懒，空间配置器就直接省略了）。KeyOfVal 与 Compare 都是函数类型，它们具体是用来干什么的，我们稍后再说~

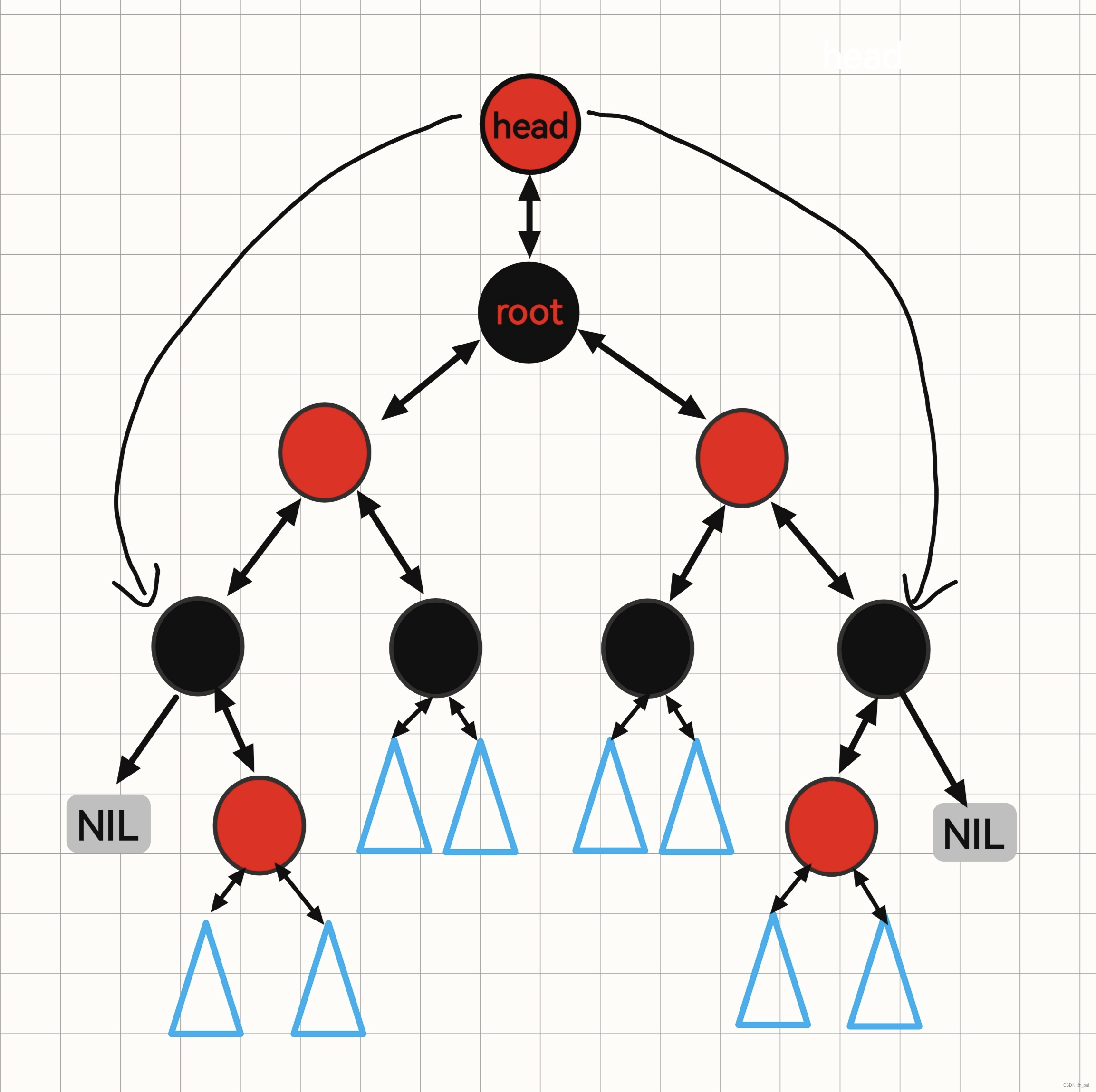
设计一个头节点可以更好的辅助我们处理边界情况，尤其是在处理迭代器的 ++ 与 -- 操作的时候，稍后我们实现迭代器时就能感受到了。

RB_tree 的结构

template<class Key, class Val, class KeyOfVal, class Compare>
class RBTree {// ...
private:typedef RBTreeNode<Val> Node;typedef Node* link_type;private:KeyOfVal _kov;Compare _cmp;size_t _size;link_type _head;private:// 返回根节点link_type& root()const { return _head->parent; }// 为了方便比较键值 key 而设计的函数bool key_compare(link_type node, const Val& val) {return _cmp(_kov(node->val), _kov(val));}bool key_equal(link_type node, const Val& val) {return _kov(node->val) == _kov(val);}// ...
};

现在我们来说说 KeyOfVal 与 Compare。

Ⅰ，Compare

Compare 的作用是定义了元素之间的比较规则，从而决定了红黑树中元素的排序方式，这样能方便我们更灵活的使用红黑树

Ⅱ，KeyOfVal

KeyOfVal 的作用是从存储的元素中提取出键值。红黑树存储的元素通常是键值对，它就是用来告诉红黑树如何从这些元素中提取出键值，以便进行比较和排序。
红黑树中存储的元素可能是键值对，也可能仅仅只是单键（ set 中存的是单键， map 中存的是键值对）。在红黑树中，只要涉及到比较就一定会使用到键，KeyOfVal 就是为了统一单键与键值对这两种情况而设计的。
在上面代码中的模板参数中，Key 表示键，Val 表示储存的元素；如果是 map，Val 表示一个 pair<key,val>键值对，如果是 set，Val 表示 Key。而 KeyOfVal 就是从 Val 中取出 Key

下面是一些 RB_tree 提供的简单的功能：

template<class Key, class Val, class KeyOfVal, class Compare>
class RBTree {// ...
public:// 简单的基础功能static bool is_black(link_type node) { return node == nullptr or node->color == Black; }static bool is_red(link_type node) { return node != nullptr and node->color == Red; }bool empty()const { return _size == 0; }size_t size()const { return _size; }void clear() {dfs_clear(root());_size = 0;_head->left = _head->right = _head;root() = nullptr;}private:// 最左边的节点link_type left_most(link_type node) {if (node == nullptr)return _head;while (node->left) {node = node->left;}return node;}// 最右边的节点link_type right_most(link_type node) {if (node == nullptr)return _head;while (node->right) {node = node->right;}return node;}// 将所有节点删除static void dfs_clear(link_type root) {if (root == nullptr) return;dfs_clear(root->left);dfs_clear(root->right);delete root;}// ...
};

2，RB_tree 的迭代器

要想将 RB_tree 实现成一个泛型容器，设计一个迭代器是至关重要的一步。如果不清楚什么是迭代器或者是不清楚要怎么为容器设计一个迭代器，可以看看这篇博客：

C++ 迭代器与反向迭代器-CSDN博客

以下是 RB_tree 迭代器所实现的功能：

template<class T, class Ref, class Ptr> // Ref: 引用类型 , Ptr: 指针类型
struct RBTreeIterator {typedef T	value_type;typedef Ref reference;typedef Ptr pointer;typedef RBTreeIterator<T, Ref, Ptr> self;	//当前迭代器typedef RBTreeIterator<T, T&, T*> iterator;	//普通迭代器typedef RBTreeNode<T> Node;typedef Node* link_type;	link_type _node;    // 迭代器所对应的节点类型RBTreeIterator(const iterator& iter) :_node(iter._node) {}	//普通迭代器构造当前迭代器RBTreeIterator(link_type node) :_node(node) {}				//红黑树节点构造迭代器reference operator*() { return _node->val; }pointer operator->() { return &(operator*()); }bool operator==(self iter) { return _node == iter._node; }bool operator!=(self iter) { return not(*this == iter); }self operator++();self operator++(int);self operator--();self operator--(int);};

这里的重点是 operator++（前进）与 operator--（后退）的实现。这里是按照的时中序遍历的顺序（即按照左 -> 根 -> 右的顺序）来进行前进或后退。

先来看看 operator++

template<class T, class Ref, class Ptr> // Ref: 引用类型 , Ptr: 指针类型
struct RBTreeIterator {// ...self operator++() {// 如果有右节点我们就一直走到整个右子树的最左端if (_node->right) {link_type node = _node->right;while (node->left) {node = node->left;}_node = node;}else {    // 如果没有右节点, 我们就向上回溯, 直到当前节点不是右节点link_type parent = _node->parent;link_type cur = _node;while (cur == parent->right) {cur = cur->parent;parent = cur->parent;}_node = cur;// 注意一下这个 if 语句, 这是一个特殊的情况, 稍后再画图解释// 我们在这标记为 情况一if (cur->right != parent)_node = parent;}return *this;}self operator++(int) {self res = *this;++(*this);return res;}// ...
}

再来看看 operator--

template<class T, class Ref, class Ptr> // Ref: 引用类型 , Ptr: 指针类型
struct RBTreeIterator {// ...self operator--() {// 注意一下这条 if 语句, 这是一个特殊情况, 稍后再画图演示// 我们在这标记为 情况二if (_node->color == Red and _node->parent->parent == _node) {_node = _node->right;}else if (_node->left) {	// 如果有左节点我们就一直走到整个左子树的最右端link_type node = _node->left;while (node->right) {node = node->right;}_node = node;}else {					//如果没有左节点, 我们就向上回溯, 直到当前节点不是左节点link_type parent = _node->parent;link_type cur = _node;while (cur == parent->left) {cur = cur->parent;parent = cur->parent;}_node = parent;}return *this;}self operator--(int) {self res = *this;--(*this);return res;}// ...
}

operator-- 操作与 operator++ 操作基本上是对称的，除了我们刚刚在注释中特别标明的特殊情况。

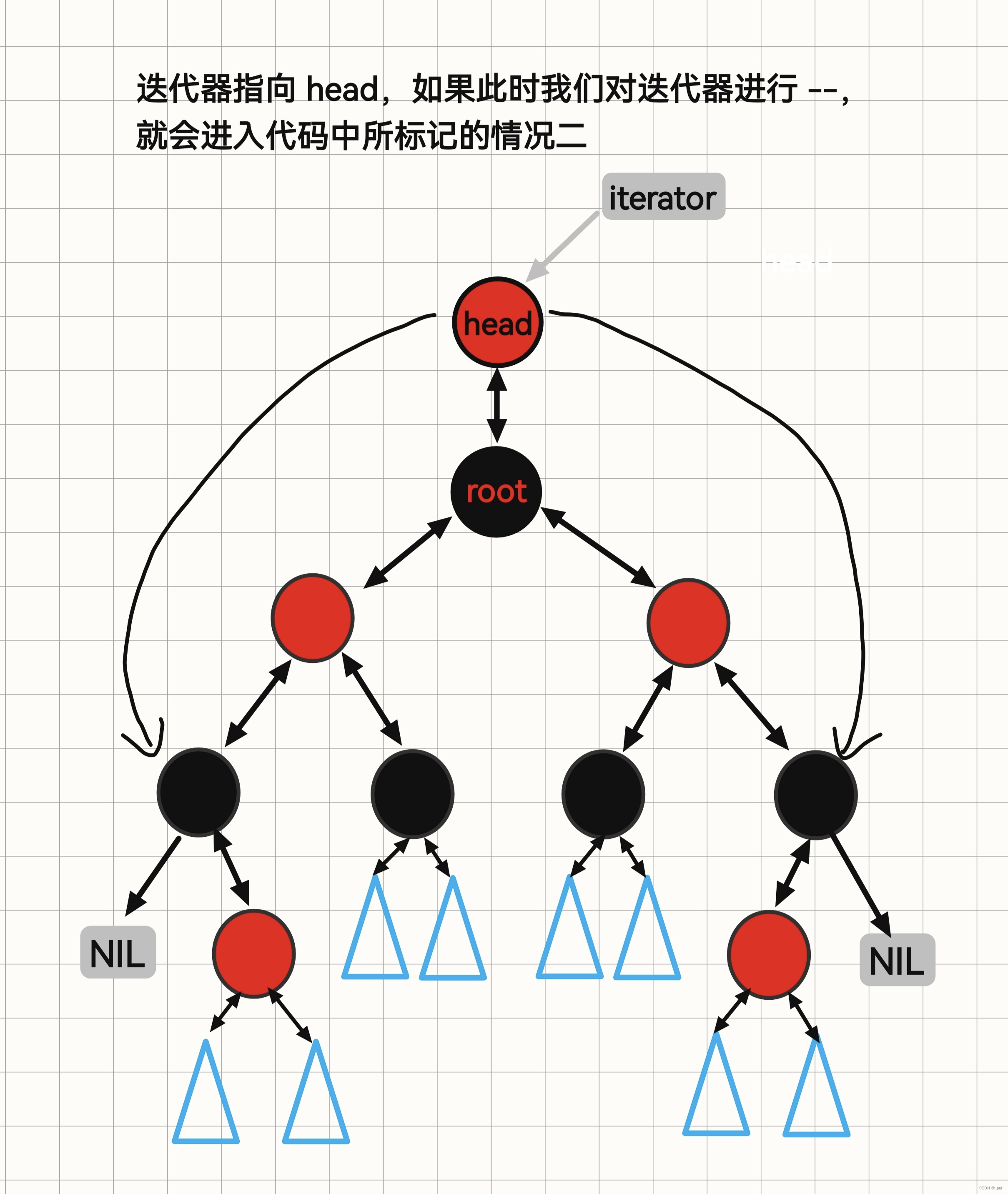
RB_tree 中的迭代器操作：

template<class Key, class Val, class KeyOfVal, class Compare>
class RBTree {// ...
public:// 迭代器类型typedef RBTreeIterator<Val, Val&, Val*>				iterator;typedef RBTreeIterator<Val, const Val&, const Val*> const_iterator;typedef Reverse_Iterator<iterator>					reverse_iterator;typedef Reverse_Iterator<const_iterator>			const_reverse_iterator;// begin 与 end 操作iterator begin() { return _head->left; }iterator end() { return _head; }const_iterator begin()const { return _head->left; }const_iterator end()const { return _head; }reverse_iterator rbegin() { return end(); }reverse_iterator rend() { return begin(); }const_reverse_iterator rbegin()const { return end(); }const_reverse_iterator rend()const { return begin(); }// ...
};

3，RB_tree 的构造

template<class Key, class Val, class KeyOfVal, class Compare>
class RBTree {// ...
private:// 初始化void init() {_head = new Node(Val(), Red);	// 为了与根节点区分，使用红色标记_head->left = _head;			// 初始化将 _head 的左节点与右节点都指向自己_head->right = _head;root() = nullptr;_size = 0;}
public:// 构造RBTree() {init();}RBTree(const RBTree& rbt) {init();for (const auto& data : rbt) insert_equal(data);}// ...
};

4，RB_tree 的元素操作

这里就说说 insert、erase、find 操作，关于红黑树的插入和删除逻辑这里就不再多说了，文章开头推荐的博客中有详细的演示与说明。

首先是 insert，RB_tree 中提供两种不同的插入方式：一种是 insert_unique()，表示插入的元素必须是树中不存在的元素；另一种是 insert_equal()，这个操作可以将重复的元素插入树中。这两种插入方式分别会被 set、map 与 multiset、multimap 调用。

具体代码：

template<class Key, class Val, class KeyOfVal, class Compare>
class RBTree {// ...
public:iterator insert_equal(const Val& val) {link_type parent = _head;link_type cur = root();while (cur) {parent = cur;cur = key_compare(cur, val) ? cur->right : cur->left;}return insert_assist(parent, val);}// 如果插入成功，返回值中的 second 为 true，否则为 falsepair<iterator, bool> insert_unique(const Val& val) {link_type parent = _head;link_type cur = root();while (cur) {parent = cur;cur = key_compare(cur, val) ? cur->right : cur->left;}if (key_equal(parent, val))return make_pair(end(), false);return make_pair(insert_assist(parent, val), true);}// ...
};

这两种插入方式在具体实现上十分相似，它们在最后都会调用 insert_assist()，其实 insert_unique() 与 insert_equal() 更多的是负责查找与检查的工作，真正的插入逻辑是靠 insert_assist() 去实现。

template<class Key, class Val, class KeyOfVal, class Compare>
class RBTree {// ...
public:iterator insert_assist(link_type parent, const Val& val) {link_type newNode = new Node(val, Red);newNode->parent = parent;if (parent == _head) {root() = newNode;root()->color = Black;}else {// 将parent与新插入进来的节点进行连接if (key_compare(parent, val))parent->right = newNode;elseparent->left = newNode;// 修正节点if (is_red(parent))insert_adjust(newNode);    // 这个函数与原始红黑树中的调整函数基本一致}                                  // 因为代码量比较多，这里就不展示了，具体的实现++_size;                           // 会在下一小部分的完整代码中展示// 维护head节点_head->left = left_most(root());_head->right = right_most(root());return iterator(newNode);}// ...
};

接下来是 erase

template<class Key, class Val, class KeyOfVal, class Compare>
class RBTree {// ...
public:// erase 函数将树内所有键值为 key 的元素全部删除，返回删除的个数size_t erase(const Key& key) {int cnt = 0;while (erase_assist(key)) ++cnt;return cnt;}// ...
};

与 insert 操作类似，真正的删除逻辑是靠 erase_assist 去实现

template<class Key, class Val, class KeyOfVal, class Compare>
class RBTree {// ...
public:size_t erase_assist(const Key& key) {link_type node = root();	// node 将表示为要被删去的节点link_type child = nullptr;	// child 是替换被删除节点的位置的节点while (node != nullptr) {if (_kov(node->val) == key) {// 被删除的节点有左子节点也有右子节点的情况if (node->left and node->right) {link_type next = left_most(node->right);	// node 的后继节点// 注意一下下面三行语句，稍后会解释为什么要这样写//node->val = next->val;			// 这样写会报错node->val.~Val();					// new (&node->val) Val(next->val);	// node = next;}child = node->left ? node->left : node->right;break;}else if (_cmp(_kov(node->val), key))node = node->right;elsenode = node->left;}if (node == nullptr)return 0;// 将 child 与 node->parent 链接if (child != nullptr)child->parent = node->parent;if (node == root())root() = child;else {if (node == node->parent->left)node->parent->left = child;elsenode->parent->right = child;}// 调整if (is_black(node))erase_adjust(child, node->parent);	// 这个函数与原始红黑树中的调整函数基本一致delete node;							// 因为代码量比较多，这里就不展示了，具体的实现--_size;								// 会在下一小部分的完整代码中展示// 维护head节点_head->left = left_most(root());_head->right = right_most(root());return 1;}// ...
};

我们在代码中标注了三条语句：

//node->val = next->val;			// 这样写会报错
node->val.~Val();					// 
new (&node->val) Val(next->val);	//

这里来解释一下：在 STL 的 map、multimap 实现中，键值对类型是 pair<const Key, Val>。由于 pair 的第一个元素是 const 类型，标准的赋值操作符 operator= 不允许修改第一个元素的值，这就是为什么直接使用 node->val = next->val 会导致编译器报错。解决这个问题的一种方法是使用 “placement new” 和显式的析构函数调用来替换节点的值，而不是直接赋值，这样可以绕过 const 限制。

5，完整代码

namespace mySTL {enum Color { Red, Black };template<class T>struct RBTreeNode {Color color;T val;RBTreeNode* left, * right, * parent;RBTreeNode(T val_, Color color_ = Red):val(val_), color(color_), left(nullptr), right(nullptr), parent(nullptr) {}};template<class T, class Ref, class Ptr> // Ref: 引用类型 , Ptr: 指针类型struct RBTreeIterator {typedef T	value_type;typedef Ref reference;typedef Ptr pointer;typedef RBTreeIterator<T, Ref, Ptr> self;	//当前迭代器typedef RBTreeIterator<T, T&, T*> iterator;	//普通迭代器typedef RBTreeNode<T> Node;typedef Node* link_type;	link_type _node;RBTreeIterator(const iterator& iter) :_node(iter._node) {}	//普通迭代器构造当前迭代器RBTreeIterator(link_type node) :_node(node) {}				//红黑树节点构造迭代器reference operator*() { return _node->val; }pointer operator->() { return &(operator*()); }bool operator==(self iter) { return _node == iter._node; }bool operator!=(self iter) { return not(*this == iter); }self operator++() {if (_node->right) {link_type node = _node->right;while (node->left) {node = node->left;}_node = node;}else {link_type parent = _node->parent;link_type cur = _node;while (cur == parent->right) {cur = cur->parent;parent = cur->parent;}_node = cur;// 注意if (cur->right != parent)	_node = parent;}return *this;}self operator++(int) {self res = *this;++(*this);return res;}self operator--() {// 注意if (_node->color == Red and _node->parent->parent == _node) {_node = _node->right;}else if (_node->left) {link_type node = _node->left;while (node->right) {node = node->right;}_node = node;}else {link_type parent = _node->parent;link_type cur = _node;while (cur == parent->left) {cur = cur->parent;parent = cur->parent;}_node = parent;}return *this;}self operator--(int) {self res = *this;--(*this);return res;}};template<class Key, class Val, class KeyOfVal, class Compare>class RBTree {private:typedef RBTreeNode<Val> Node;typedef Node* link_type;private:KeyOfVal _kov;Compare _cmp;size_t _size;link_type _head;public:// 迭代器类型typedef RBTreeIterator<Val, Val&, Val*>				iterator;typedef RBTreeIterator<Val, const Val&, const Val*> const_iterator;typedef Reverse_Iterator<iterator>					reverse_iterator;typedef Reverse_Iterator<const_iterator>			const_reverse_iterator;// begin 与 end 操作iterator begin() { return _head->left; }iterator end() { return _head; }const_iterator begin()const { return _head->left; }const_iterator end()const { return _head; }reverse_iterator rbegin() { return end(); }reverse_iterator rend() { return begin(); }const_reverse_iterator rbegin()const { return end(); }const_reverse_iterator rend()const { return begin(); }private:// 简单的基础功能link_type& root()const { return _head->parent; }static bool is_black(link_type node) { return node == nullptr or node->color == Black; }static bool is_red(link_type node) { return node != nullptr and node->color == Red; }//static const Key& get_key(link_type node) { return _kov(node->val); }// 为了方便比较键值 key 而设计的函数bool key_compare(link_type node, const Val& val){ return _cmp(_kov(node->val), _kov(val));}bool key_equal(link_type node, const Val& val) {return _kov(node->val) == _kov(val);}// 最左边的节点link_type left_most(link_type node) {if (node == nullptr)return _head;while (node->left) {node = node->left;}return node;}// 最右边的节点link_type right_most(link_type node) {if (node == nullptr)return _head;while (node->right) {node = node->right;}return node;}// 将所有节点删除static void dfs_clear(link_type root) {if (root == nullptr) return;dfs_clear(root->left);dfs_clear(root->right);delete root;}public:// 简单的基础功能bool empty()const { return _size == 0; }size_t size()const { return _size; }void clear() {dfs_clear(root()); _size = 0;_head->left = _head->right = _head;root() = nullptr;}private:// 初始化void init() {_head = new Node(Val(), Red);	// 为了与根节点区分，使用红色标记_head->left = _head;			// 初始化将 _head 的左节点与右节点都指向自己_head->right = _head;root() = nullptr;_size = 0;}public:// 构造RBTree() {init();}RBTree(const RBTree& rbt) {init();for (const auto& data : rbt) insert_equal(data);}public:iterator find(const Key& key) const {link_type node = root();while (node) {node = _cmp(_kov(node->val), key) ? node->right : node->left;}return  node == nullptr ? end() : iterator(node);}iterator insert_equal(const Val& val) {link_type parent = _head;link_type cur = root();while (cur) {parent = cur;cur = key_compare(cur, val) ? cur->right : cur->left;}return insert_assist(parent, val);}pair<iterator, bool> insert_unique(const Val& val) {link_type parent = _head;link_type cur = root();while (cur) {parent = cur;cur = key_compare(cur, val) ? cur->right : cur->left;}if (key_equal(parent, val)) return make_pair(end(), false);return make_pair(insert_assist(parent, val), true);}size_t erase(const Key& key) {int cnt = 0;while (erase_assist(key)) ++cnt;return cnt;}//检查是否是正确的红黑树bool is_RBTree()const {//根节点为红色直接返回falseif (is_red(root())) return false;// 判断每条路径的黑节点数量以及红节点的child的颜色是否符合红黑树的性质std::function<pair<bool, int>(link_type)> cnt_color = [&](link_type node) {// first:判断结果  second:黑节点的数量if (node == nullptr) {return make_pair(true, 1);}if (is_red(node) and is_red(node->parent)) {return make_pair(false, -1);}auto [left_is, cnt1] = cnt_color(node->left);auto [right_is, cnt2] = cnt_color(node->right);return left_is and right_is and cnt1 == cnt2 ?make_pair(true, cnt1 + is_black(node)) :make_pair(false, -1);};// 判断中序遍历是否有序std::function<bool()> inorder = [&]() {std::vector<Key> ino;function<void(link_type)> inside_inorder = [&](link_type node) {if (node) {inside_inorder(node->left);ino.push_back(KeyOfVal()(node->val));inside_inorder(node->right);}};inside_inorder(root());for (int i = 0;i < ino.size();++i) {if (i > 0 and _cmp(ino[i], ino[i - 1]) and ino[i] != ino[i - 1])return false;// 这里可以控制是否输出中序遍历的结果// cout << ino[i] << ' ';}return true;};return cnt_color(root()).first and inorder();}private:// 左旋void rotate_left(link_type node) {link_type right = node->right;node->right = right->left;right->left = node;if (node->right) node->right->parent = node;link_type parent = node->parent;right->parent = parent;node->parent = right;if (parent == _head) root() = right; //更新root()节点else if (parent->left == node) parent->left = right;else parent->right = right;}// 右旋void rotate_right(link_type node) {link_type left = node->left;node->left = left->right;left->right = node;if (node->left) node->left->parent = node;link_type parent = node->parent;left->parent = parent;node->parent = left;if (parent == _head) root() = left;else if (parent->left == node) parent->left = left;else parent->right = left;}private:iterator insert_assist(link_type parent, const Val& val) {link_type newNode = new Node(val, Red);newNode->parent = parent;if (parent == _head) {root() = newNode;root()->color = Black;}else {// 将parent与新插入进来的节点进行连接if (key_compare(parent, val))parent->right = newNode;elseparent->left = newNode;// 修正节点if (is_red(parent))insert_adjust(newNode);}++_size;// 维护head节点_head->left = left_most(root());_head->right = right_most(root());return iterator(newNode);}// 插入的调节void insert_adjust(link_type node) {link_type parent = node->parent;while (parent != _head and parent->color == Red) {link_type grand = parent->parent; //这里的grand是一定存在的// 当前的节点在 grand 的左边if (parent == grand->left) {link_type uncle = grand->right;// 情况一// uncle存在且为红色if (is_red(uncle)) {parent->color = uncle->color = Black;grand->color = Red;//继续向上调整}// 情况二与情况三//uncle不存在或uncle为黑色else {// 将情况三转为情况二if (node == parent->right) {rotate_left(parent);//注意：这里旋转完后parent与node的父子关系交换了，所以要swap回来std::swap(parent, node);}rotate_right(grand);parent->color = Black;grand->color = Red;//调整结束break;}}// 当前的节点在 grand 的右边// parent==grand->right 与 parent==grand->left 的情况类似else {link_type uncle = grand->left;if (is_red(uncle)) {parent->color = uncle->color = Black;grand->color = Red;}else {if (node == parent->left) {rotate_right(parent);std::swap(parent, node);}rotate_left(grand);parent->color = Black;grand->color = Red;break;}}//将node更新为当前的祖父节点，继续循环调整node = grand;parent = node->parent;}//保证根节点必须是黑色root()->color = Black;}size_t erase_assist(const Key& key) {link_type node = root();	// node 将表示为要被删去的节点link_type child = nullptr;	// child 是替换被删除节点的位置的节点while (node != nullptr) {if (_kov(node->val) == key) {// 被删除的节点有左子节点也有右子节点的情况if (node->left and node->right) {link_type next = left_most(node->right);	// node 的后继节点// 注意一下下面三行语句，稍后会解释为什么要这样写//node->val = next->val;			// 这样写会报错node->val.~Val();					// new (&node->val) Val(next->val);	// node = next;}child = node->left ? node->left : node->right;break;}else if (_cmp(_kov(node->val), key))node = node->right;elsenode = node->left;}if (node == nullptr)return 0;// 将 child 与 node->parent 链接if (child != nullptr)child->parent = node->parent;if (node == root())root() = child;else {if (node == node->parent->left)node->parent->left = child;elsenode->parent->right = child;}// 调整if (is_black(node))erase_adjust(child, node->parent);delete node;--_size;// 维护head节点_head->left = left_most(root());_head->right = right_most(root());return 1;}// 删除的调节void erase_adjust(link_type node, link_type parent) {//cout << "start ";while (node != root() and is_black(node)) {// 当前的节点再 parent 的左边if (node == parent->left) {link_type sibling = parent->right;// 情况一if (is_red(sibling)) {//cout << "case1 ";rotate_left(parent);sibling->color = Black;parent->color = Red;sibling = parent->right;}// 情况二if (is_black(sibling->left) and is_black(sibling->right)) {//cout << "case2 ";sibling->color = Red;node = parent;parent = node->parent;continue;}else {// 情况三if (is_black(sibling->right)) {//cout << "case3 ";rotate_right(sibling);sibling->color = Red;parent->right->color = Black;sibling = parent->right;// 此时我们已将情况三转换为情况四}// 情况四//cout << "case4 ";sibling->color = parent->color;rotate_left(parent);parent->color = Black;sibling->right->color = Black;break;}}// 与上面的情况对称else {link_type sibling = parent->left;// 情况一if (is_red(sibling)) {//cout << "case1 ";rotate_right(parent);sibling->color = Black;parent->color = Red;sibling = parent->left;}// 情况二if (is_black(sibling->right) and is_black(sibling->left)) {//cout << "case2 ";sibling->color = Red;node = parent;parent = node->parent;continue;}else {// 情况三if (is_black(sibling->left)) {//cout << "case3 ";rotate_left(sibling);sibling->color = Red;parent->left->color = Black;sibling = parent->left;// 此时我们已将情况三转换为情况四}// 情况四//cout << "case4 ";sibling->color = parent->color;rotate_right(parent);parent->color = Black;sibling->left->color = Black;break;}}}//cout << "end ";if (node) node->color = Black;}};}

二，set 与 multiset 的实现

set 与 multiset 中的所有元素会根据元素的键值自动的排序，set 中的每一个元素都是独一无二的，而 multiset 允许出现重复的元素。set 与 multiset 不允许修改容器中的任何元素，因为如果修改了键值的大小，那么容器中的元素就不一定有序了。因此 set 系列的中的 iterator 被定义为 const_iterator，reverse_iterator 被定义成 const_reverse_iterator。

1，set

namespace mySTL {// settemplate<class Key, class Compare = less<Key>>class set {private:struct KeyOfVal {const Key& operator()(const Key& key) { return key; }};typedef RBTree<Key, Key, KeyOfVal, Compare> RBTree;RBTree _rbt;public:// 迭代器typedef typename RBTree::const_iterator			iterator;typedef typename RBTree::const_iterator			const_iterator;typedef typename RBTree::const_reverse_iterator reverse_iterator;typedef typename RBTree::const_reverse_iterator const_reverse_iterator;iterator begin()const { return _rbt.begin(); }iterator end()const { return _rbt.end(); }reverse_iterator rbegin()const { return _rbt.rbegin(); }reverse_iterator rend()const { return _rbt.rend(); }public:// 构造set(){}set(const set& st) {_rbt = st._rbt;}set(std::initializer_list<Key> init_list) {for (const Key& key : init_list) {insert(key);}}//迭代器构造template<class input_iter>set(input_iter begin, input_iter end) {while (begin != end) {insert(*(begin++));}}public:iterator find(const Key& key)const {return _rbt.find(key);}pair<iterator,bool> insert(const Key& key) {pair<typename RBTree::iterator, bool> res = _rbt.insert_unique(key);return make_pair(iterator(res.first), res.second);}size_t erase(const Key& key) {return _rbt.erase(key);}void clear() { _rbt.clear(); }bool empty() { return _rbt.empty(); }size_t size() { return _rbt.size(); }bool valid_RBTree() { return _rbt.is_RBTree(); }};
}

2，multiset

namespace mySTL {// multisettemplate<class Key, class Compare = less<Key>>class multiset {private:struct KeyOfVal {const Key& operator()(const Key& key) { return key; }};typedef RBTree<Key, Key, KeyOfVal, Compare> RBTree;RBTree _rbt;public:// 迭代器typedef typename RBTree::const_iterator			iterator;typedef typename RBTree::const_iterator			const_iterator;typedef typename RBTree::const_reverse_iterator reverse_iterator;typedef typename RBTree::const_reverse_iterator const_reverse_iterator;iterator begin()const { return _rbt.begin(); }iterator end()const { return _rbt.end(); }reverse_iterator rbegin()const { return _rbt.rbegin(); }reverse_iterator rend()const { return _rbt.rend(); }public:// 构造multiset() {}multiset(const multiset& st) {_rbt = st._rbt;}multiset(std::initializer_list<Key> init_list) {for (const Key& key : init_list) {insert(key);}}//迭代器构造template<class input_iter>multiset(input_iter begin, input_iter end) {while (begin != end) {insert(*(begin++));}}public:iterator find(const Key& key)const {return _rbt.find(key);}iterator insert(const Key& key) {return _rbt.insert_equal(key);}size_t erase(const Key& key) {return _rbt.erase(key);}void clear() { _rbt.clear(); }bool empty() { return _rbt.empty(); }size_t size() { return _rbt.size(); }bool valid_RBTree() { return _rbt.is_RBTree(); }};
}

set 与 multiset 在实现中其实没什么区别，就只是插入的方式不同（一个用 insert_unique，另一个用 insert_equal）

三，map 与 multimap 的实现

map、multimap 也会根据元素的键值自动进行排序，这两个容器中的元素都是 pair<key, val> 键值对。map 不允许两个元素有相同的键，multimap 允许出现重复的键。map、multimap 不允许修改键值，但是可以修改实值（不能修改 key，可以修改 val），因为容器中元素的排列规则是依靠 key 来比较，val 并不会影响这个规则。

1，map

namespace mySTL {// maptemplate<class Key, class Val, class Compare = less<Key>>class map {struct KeyOfVal {Key operator()(const pair<const Key, Val>& p) {return p.first;}};typedef RBTree<Key, pair<const Key, Val>, KeyOfVal, Compare> RBTree;RBTree _rbt;public:// 迭代器typedef typename RBTree::iterator				iterator;typedef typename RBTree::const_iterator			const_iterator;typedef typename RBTree::reverse_iterator		reverse_iterator;typedef typename RBTree::const_reverse_iterator const_reverse_iterator;iterator begin() { return _rbt.begin(); }iterator end() { return _rbt.end(); }const_iterator begin() const { return _rbt.begin(); }const_iterator end() const { return _rbt.end(); }reverse_iterator rbegin() { return _rbt.rbegin(); }reverse_iterator rend() { return _rbt.rend(); }const_reverse_iterator rbegin()const { return _rbt.rbegin(); }const_reverse_iterator rend()const { return _rbt.rend(); }public:// 构造map() {}map(const map& mp) {_rbt = mp._rbt;}map(std::initializer_list<pair<Key, Val>> init_list) {for (const pair<Key, Val>& data : init_list) {insert(data.first, data.second);}}//迭代器构造template<class input_iter>map(input_iter begin, input_iter end) {while (begin != end) {insert(begin->first, begin->second);++begin;}}public:pair<iterator, bool> insert(const Key& key,const Val& val) {pair<iterator, bool> res = _rbt.insert_unique(make_pair(key, val));return res;}size_t erase(const Key& key) { return _rbt.erase(key); }iterator find(const Key& key) {return _rbt.find(key);}Val& operator[](const Key& key) {return insert(key, Val()).first->second;}bool empty() { return _rbt.empty(); }size_t size() { return _rbt.size(); }bool valid_RBTree() { return _rbt.is_RBTree(); }};
}

2，multimap

namespace mySTL {// multimaptemplate<class Key, class Val, class Compare = less<Key>>class multimap {struct KeyOfVal {Key operator()(const pair<const Key, Val>& p) {return p.first;}};typedef RBTree<Key, pair<const Key, Val>, KeyOfVal, Compare> RBTree;RBTree _rbt;public:// 迭代器typedef typename RBTree::iterator				iterator;typedef typename RBTree::const_iterator			const_iterator;typedef typename RBTree::reverse_iterator		reverse_iterator;typedef typename RBTree::const_reverse_iterator const_reverse_iterator;iterator begin() { return _rbt.begin(); }iterator end() { return _rbt.end(); }const_iterator begin() const { return _rbt.begin(); }const_iterator end() const { return _rbt.end(); }reverse_iterator rbegin() { return _rbt.rbegin(); }reverse_iterator rend() { return _rbt.rend(); }const_reverse_iterator rbegin()const { return _rbt.rbegin(); }const_reverse_iterator rend()const { return _rbt.rend(); }public:// 构造multimap() {}multimap(const multimap& mp) {_rbt = mp._rbt;}multimap(std::initializer_list<pair<Key, Val>> init_list) {for (const pair<Key, Val>& data : init_list) {insert(data.first, data.second);}}//迭代器构造template<class input_iter>multimap(input_iter begin, input_iter end) {while (begin != end) {insert(begin->first, begin->second);++begin;}}public:iterator insert(const Key& key, const Val& val) {return _rbt.insert_equal(make_pair(key, val));}size_t erase(const Key& key) { return _rbt.erase(key); }iterator find(const Key& key) {return _rbt.find(key);}bool empty() { return _rbt.empty(); }size_t size() { return _rbt.size(); }bool valid_RBTree() { return _rbt.is_RBTree(); }};
}

map 与 multimap 在实现上其实也没有多大的差别，主要的区别还是体现在插入的方式上