话不多说,直接看题:
1.

我们可以得到大致一个思路,就是先枚举1-1e6的质数,然后看看有几个即可。
我们怎么知道个数呢?
首先我们知道1---n中有n/p的下取整个为p的倍数。
因此,p的个数至少是n/p的下取整个,当然有些数有不止1个p的倍数,于是我们得到n/p^2+n/p^3+...直到p^i>n.
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1000010;
int pri[N],cnt;
bool st[N];
void getpri(int n){for(int i=2;i<=n;i++){if(!st[i]) pri[cnt++]=i;for(int j=0;pri[j]*i<=n;j++){st[pri[j]*i]=1;if(i%pri[j]==0) break;}}
}
int main(){int n;cin>>n;getpri(n);for(int i=0;i<cnt;i++){int p=pri[i];int s=0,t=n;while(t){s+=t/p;t/=p;}printf("%d %d\n",p,s);}
}2.

我们把数按照基本算数定理拆分,我们对于每一个质数的奇数,答案就乘这个,若为偶数,那么就不用管,下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int main(){LL n;cin>>n;LL res=1;for(LL i=2;i*i<=n;i++){if(n%i==0){int s=0;while(n%i==0){s++;n/=i;}if(s%2) res*=i;}}if(n>1) res*=n;cout<<res;
}3.

下面是分析:
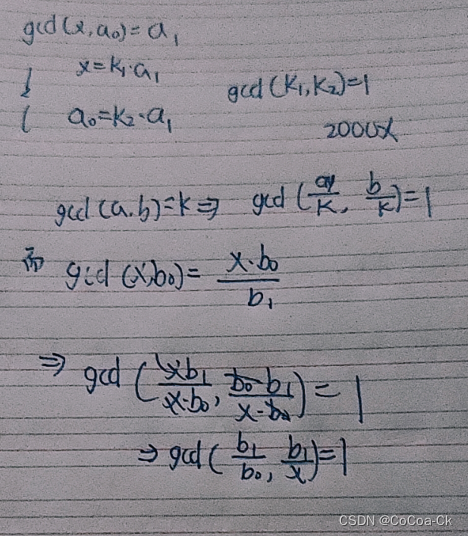
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int gcd(int a,int b){return b?gcd(b,a%b):a;
}
int T,a0,a1,b0,b1;
int ans;
int main(){cin>>T;while(T--){ans=0;scanf("%d%d%d%d",&a0,&a1,&b0,&b1);int p1=a0/a1,p2=b1/b0;for(int i=1;i*i<=b1;i++){if(b1%i) continue;if(i%a1==0&&gcd(i/a1,p1)==1&&gcd(b1/i,p2)==1) ans++;if(i==b1/i) continue;int ck=b1/i;if(ck%a1==0&&gcd(ck/a1,p1)==1&&gcd(b1/ck,p2)==1) ans++;}printf("%d\n",ans);}
}4.

这里主要介绍一个定理:求两个数的约数等价于最大公约数的因子,于是我们求出gcd,然后求约数即可,下面是AC代码:
#include<bits/stdc++.h>using namespace std;
int q[5000],cnt;
int gcd(int a,int b){return b?gcd(b,a%b):a;
}
int main(){int a,b;cin>>a>>b;int d=gcd(a,b);for(int i=1;i<=d/i;i++){if(d%i==0){q[cnt++]=i;if(i!=d/i) q[cnt++]=d/i;}}sort(q,q+cnt);int n;cin>>n;while(n--){int L,R;scanf("%d%d",&L,&R);int f=0;for(int i=cnt-1;i>=0;i--){if(q[i]>=L&&q[i]<=R){printf("%d\n",q[i]);f=1;break;}}if(f==0) cout<<-1<<endl;}
}

)








)







