【数据结构】树与森林（树的存储结构、森林与二叉树的转化、树与森林的遍历）

树和森林
- 树的存储结构
- - 一、树的双亲表示法：
  - 二、树的孩子表示法
  - - 方法一：定长结点的多重链表
    - 方法二：不定长结点的多重链表
    - 方法三：孩子单链表表示法
  - 三、树的二叉链表(孩子-兄弟)存储表示法
- 森林与二叉树的转换
- 树和森林的遍历
- - 先根(次序)遍历
  - 后根(次序)遍历（待补充）
  - 按层次遍历(待补充）

树与二叉树知识点文章: 【数据结构】树与二叉树（递归法先序、中序、后序、层次遍历二叉树、二叉树的建立以及求树高的方法）
二叉树遍历算法的应用: 【数据结构】树与二叉树遍历算法的应用（求叶子节点个数、求树高、复制二叉树、创建二叉树、二叉树存放表达式、交换二叉树每个结点的左右孩子）

树和森林

树的非顺序存储映像：

双亲表示法
孩子表示法
树的二叉链表(孩子-兄弟)存储表示法

树的存储结构

一、树的双亲表示法：

祖先（双亲）
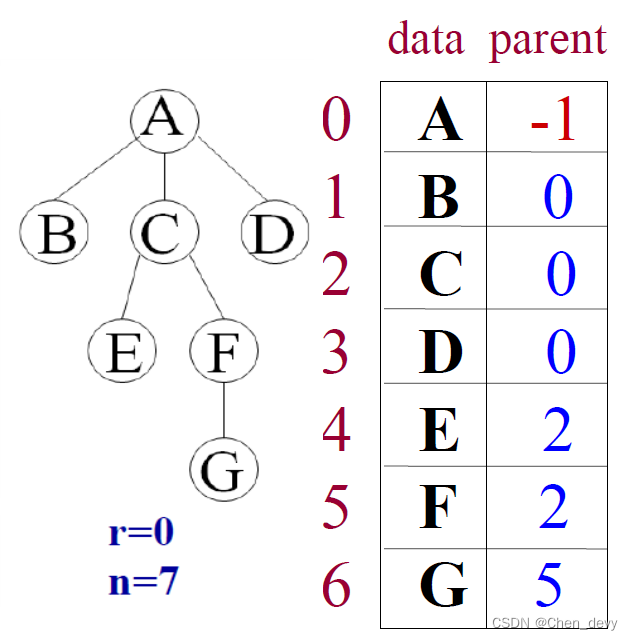
定义：用一维数组存放树中的每一结点的值(data)和双亲位置（parent,逻辑关系）

特点：找祖先易，找子孙难
典型用例：并查集
在这里插入图片描述

//树的双亲表示法
#define MAX_TREE_SIZE 100
typedef struct PTNode {int data;int parent;  // 双亲位置
} PTNode;typedef struct {PTNode nodes[MAX_TREE_SIZE];int  r,n;//r为根节点的位置,n为树中结点的个数
} PTree;

说明：结点存放无顺序要求，根结点不一定存在第一个位置；每个数组元素对应树中一个结点，存放结点的值和双亲位置r—根结点位置，n—树中结点个数。

二、树的孩子表示法

树的孩子表示法:存放树中每个结点的信息、直接后继的地址。

根据结点直接后继的存放方式，分为：

定长结点的多重链表：每个结点按照树的度设置孩子指针的数量
不定长结点的多重链表：每个结点按照结点自身的度设置孩子指针的数量
孩子单链表：每个结点的孩子结点（直接后继）建一个单链表

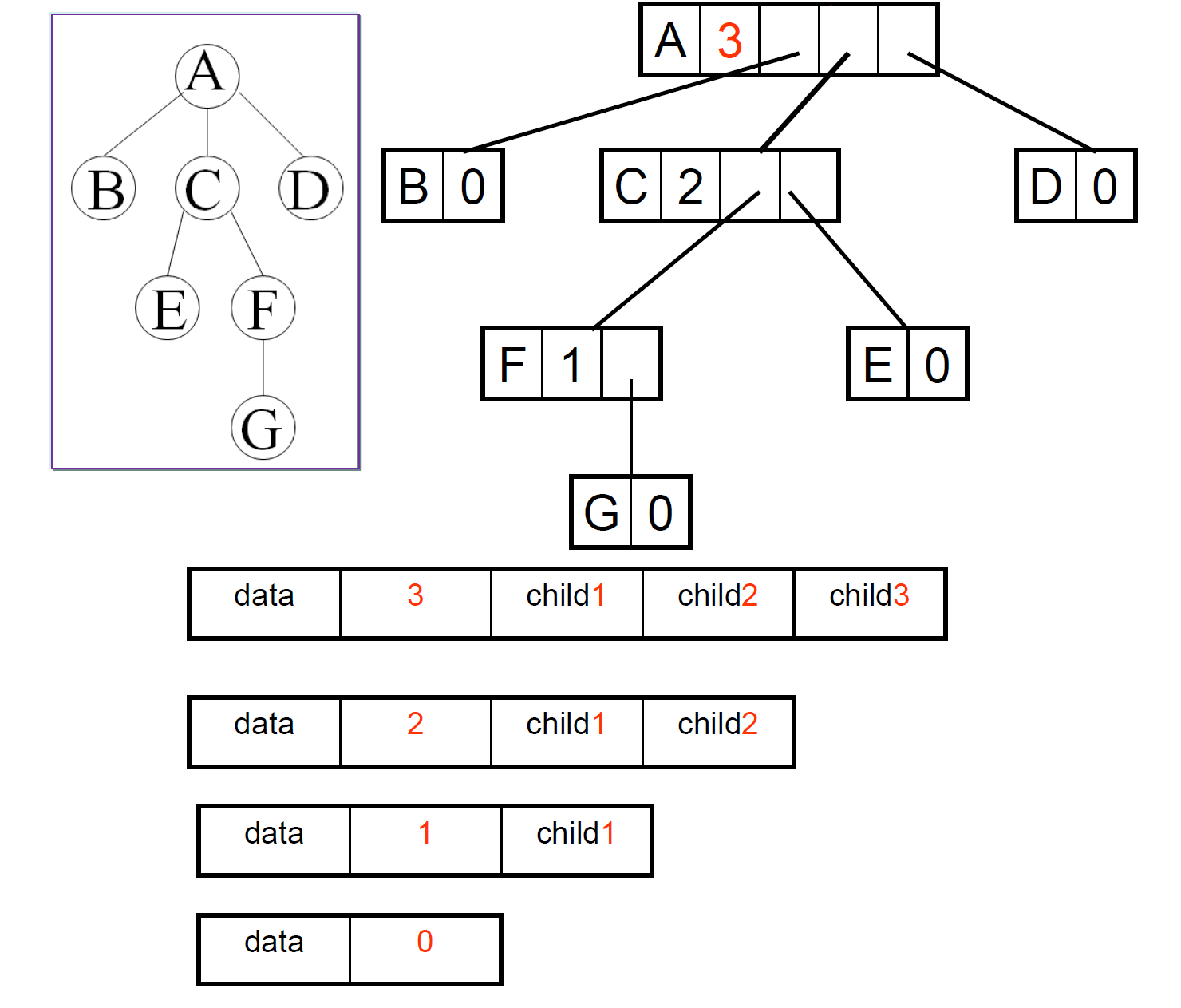
方法一：定长结点的多重链表

树的孩子表示法：定长结点的多重链表
(典型：实现树的层次遍历)

定义：链表存放树中的每一结点的值(data)和孩子结点位置(child[i]，第i个孩子指针，表示逻辑关系)，每个结点的孩子指针的个数=树中孩子最多的结点的孩子个数=树的度.
在这里插入图片描述

1. 特点：结点的结构统一，若树的度为d，则点包含一个数据域，d个孩子指针域.

2. 缺点：空指针多，浪费空间

方法二：不定长结点的多重链表

树的孩子表示法–不定长结点的多重链表

定义：链表存放树中的每一结点的值(data)和孩子结点位置（child[i]，逻辑关系），每个结点的孩子指针的个数=该结点的孩子个数=结点的度
在这里插入图片描述

树的度为d,该树的不定长结点的多重链表中结点结构有几种？
树的度为d=3,该树的不定长结点的多重链表中结点结构有4种
总结：树的度为d,该树的不定长结点的多重链表中结点结构有d+1种.

特点：结点的结构不统一，包含一个数据域，结点的度d， d个孩子指针域
缺点：操作较复杂

方法三：孩子单链表表示法

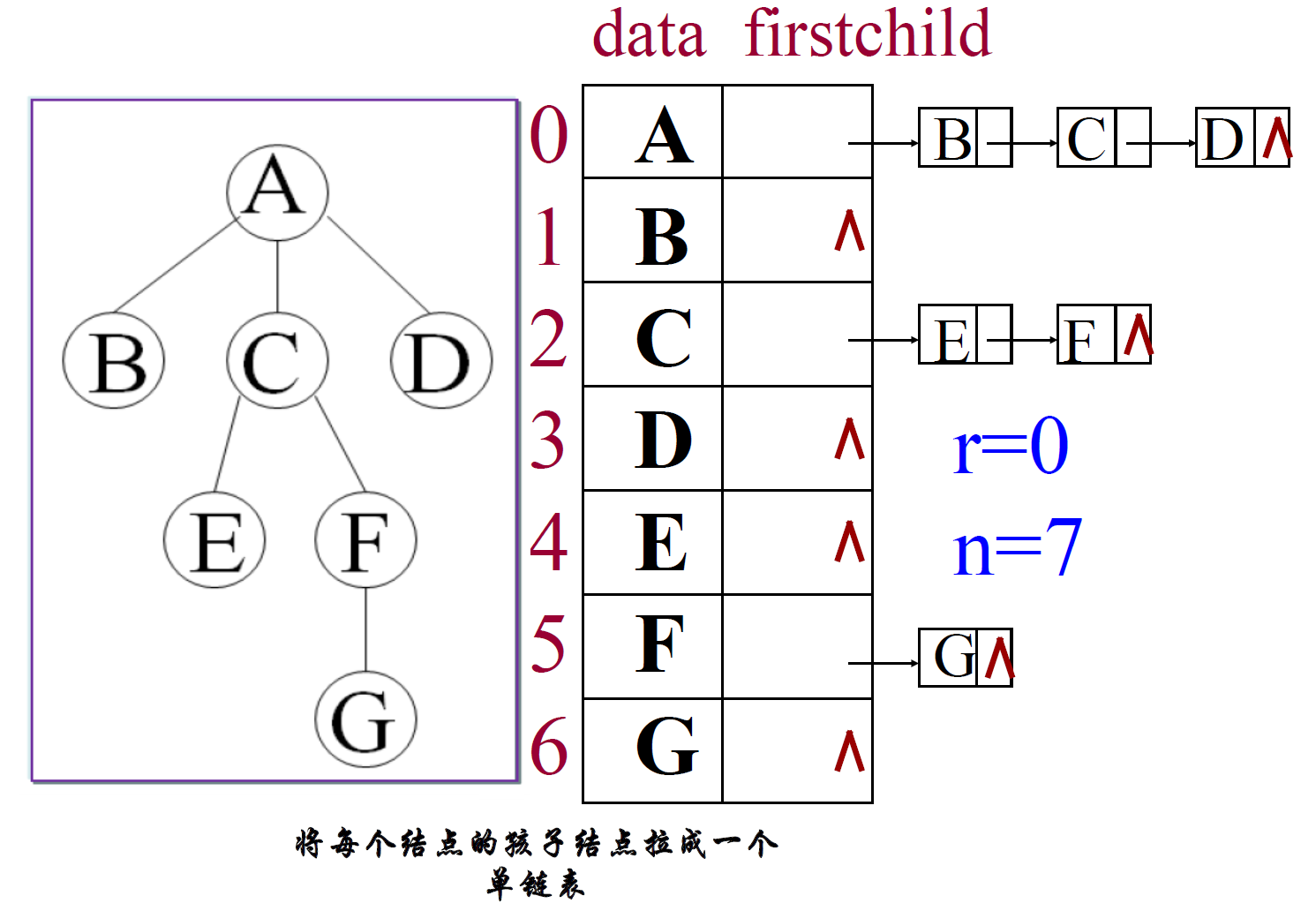
将每个结点的孩子结点拉成一个单链表
情况一：
结点C在孩子表示法中存了2次：
一次出现在下标为2的数组元素中，该数组元素同时保存了C的孩子单链表的头指针。
一次出现在结点A的孩子单链表中。
数据元素存放多次，更新操作比较麻烦，更新一个数据元素，所有保存该数据元素的地方均要更新，否则信息不一致！

在这里插入图片描述

情况二：
为节省存储空间、方便更新操作和数据维护，每个数据元素只在数组中存放一次；
在孩子单链表中只存放这个孩子在数组中的位置。
如下图所示：
结点A的孩子单链表中第一个孩子结点是下标为1的数组元素（B），第二个孩子是下标为2的数组元素（C），第三个孩子是下标为3的数组元素（D）。
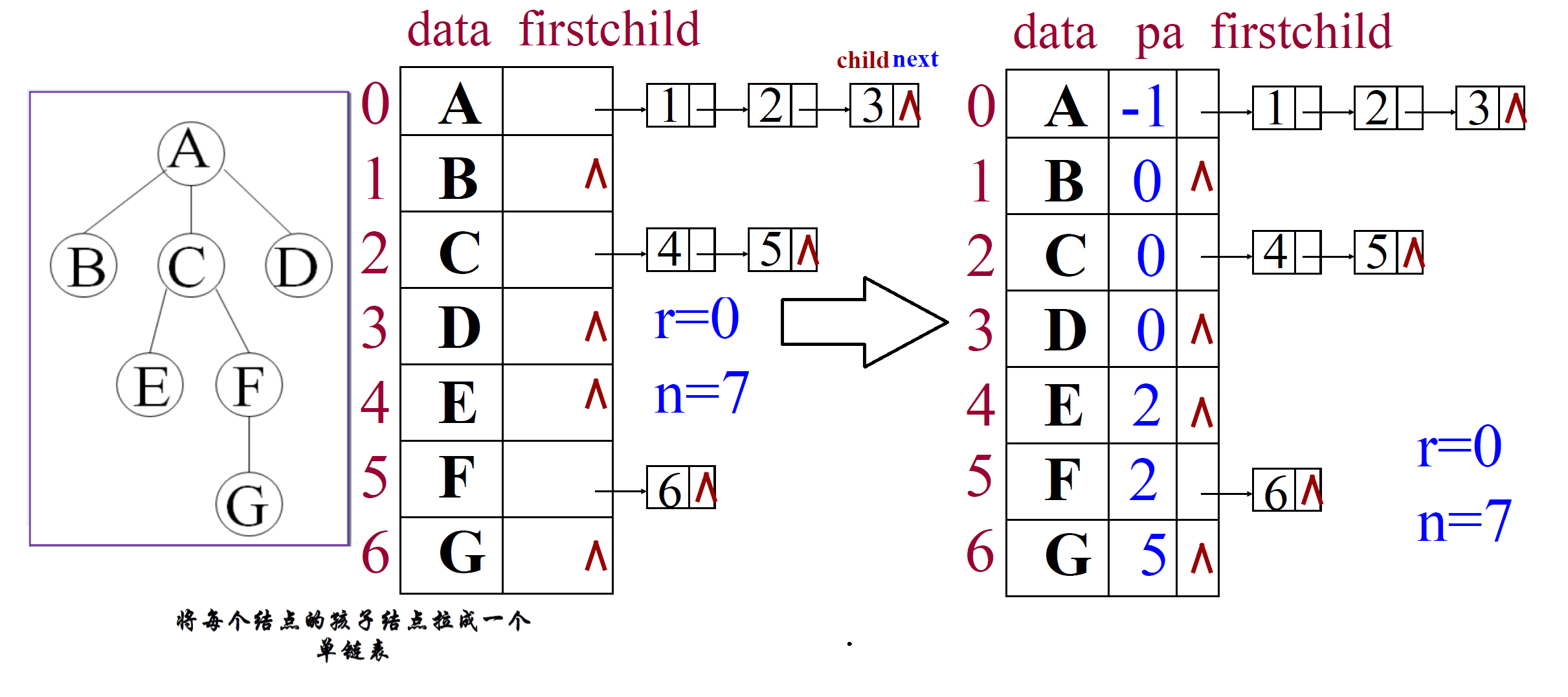
在这里插入图片描述

若既要找子孙，又要找祖先，可将孩子单链表和双亲表示法结合在一起每个数组元素的data域存放数据元素的值，pa域存放双亲结点在数组中的位置，firstchild存其孩子单链表的头指针。

typedef struct CTNode{ int child;struct CTNode *next;} *ChildPtr;//数组元素类型：
typedef struct{ ElemType  data; ChildPtr firstchild;
//孩子单链表的头指针
} CTBox;//树：
typedef struct{CTBox nodes[MAX_TREE_SIZE]; int  n,r;
// 树的结点数和根结点的位置
} CTree;

三、树的二叉链表(孩子-兄弟)存储表示法

[fc,data,nb]
在这里插入图片描述

typedef structCSNode{ElemType data;structCSNode*fc, *nb;
}CSNode, *CSTree;

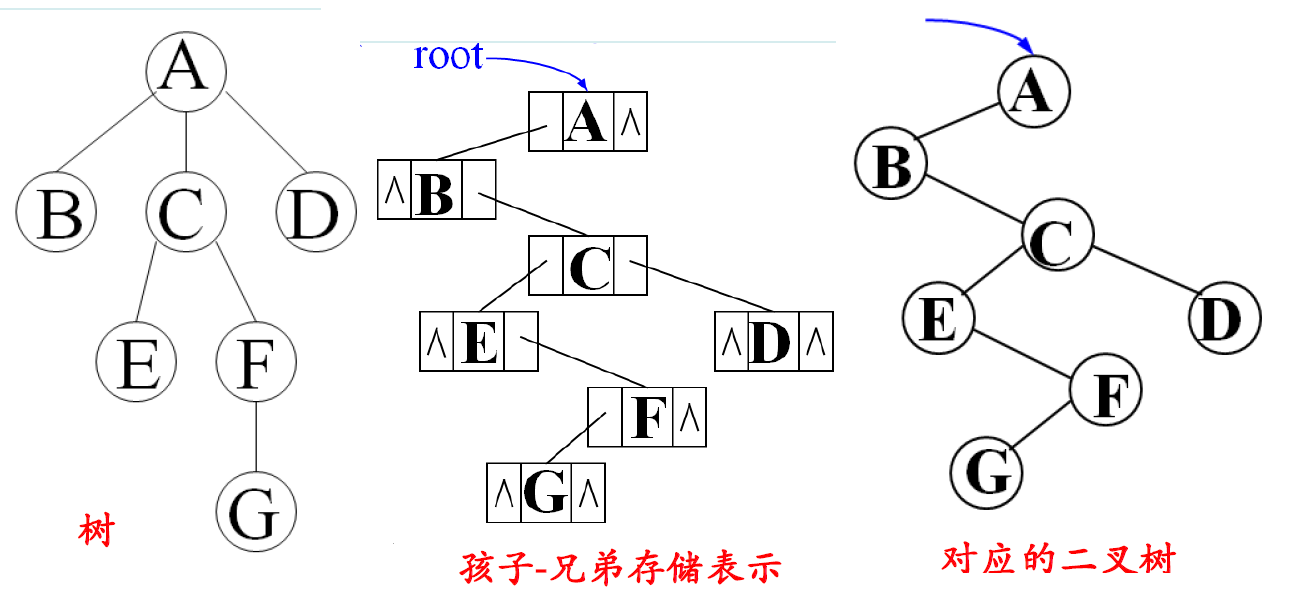
树中每个结点三部分：
数据域（data），长子指针域(fc)，
右邻兄弟指针域(nb)

树和二叉树的转换
• 树以孩子兄弟表示法存，相当于将树转换成二叉树，但此二叉树根结点无右子树
• 好处：借助二叉树的操作实现树的操作

森林与二叉树的转换

⮚ 树采用二叉链表(孩子-兄弟)存储表示法，转换成二叉树
⮚ 森林由多棵树组成： $F = (T 1, T 2, \dots, T n)$ ; 将其每棵树转换成二叉树 $B T_{1}, B T_{2}, \dots, BT n$ ;
⮚ 每棵二叉树BT的根的右子树皆为空树，从BTn开始依次将其根结点链为前一棵二叉树的根的右孩子
⮚ 将森林转换成一棵二叉树，森林的操作可借助二叉树的操作完成

森林和二叉树的转换
• 森林以孩子兄弟表示法存，相当于将森林转换成二叉树
• 好处：借助二叉树的操作实现森林的操作

树和森林的遍历

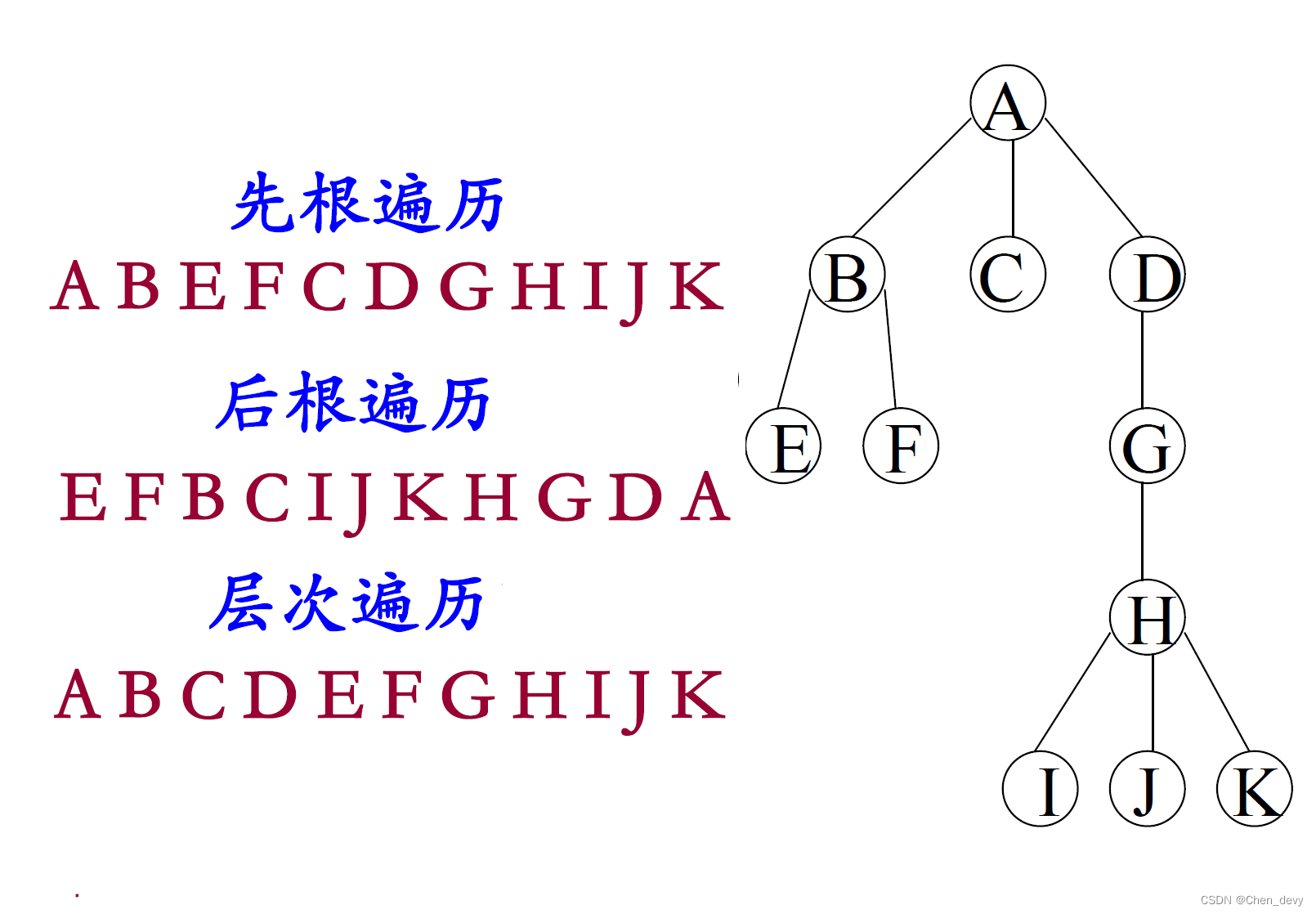
■ 树的遍历可有三条搜索路径:
⮚ 先根(次序)遍历:若树不空，则先访问根结点，然后依次先根遍历各棵子树。
⮚ 后根(次序)遍历:若树不空，则先依次后根遍历各棵子树，然后访问根结点。
⮚ 按层次遍历:若树不空，则自上而下自左至右访问树中每个结点。
在这里插入图片描述

[fc,data,nb]

typedef structCSNode{int data;structCSNode*fc, *nb;
}CSNode, *CSTree;

树中每个结点三部分：数据域（data），长子指针域(fc)，右邻兄弟指针域(nb)

先根(次序)遍历

对应二叉树的先序

//树的孩子兄弟表示法
typedef structCSNode{ElemType data;structCSNode*fc, *nb;
}CSNode, *CSTree;//二叉树的二叉链表表示法
typedef struct BiTNode {ElemType  data;struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;void PreorderTraverse(CSTree T){SeqStack s ;	s.top=-1; p = T;while(p){while(p){printf(“%c”,p->data);if(p->nb)if(s.top==MAX-1) exit (0);else s.data[++s.top]=p->nb;p =p->fc;}if (s.top!=-1) p=s.data[s.top--];}
}