📃博客主页： 小镇敲码人
🚀 欢迎关注：👍点赞 👂🏽留言 😍收藏
🌏 任尔江湖满血骨，我自踏雪寻梅香。 万千浮云遮碧月，独傲天下百坚强。 男儿应有龙腾志，盖世一意转洪荒。 莫使此生无痕度，终归人间一捧黄。🍎🍎🍎
❤️ 什么？你问我答案，少年你看，下一个十年又来了 💞 💞 💞

前言：本篇博客旨在帮助大家学习和了解DP算法，并熟练的掌握DP算法的原理和一些套路，以题解的形式给出，题目出自力扣平台，后面的数字代表难度分。

OJ题1：石子游戏,难度分:1590

这里是题目链接

题目解析

算法原理

下面我们来尝试使用动态规划来解决这道题。

代码实现

class Solution {
public:bool stoneGame(vector<int>& piles) {//创建dp表//初始化//填表//返回值int n = piles.size();vector<vector<int>> dp(n,vector<int>(n));dp[0][0] = piles[0];dp[n-1][n-1] = piles[n-1];for(int i = n-2;i >= 0;i--)for(int j = i;j < n;j++)if(j > 0)dp[i][j] = max(piles[i]-dp[i+1][j],piles[j]-dp[i][j-1]);return dp[0][n-1] > 0;}
};

ak截图：

使用滚动数组优化

代码实现：

class Solution {
public:bool stoneGame(vector<int>& piles) {//创建dp表//初始化//填表//返回值int n = piles.size();vector<int> dp(n);dp[0] = piles[0];dp[n-1] = piles[n-1];for(int i = n-2;i >= 0;i--)for(int j = i;j < n;j++)if(j > 0)dp[j] = max(piles[i]-dp[j],piles[j]-dp[j-1]);return dp[n-1] > 0;}
};

ak截图：

OJ题2：下降路径最小和 难度分:1573

这里是题目链接

题目解析

算法原理

我们尝试使用动态规划来解决一下这道题

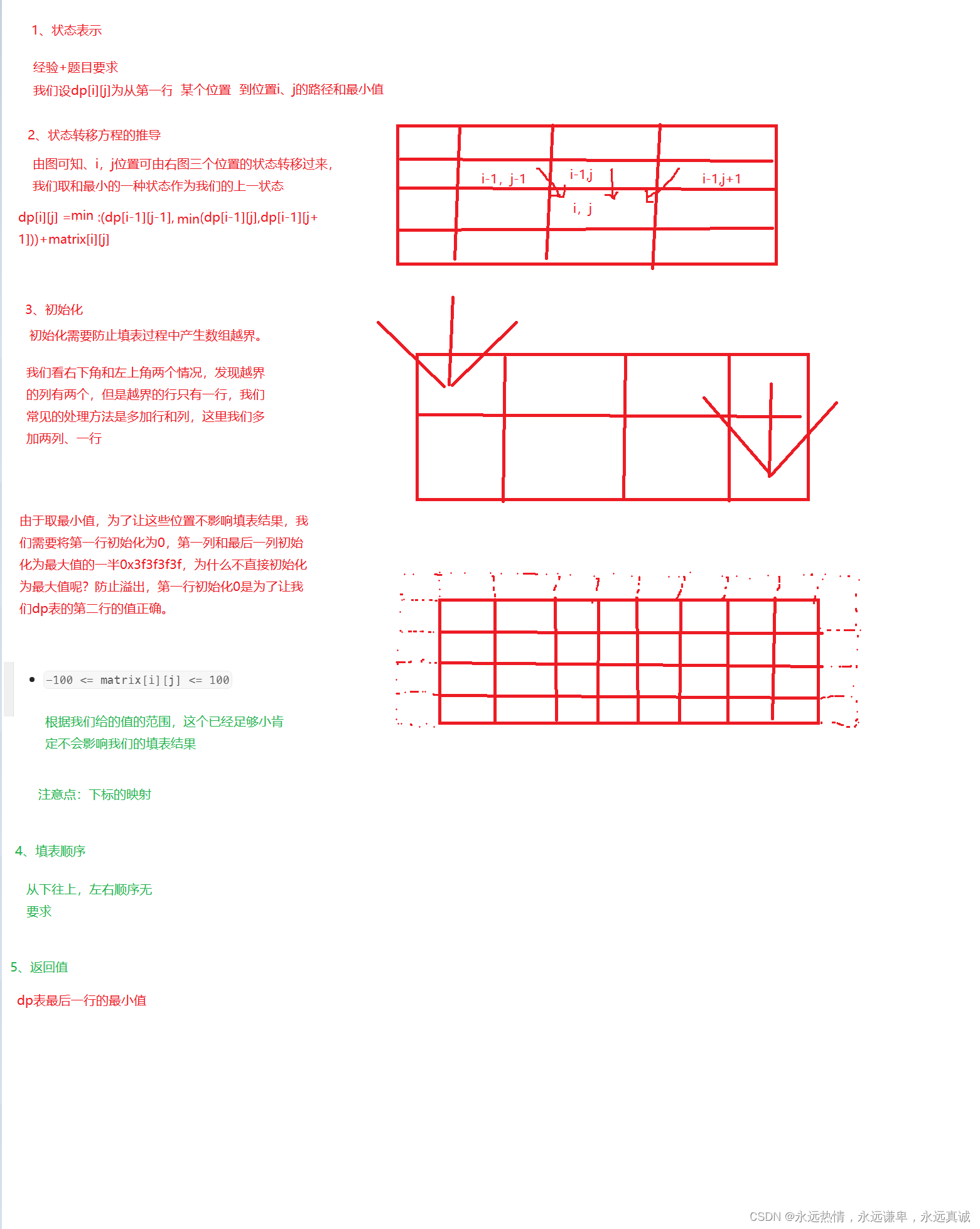
代码实现

class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {//创建dp表//初始化//填表//返回值int INF = 0x3f3f3f3f;int n = matrix.size();int m = matrix[0].size();vector<vector<int>> dp(n+1,vector<int>(m+2,INF));for(int j = 0;j <= m;++j)dp[0][j] = 0;for(int i = 1;i <= n;++i)for(int j = 1;j <= m;++j)dp[i][j] = min(dp[i-1][j-1],min(dp[i-1][j],dp[i-1][j+1]))+matrix[i-1][j-1];int ret = INF;for(int j = 1;j <= m;++j)ret = min(ret,dp[n][j]);return ret;}
};

ak截图：

OJ题3：最长字符串链 难度分:1599

这里是题目链接

题目解析

算法原理

下面我们使用动态规划来解决一下这道题。

代码实现

int compare(string& a,string& b)
{return a.size() < b.size();
}
class Solution {
public:int longestStrChain(vector<string>& words) {sort(words.begin(),words.end(),compare);//排序unordered_map<string,int> hash;int n = words.size();for(int i = 0;i < n;++i)hash[words[i]] = i;vector<int> dp(n,1);int ret = 1;for(int i = 1;i < n;++i){for(int j = 0;j < words[i].size();++j){string wordprev = words[i].substr(0,j)+words[i].substr(j+1);if(hash.count(wordprev))dp[i] = max(dp[hash[wordprev]]+1,dp[i]);}ret = max(ret,dp[i]);}return ret;}
};

ak截图：

OJ题4：最长定差子序列 难度分:1597

这里是题目链接

题目解析

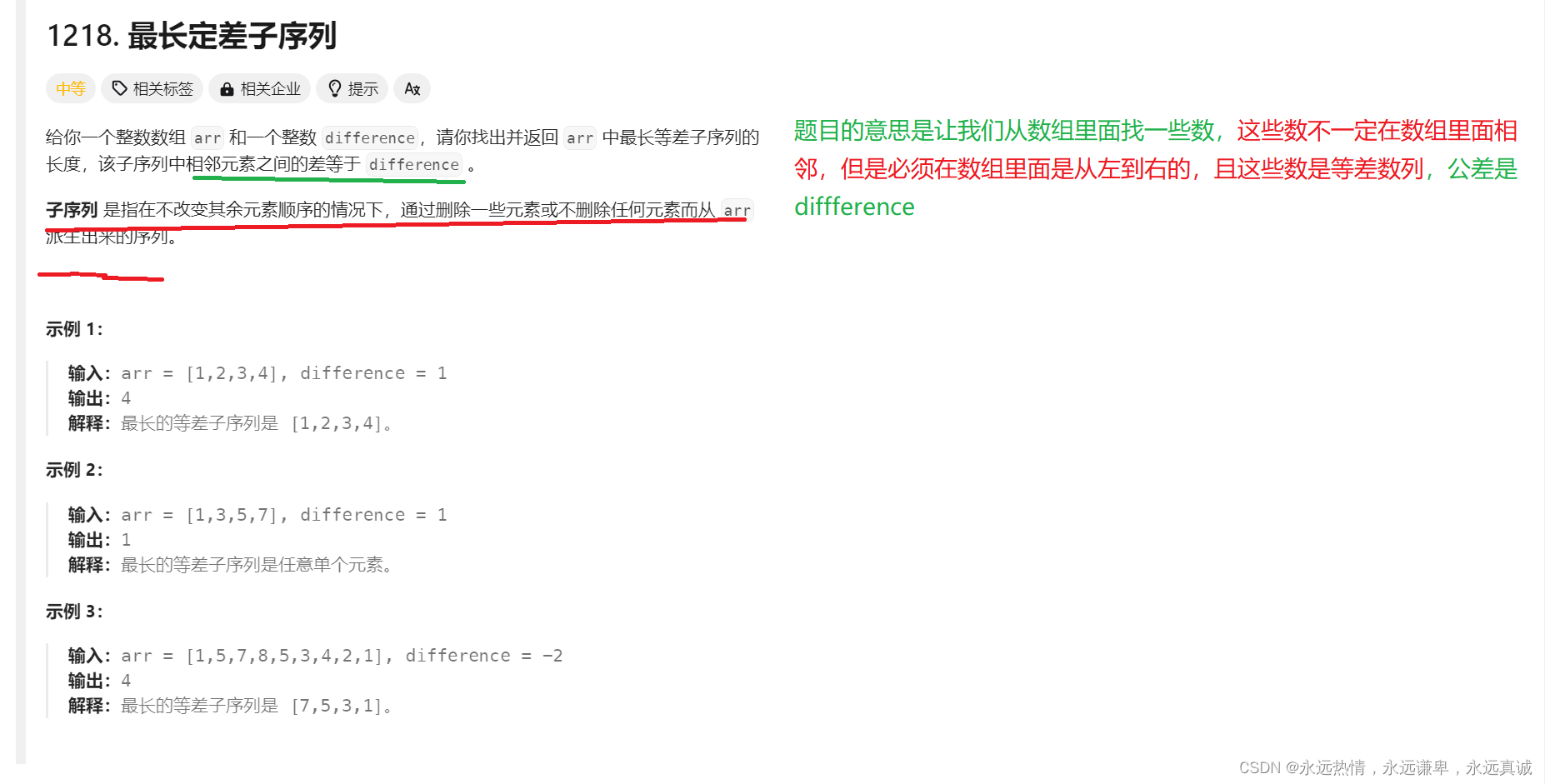
算法原理

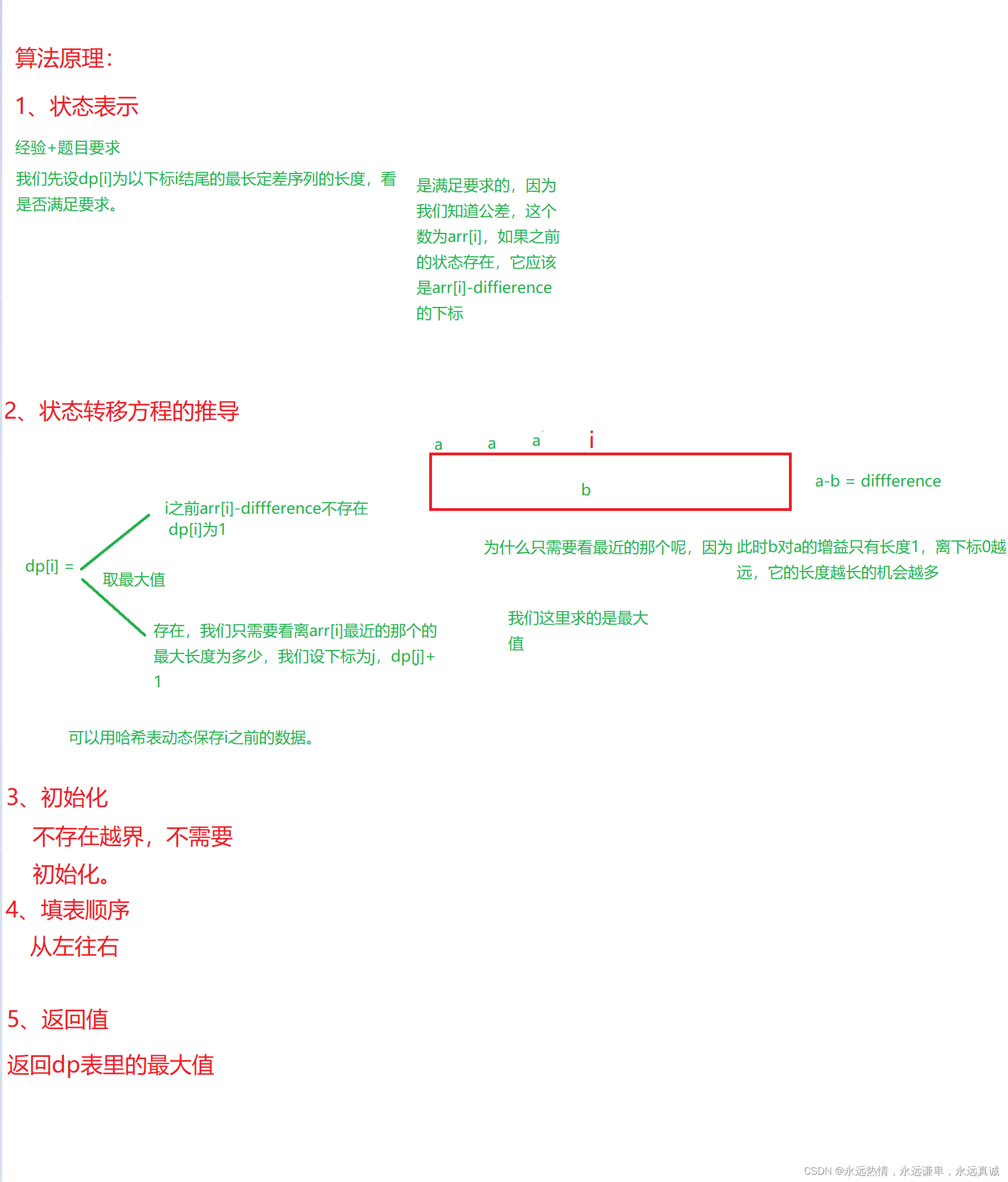
代码实现

class Solution {
public:int longestSubsequence(vector<int>& arr, int difference) {int n = arr.size();unordered_map<int,int> hash;//值-下标//创建dp表//初始化//填表//返回值vector<int> dp(n,1);int ret = 0;for(int i = 0;i < n;++i){int a = arr[i];if(hash.count(a-difference))dp[i] = dp[hash[a-difference]]+1;hash[arr[i]] = i;ret = max(ret,dp[i]);}return ret;}
};

ak截图：

OJ题5：将整数按权重排序 难度分:1507

这里是题目

题目解析

算法原理

代码实现

int compare(vector<int>& a,vector<int>& b)
{return a[1] < b[1] || (a[1] == b[1] && a[0] < b[0]);
}
class Solution {
private:unordered_map<int,int> dp;
public:int getF(int i){if(dp.count(i))return dp[i];if(i == 1)return 0;else if(i & 1)return dp[i] = 1+getF(3*i+1);elsereturn dp[i] = 1+getF(i/2);}int getKth(int lo, int hi, int k) {//创建dp表//初始化//填表vector<vector<int>> x;for(int i = lo;i <= hi;++i)x.push_back({i,getF(i)});sort(x.begin(),x.end(),compare);return x[k-1][0];}
};

ak截图：

OJ题6：使绳子变成彩色的最短时间 难度分:1574

使绳子变成彩色的最短时间

题目解析

算法原理

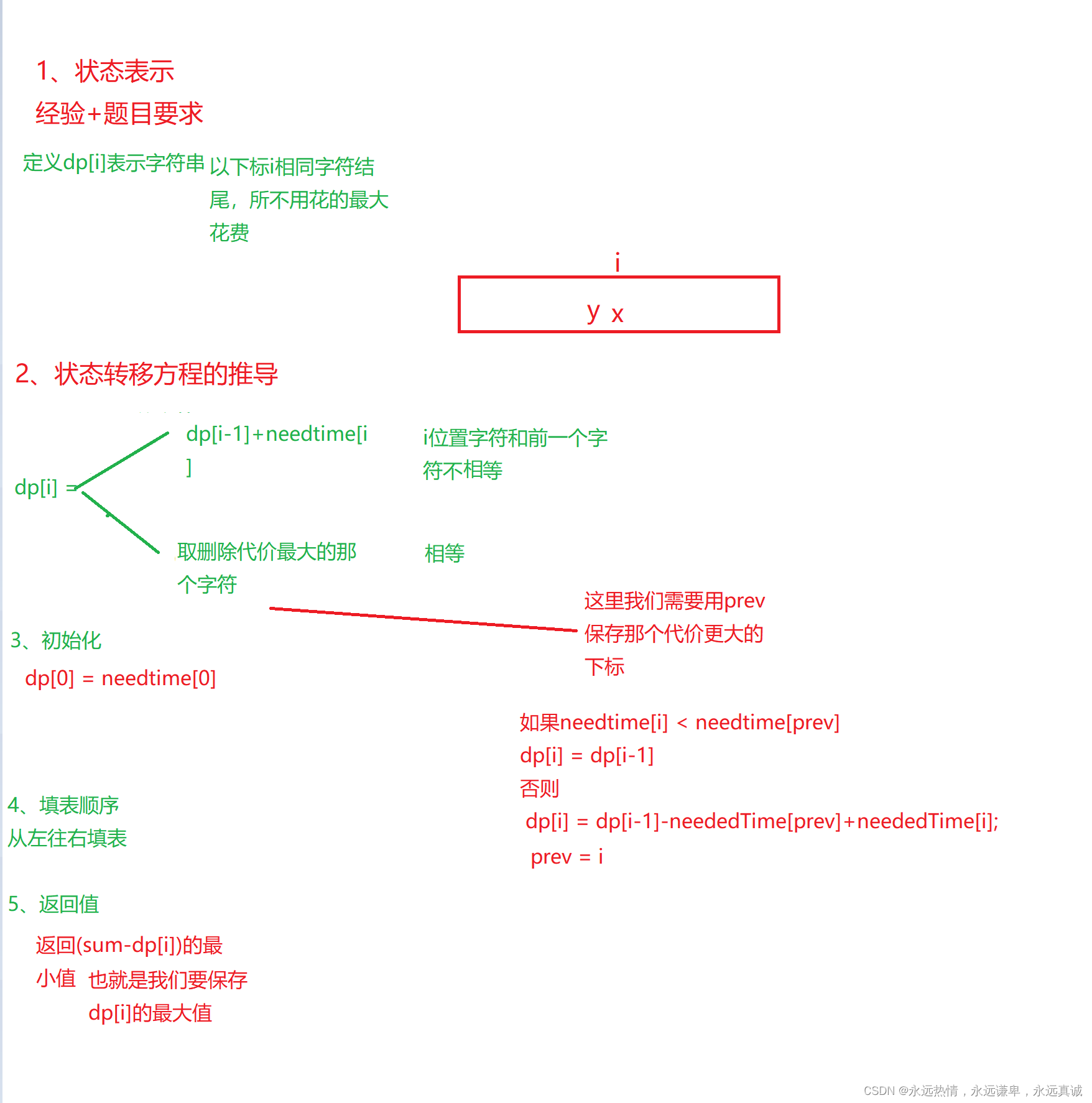
代码实现

class Solution {
public:int minCost(string colors, vector<int>& neededTime) {//创建dp表//初始化//填表//返回值int n = neededTime.size();vector<int> dp(n);int sum = 0;for(auto& i:neededTime)sum += i;dp[0] = neededTime[0];int ret = dp[0];int prev = 0;for(int i = 1;i < n;++i){if(colors[i] != colors[i-1]){dp[i] = dp[i-1]+neededTime[i];prev = i;}else {if(neededTime[i] > neededTime[prev]){dp[i] = dp[i-1]-neededTime[prev]+neededTime[i];prev = i;}elsedp[i] = dp[i-1];}ret = max(ret,dp[i]);}return sum-ret;}
};

ak截图：

OJ题7：统计字典序元音字符串的数目 难度分:1519

这里是题目

题目解析

算法原理

下面我们使用动态规划来解决一下这道题。

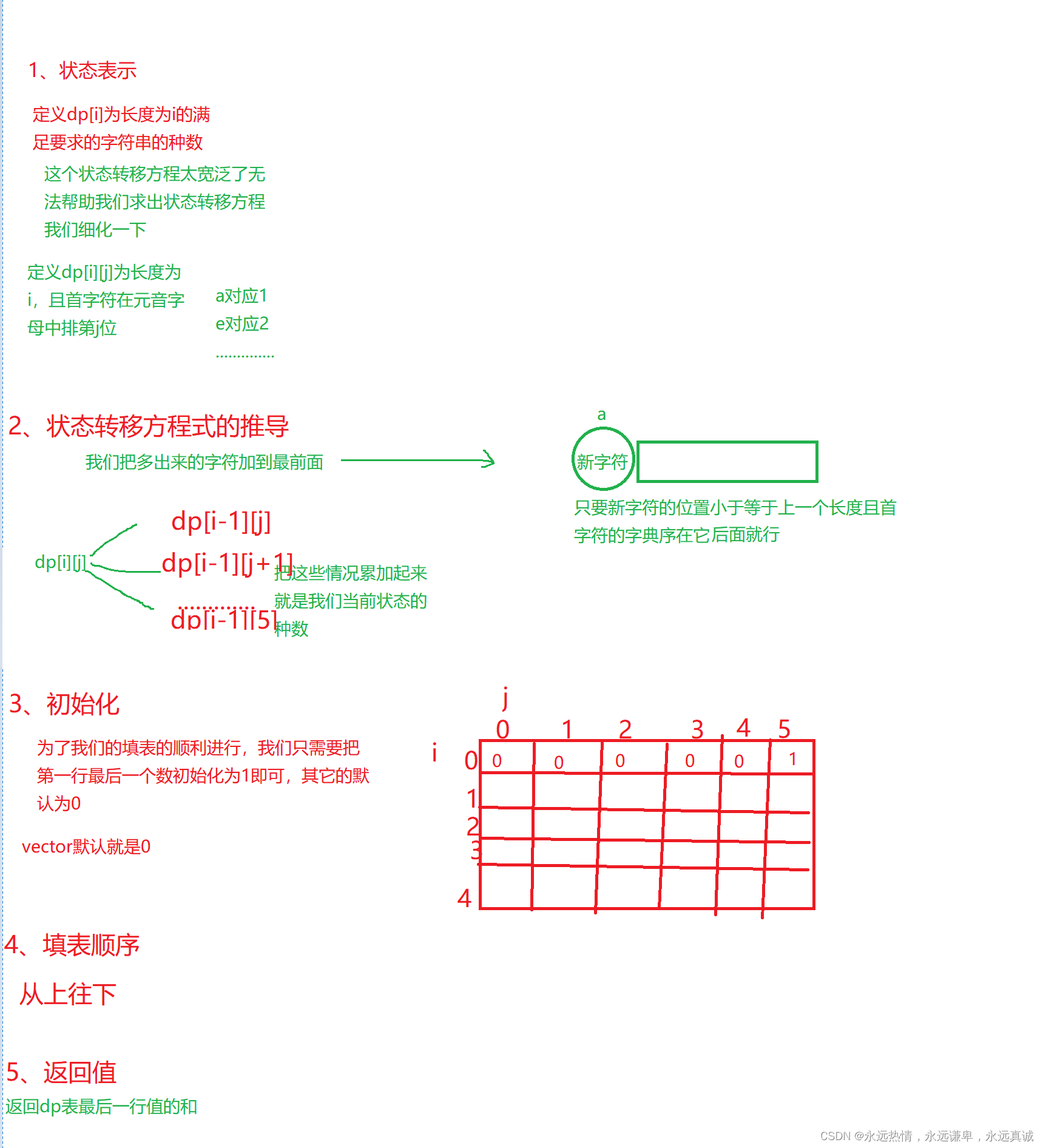
代码实现

class Solution {
public:int countVowelStrings(int n) {//创建dp表//初始化//填表//返回值vector<vector<int>> dp(n+1,vector<int>(6));dp[0][5] = 1;for(int i = 1;i <= n;++i)for(int j = 1;j <= 5;++j){for(int k = j;k <= 5;++k)dp[i][j] += dp[i-1][k];}int ret = 0;for(int i = 1;i <= 5;++i)ret += dp[n][i];return ret;}
};

ak截图：

滚动数组优化

很明显，每一个状态只依赖于它自己和它上一行后面列的数，只用一维数组实现滚动就可以了，注意要从左向右滚动，否则我们要的数就会被覆盖。

代码实现：

class Solution {
public:int countVowelStrings(int n) {//创建dp表//初始化//填表//返回值vector<int> dp(6);dp[5] = 1;for(int i = 1;i <= n;++i)for(int j = 1;j <= 5;++j){for(int k = j+1;k <= 5;++k)dp[j] += dp[k];}int ret = 0;for(int i = 1;i <= 5;++i)ret += dp[i];return ret;}
};

ak截图：

OJ题8：子数组和的绝对值的最大值 难度分:1542

这里是题目

题目解析

算法原理

下面我们使用动态规划来解决一下这道题。

代码实现

class Solution {
public:int maxAbsoluteSum(vector<int>& nums) {//创建dp表//初始化//填表//返回值int n = nums.size();vector<int> f(n),g(n);g[0] = f[0] = nums[0];int ret = abs(nums[0]);for(int i = 1;i < n;++i){f[i] = max(f[i-1]+nums[i],nums[i]);g[i] = min(g[i-1]+nums[i],nums[i]);ret = max(ret,max(f[i],abs(g[i])));}return ret;}
};

ak截图:

滚动数组优化

我们可以发现不管是g数组、还是f数组它每一次推导之前那个状态都只依赖于前一个状态，我们可以使用两个变量来取代那一个数组，不断让新的值覆盖这个变量即可，保证要用到上一个状态的时候它还没有被覆盖，所以要从左往右填表。

代码实现：

class Solution {
public:int maxAbsoluteSum(vector<int>& nums) {//创建dp表//初始化//填表//返回值int n = nums.size();int g = nums[0],f = nums[0];int ret = abs(nums[0]);for(int i = 1;i < n;++i){f = max(f+nums[i],nums[i]);g = min(g+nums[i],nums[i]);ret = max(ret,max(f,abs(g)));}return ret;}
};

ak截图：

OJ题9： 个位数字为 K 的整数之和 难度分:1559

这里是题目

题目解析

算法原理

代码实现

class Solution {
public:int minimumNumbers(int num, int k) {//创建dp表//初始化//返回值vector<int> dp(num+1,INT_MAX);vector<int> ans;//保存个位为k的数dp[0] = 0;for(int i = 1;i <= num;++i){if(i % 10 == k)dp[i] = 1;else{for(int j = 0;j < ans.size();++j){if(dp[i-ans[j]] != INT_MAX)dp[i] = min(dp[i],dp[i-ans[j]]+1);}}if(i % 10 == k)ans.push_back(i);}return dp[num] == INT_MAX ? -1:dp[num];}
};

ak截图：

OJ题10：达到末尾下标所需的最大跳跃次数 难度分:1533

这里是题目

题目解析

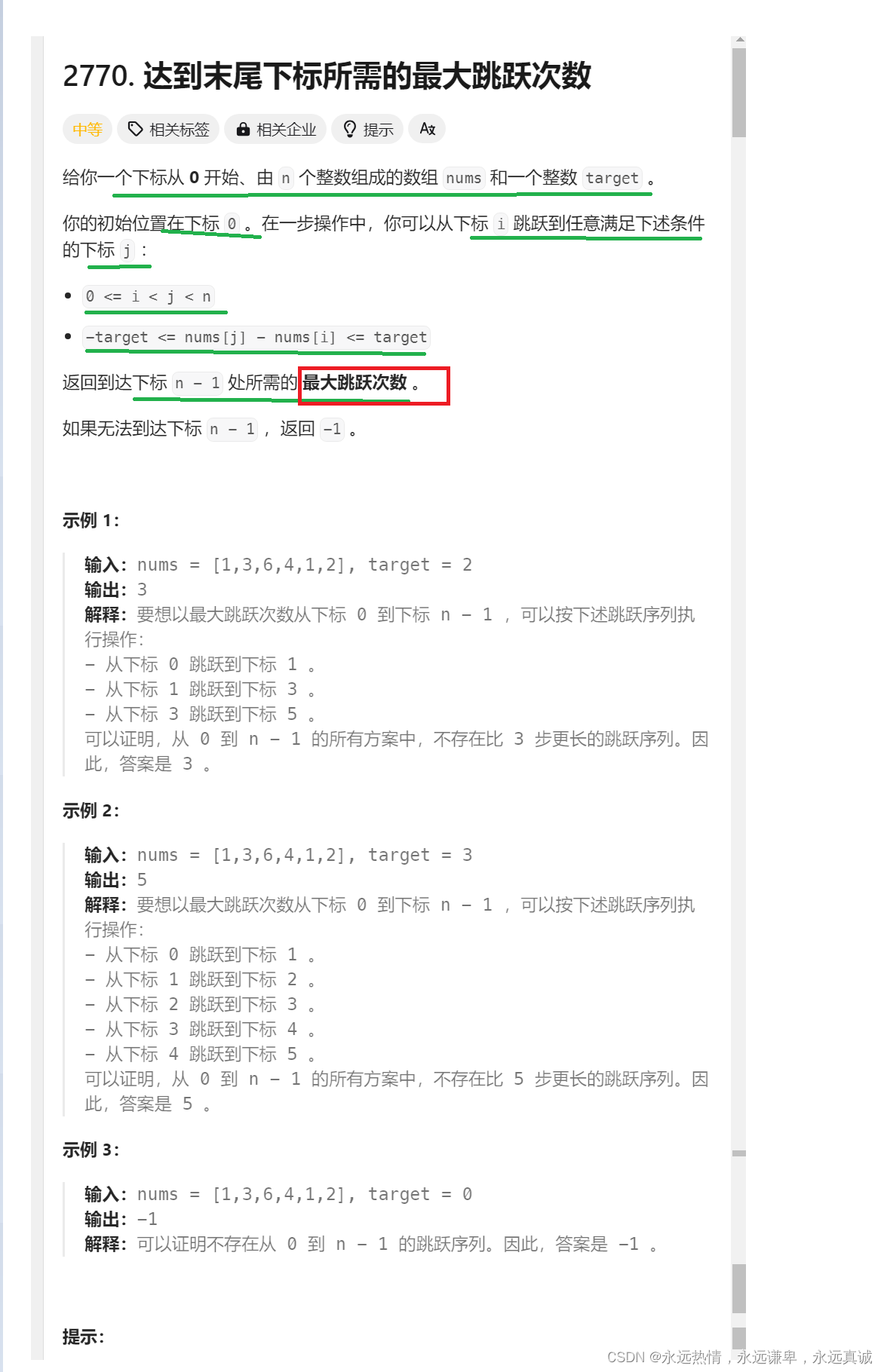
算法原理

我们来尝试使用动态规划来解决这个题目。

代码实现

class Solution {
public:int maximumJumps(vector<int>& nums, int target) {//创建dp表//初始化//返回值int n = nums.size();vector<int> dp(n,INT_MIN);dp[0] = 0;for(int i = 1;i < n;++i){for(int j = i-1;j >= 0;--j){int gap = abs(nums[j]-nums[i]);if(gap <= target && dp[j] != INT_MIN){dp[i] = max(dp[j]+1,dp[i]);}}}return dp[n-1] == INT_MIN ? -1 : dp[n-1];}
};

ak截图：

OJ题11：判断是否能拆分数组 难度分:1543 —区间dp

这里是题目

题目解析

算法原理

下面我们尝试使用动态规划来解决一下这道题。

代码实现

class Solution {
public:bool canSplitArray(vector<int>& nums, int m) {//创建dp表//初始化//返回值int n = nums.size();vector<vector<bool>> dp(n,vector<bool>(n,true));for(int i = 0;i+3 <= n;++i){if(nums[i]+nums[i+1] >= m || nums[i+1]+nums[i+2] >= m)dp[i][i+2] = true;elsedp[i][i+2] = false; }for(int i = n-2;i >= 0;--i){for(int j = i+3;j < n;++j)dp[i][j] = dp[i+1][j] || dp[i][j-1];}return dp[0][n-1];}
};

ak截图：

OJ题12：推多米诺 难度分：1638

这里是题目

题目解析

算法原理

下面我们使用动态规划来解决一下这道题。

代码实现

class Solution {
public:string pushDominoes(string& dominoes) {//创建dp表//初始化int n = dominoes.size();vector<int> dp(n,0);if(dominoes[0] == 'L')dp[0] = -1;if(dominoes[0] == 'R')dp[0] = 1;for(int i = 1;i < n;++i){if(dominoes[i] == '.'){if(dp[i-1] > 0)dp[i] = dp[i-1]+1;}else if(dominoes[i] == 'R')dp[i] = 1;elsedp[i] = -1;}for(int i = n-1;i >= 0;--i){if(dominoes[i] == '.'){if(i < n-1 && dp[i+1] < 0){if(dp[i] + dp[i+1]-1 > 0)dp[i] = dp[i+1]-1;else if(dp[i]+dp[i+1]-1 == 0)dp[i] = 0;else if(dp[i] <= 0)dp[i] = dp[i+1]-1;}if(dp[i] == 0)dominoes[i] = '.';else if(dp[i] > 0)dominoes[i] = 'R';else dominoes[i] = 'L';}}return dominoes;}
};

ak截图：

OJ题13：将字符串翻转到单调递增 难度分:1602

这里是题目

题目解析

算法原理

我们使用动态规划来解决一下这道题。

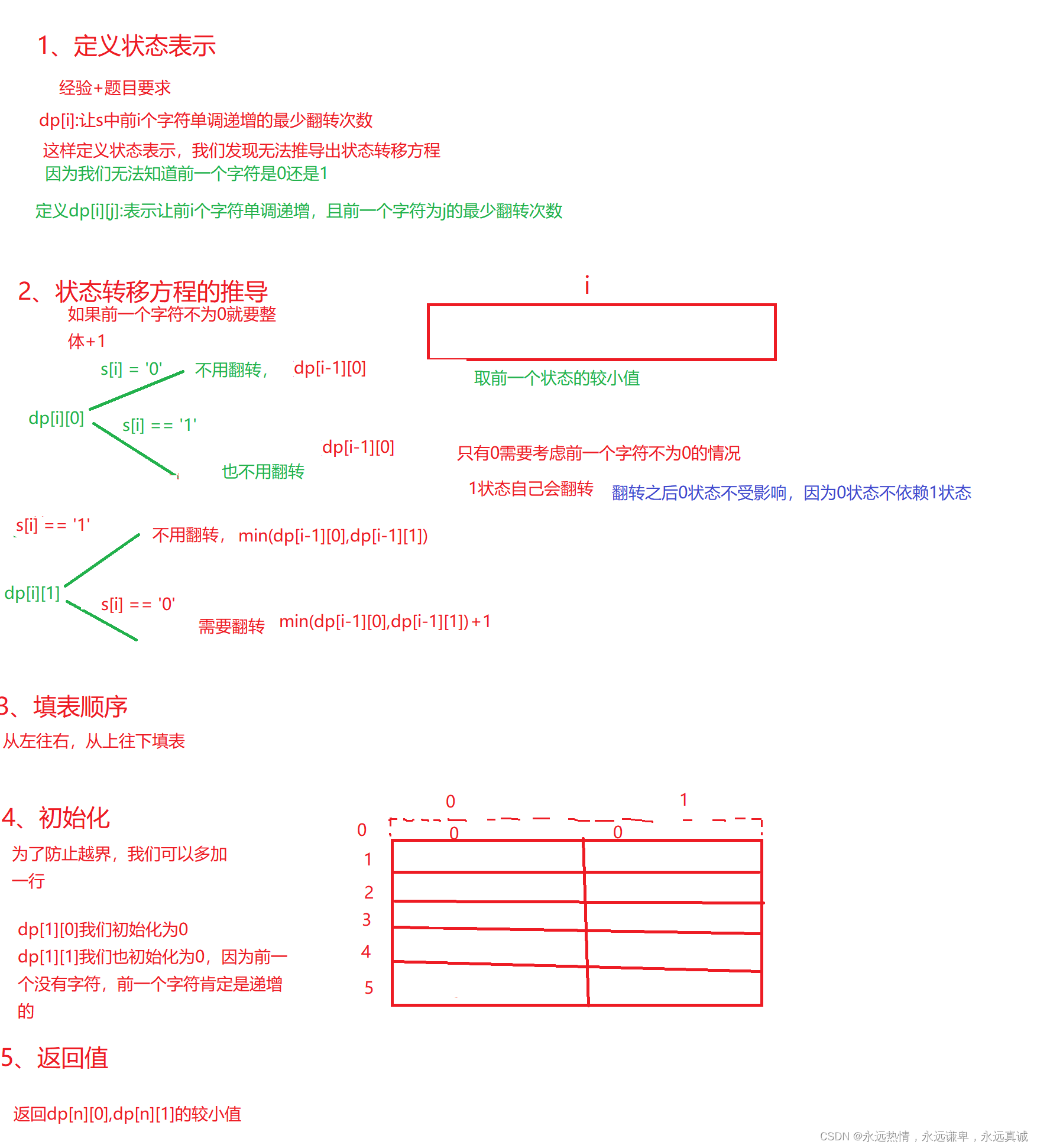
代码实现

class Solution {
public:int minFlipsMonoIncr(string s) {//创建dp表//初始化//填表//返回值int n = s.size();vector<vector<int>> dp(n+1,vector<int>(2));for(int i = 2;i <= n;++i){if(s[i-1] == '0'){dp[i][0] = dp[i-1][0];if(s[i-2] != '0')dp[i][0]++;dp[i][1] = min(dp[i-1][0],dp[i-1][1])+1;}else//s[i-1] == '1'{dp[i][0] = dp[i-1][0];if(s[i-2] != '0')dp[i][0]++;dp[i][1] = min(dp[i-1][0],dp[i-1][1]);} }return min(dp[n][1],dp[n][0]);}
};

ak截图：

滚动数组优化

0和1状态只依赖之前的一个状态，我们可以使用滚动数组优化。

代码实现：

class Solution {
public:int minFlipsMonoIncr(string s) {//创建dp表//初始化//填表//返回值int n = s.size();vector<int> dp(2);for(int i = 2;i <= n;++i){if(s[i-1] == '0'){dp[1] = min(dp[0],dp[1])+1;if(s[i-2] != '0')dp[0]++;}else//s[i-1] == '1'{dp[1] = min(dp[0],dp[1]);if(s[i-2] != '0')dp[0]++; 
}}return min(dp[1],dp[0]);}
};

这里注意初始化顺序，保证我们用到之前那个状态时它还没被覆盖即可。

ak截图：

OJ题14：骑士拨号器 难度分:1690

这里是题目

题目解析

算法原理

下面我们使用动态规划来解决一下这道题。

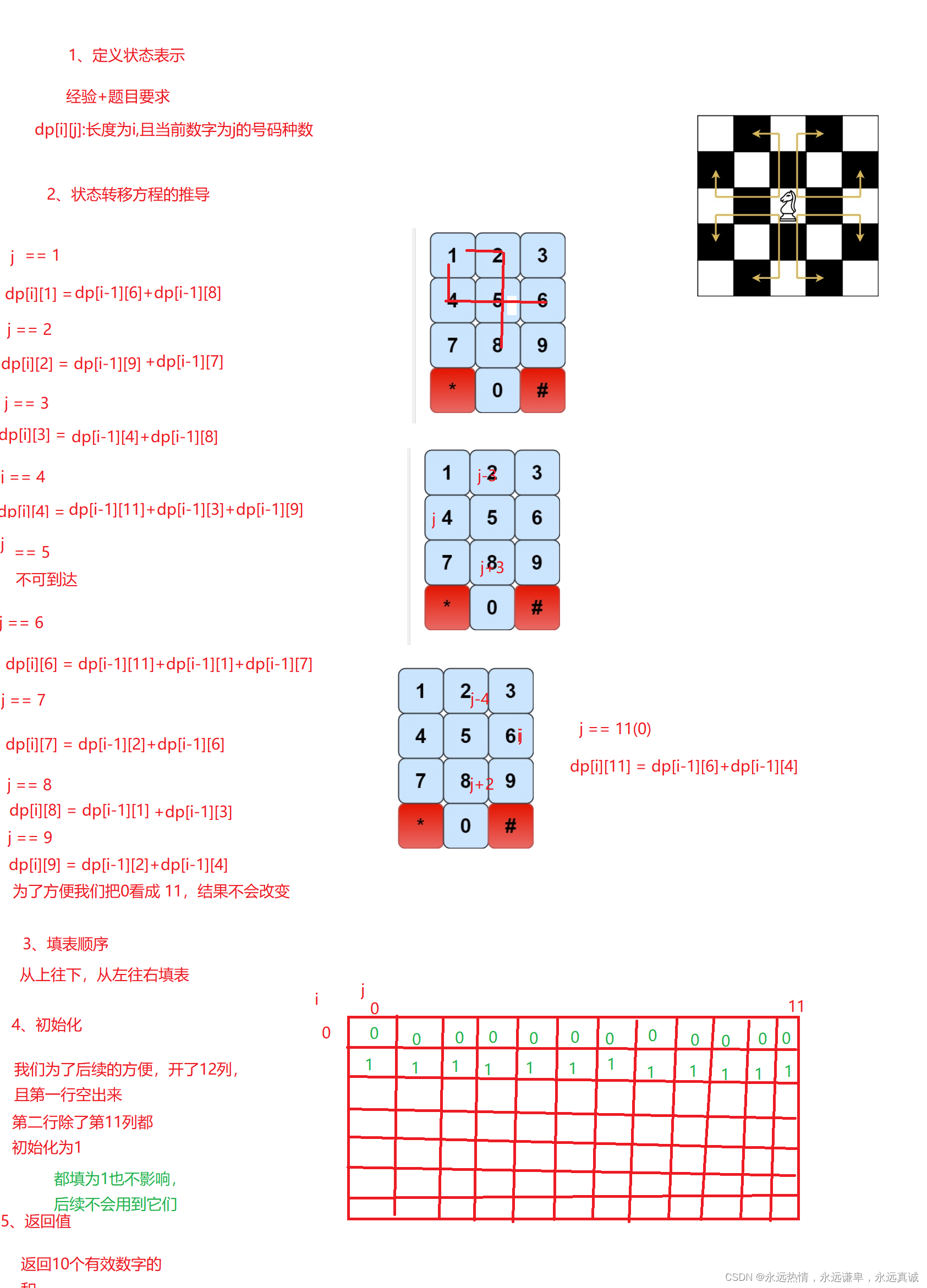
代码实现

class Solution {
public:int knightDialer(int n) {//创建dp表//初始化//填表//返回值const int MOD = 1e9+7;vector<vector<long long>> dp(n+1,vector<long long>(12,0));for(int j = 0;j < 12;++j)dp[1][j] = 1;for(int i = 2;i <= n;++i)for(int j = 1;j < 12;++j){switch(j){case 1:dp[i][j] = (dp[i-1][6]+dp[i-1][8])%MOD;break;case 2:dp[i][j] =  (dp[i-1][9]+dp[i-1][7])%MOD;break;case 3:dp[i][j] =  (dp[i-1][4]+dp[i-1][8])%MOD;break;case 4:dp[i][j] =  (dp[i-1][11]+dp[i-1][3]+dp[i-1][9])%MOD;break;case 6:dp[i][j] =  (dp[i-1][11]+dp[i-1][1]+dp[i-1][7])%MOD;break;case 7:dp[i][j] =  (dp[i-1][2]+dp[i-1][6])%MOD;break;case 8:dp[i][j] =  (dp[i-1][1]+dp[i-1][3])%MOD;break;case 9:dp[i][j] =  (dp[i-1][2]+dp[i-1][4])%MOD;break;case 11:dp[i][j] =  (dp[i-1][6]+dp[i-1][4])%MOD;break;default:break;}}long long ret = 0;for(int j = 1;j < 12;++j){if(j != 10)ret += dp[n][j];}return ret%MOD;}
};

ak截图：

滚动数组优化

这里虽然我们当前行的状态可能会互相用不同列的状态，我们开一个新的数组把原来的数组的值保存一下还是可以使用达到空间优化的效果。

代码实现：

class Solution {
public:int knightDialer(int n) {//创建dp表//初始化//填表//返回值if(n == 1)return 10;const int MOD = 1e9+7;vector<int> dp(12,0);for(int j = 0;j < 12;++j)dp[j] = 1;for(int i = 2;i <= n;++i){vector<int> dp1(dp);for(int j = 1;j < 12;++j){switch(j){case 1:dp[j] = (dp1[6]+dp1[8])%MOD;break;case 2:dp[j] =  (dp1[9]+dp1[7])%MOD;break;case 3:dp[j] =  (dp1[4]+dp1[8])%MOD;break;case 4:dp[j] =  (0LL+dp1[11]+dp1[3]+dp1[9])%MOD;break;case 6:dp[j] =  (0LL+dp1[11]+dp1[1]+dp1[7])%MOD;break;case 7:dp[j] =  (dp1[2]+dp1[6])%MOD;break;case 8:dp[j] =  (dp1[1]+dp1[3])%MOD;break;case 9:dp[j] =  (dp1[2]+dp1[4])%MOD;break;case 11:dp[j] =  (dp1[6]+dp1[4])%MOD;break;default:break;}}}long long ret = 0;for(int j = 1;j < 12;++j){if(j != 10 && j != 5)ret += dp[j];}return ret%MOD;}
};

• 注意：我们的中间结果可能溢出，我们在加法的前面加上0LL(long long类型的0），就可以把int类型加法转化为long long类型的加法，然后模上一个值，int就不会溢出了。

ak截图：

也可以使用状态机来求解，优化的关键是要找出数字之间的对称关系已达到状态压缩的目的，把图画好，可以参考这篇题解

OJ题15：掷骰子等于目标和的方法数 难度分:1654—分组背包

这里是题目

题目解析

算法原理

下面我们使用动态规划来解决一下这道题。

代码实现

class Solution {
public:int numRollsToTarget(int n, int k, int target) {//创建dp表//初始化//填表//返回值const int MOD = 1e9+7;vector<vector<int>> dp(n+1,vector<int>(target+1));dp[0][0] = 1;for(int i = 1;i <= n;++i)for(int j = 1;j <= target;++j)for(int x = 1;x <= k;++x){if(j-x >= 0)dp[i][j] = (0LL+dp[i][j]+dp[i-1][j-x])%MOD;}return dp[n][target];}
};

ak截图：

滚动数组优化

我们观察到，dp[i][j]所依赖的状态都是j比它小的值，所以我们第二维倒着遍历，保证我们用到这个状态的时候，它还没有被更新为最新一行的值，注意每一个j状态更新前都要将其赋值为0，因为上一行的值对我们这行已经不起作用了。

代码实现：

class Solution {
public:int numRollsToTarget(int n, int k, int target) {//创建dp表//初始化//填表//返回值const int MOD = 1e9+7;vector<int> dp(target+1);dp[0] = 1;for(int i = 1;i <= n;++i)for(int j = target;j >= 0;--j){dp[j] = 0;for(int x = 1;x <= k;++x){if(j-x >= 0){dp[j] = (0LL+dp[j]+dp[j-x])%MOD;}}}return dp[target];}
};

ak截图：