还会持续更新

动态规划

什么是动态规划？

斐波那契模型

三步问题

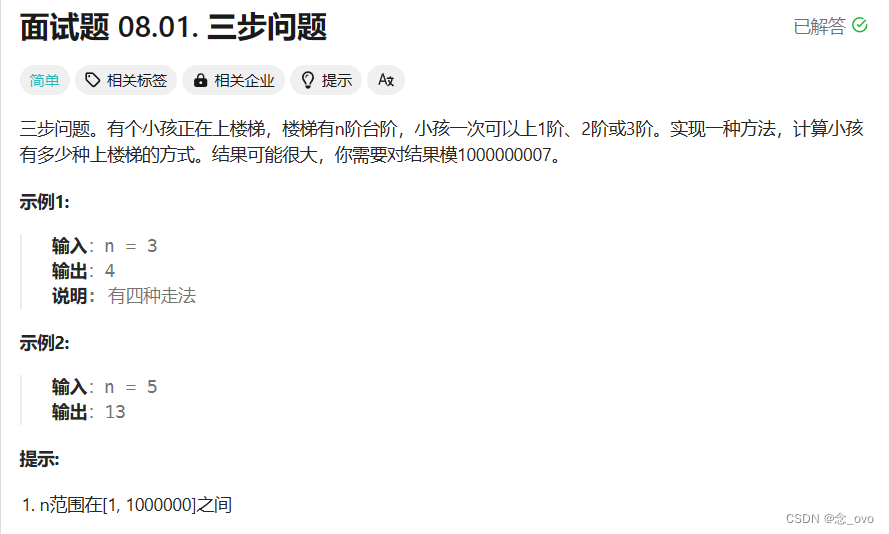
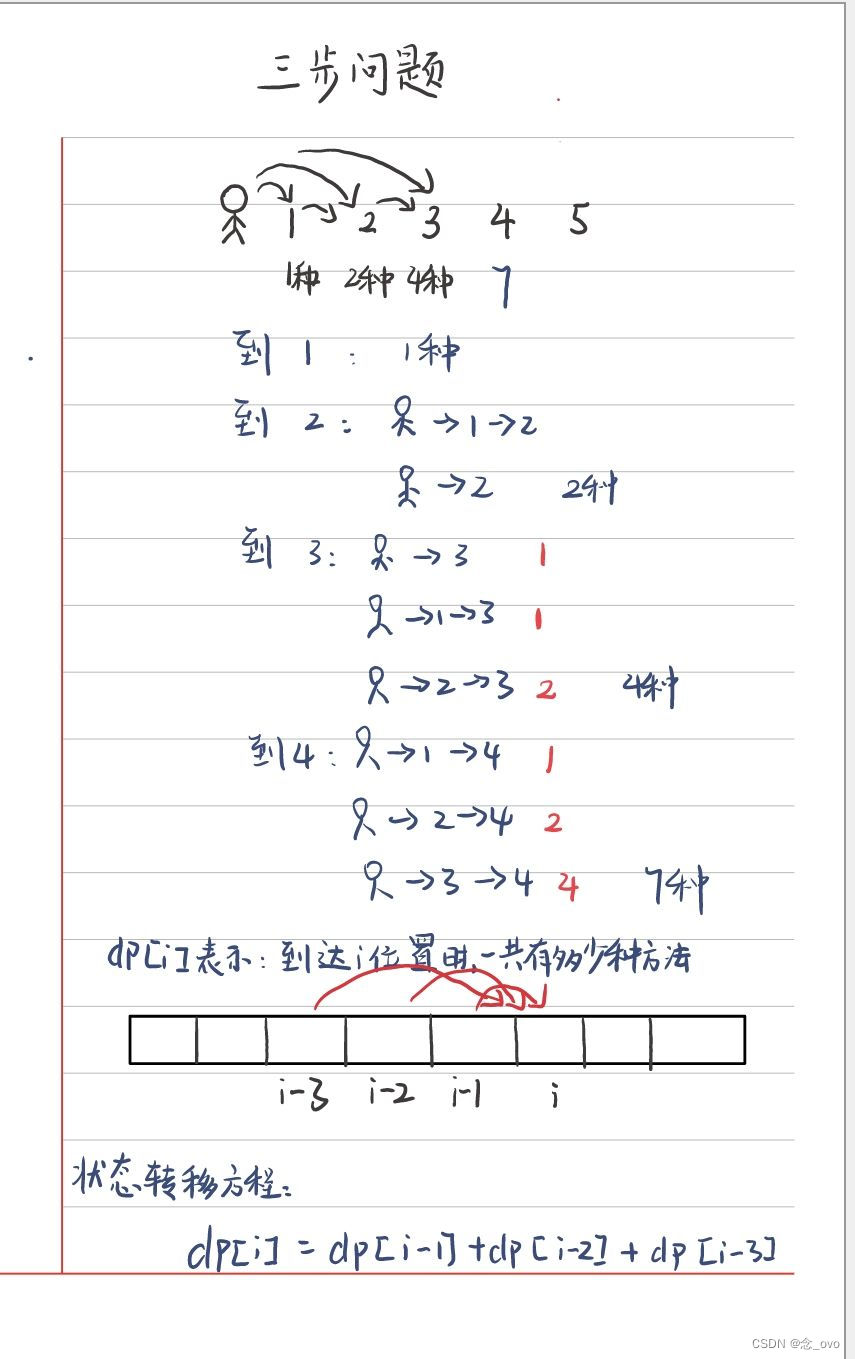
class Solution {
public: const int N = 1000009;int waysToStep(int n) {if(n==1) return 1;if(n==2) return 2;if(n==3) return 4;int dp[N];dp[1] = 1;dp[2] = 2; dp[3] = 4;for(int i =4;i<=n;i++){dp[i]=((dp[i-1] + dp[i-2])%1000000007 + dp[i-3])%1000000007;//结果太大，遇到相加相乘都要取模}        return dp[n];}
};

最小花费爬楼梯

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {//创建dp表vector<int> dp(cost.size()+1);//边界情况讨论//初始化dp[0] = dp[1] = 0;for(int i =2;i<=cost.size();i++){dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[cost.size()];}
};

路径问题

不同路径

class Solution {
public:int uniquePaths(int m, int n) {//创建dp表vector<vector<int>> dp(m+1,vector<int>(n+1));//边界和初始化for(int i = 0;i<=m;i++){dp[i][0] = 0;}for(int j =0;j<=n;j++){dp[0][j] = 0;}dp[0][1] = 1;//填表for(int i =1;i<=m;i++){for(int j =1;j<=n;j++){dp[i][j] = dp[i-1][j]+dp[i][j-1];}}//使用表return dp[m][n];}
};

路径问题Ⅱ

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& arr) {//创建dp表int n = arr.size();int m = arr[0].size();vector<vector<int>> dp(n+1,vector<int>(m+1));//初始化dp[0][1] = 1;//填表for(int i = 1;i<=n;i++){for(int j = 1;j<=m;j++){if(arr[i-1][j-1] == 0)dp[i][j] = dp[i-1][j]+dp[i][j-1];}}return dp[n][m];}
};

简单多状态

按摩师

class Solution {
public:int massage(vector<int>& nums) {//创建dp表int n = nums.size();if(n==0) return 0;vector<int> f(n+1);vector<int> g(n+1);//初始化//边界问题f[1] = nums[0];g[1] = 0;//填表for(int i =2; i<=n;i++){f[i] = g[i-1] + nums[i-1];g[i] = max(f[i-1],g[i-1]);}//用表return max(f[n],g[n]);}
};