• 梯度下降算法(Gradient Descent)
• 梯度下降算法几种变体

梯度下降算法(Gradient Descent)

梯度下降算法是一种用于求解函数最小值的一阶优化算法。在机器学习和深度学习中，梯度下降算法被广泛用于模型训练，通过迭代的方式调整模型参数，以最小化损失函数。

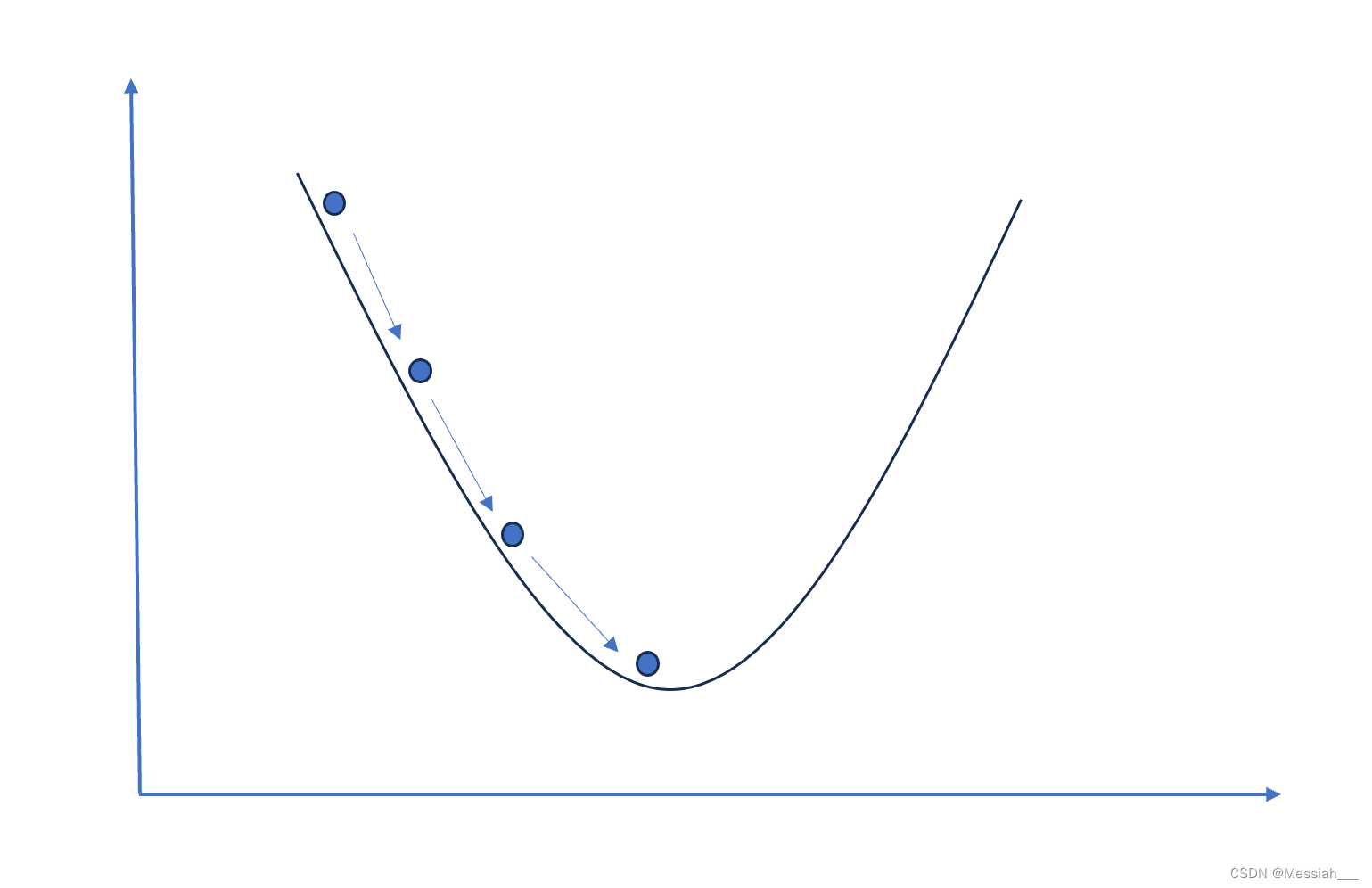
梯度下降算法的基本思想是：在函数的梯度（或者说斜率）指向的方向上，函数值下降得最快。因此，如果我们想要找到函数的最小值，可以从函数的某个初始点出发，沿着梯度的反方向（因为我们要减小函数值）逐步迭代，最终达到函数的局部最小值点。

梯度下降算法的迭代公式通常表示为：$x_{new}=x_{old}-\alpha \nabla f(x_{old})$

其中：

• $x_{old}$是当前迭代点的坐标。
• $\alpha$ 是学习率（步长），它决定了在梯度方向上每一步前进的距离。
• $\nabla f(x_{old})$ 是函数 $f(x)$ 在点 $x_{old}$的梯度，它是一个向量，指向函数增长最快的方向。
• $x_{new}$ 是下一个迭代点的坐标。

梯度下降算法几种变体

假设有一个损失函数 $J(\theta )$，其中 $\theta$ 是模型参数，我们的目标是通过调整 $\theta$ 来最小化损失函数。

1. 批量梯度下降（Batch Gradient Descent）：

批量梯度下降使用所有训练样本来计算梯度，然后更新参数。其更新规则可以表示为：

$$\theta =\theta -\alpha \cdot \nabla J(\theta )$$

其中，$\alpha$ 是学习率，$\nabla J(\theta )$ 是损失函数 $J(\theta )$ 关于参数 $\theta$ 的梯度。批量梯度下降的更新规则考虑了所有样本的梯度信息，因此可以保证每次更新的方向是最优的，但计算量较大。

2. 随机梯度下降（Stochastic Gradient Descent）：

随机梯度下降每次只使用一个随机样本来计算梯度，并根据该梯度更新参数。其更新规则可以表示为：

$$\theta =\theta -\alpha \cdot \nabla J(\theta ;x^{(i)},y^{(i)})$$

其中，$(x^{(i)},y^{(i)})$ 是随机选择的一个训练样本，$\nabla J(\theta ;x^{(i)},y^{(i)})$ 是损失函数 $J(\theta )$ 关于参数 $\theta$ 在样本 $(x^{(i)},y^{(i)})$ 处的梯度。随机梯度下降每次更新只考虑一个样本，因此更新的方向可能不是最优的，但计算量较小。

3. 小批量梯度下降（Mini-batch Gradient Descent）：

小批量梯度下降是批量梯度下降和随机梯度下降的折中，每次更新使用一小部分（批量）样本来计算梯度，并根据平均梯度更新参数。其更新规则可以表示为：
$$\theta =\theta -\alpha \cdot \frac{1}{|\mathcal{B}|}\sum _{(x^{(i)},y^{(i)})\in \mathcal{B}}\nabla J(\theta ;x^{(i)},y^{(i)})$$
其中，$\mathcal{B}$ 是随机选择的小批量样本集合，$|\mathcal{B}|$ 是批量大小，$\nabla J(\theta ;x^{(i)},y^{(i)})$ 是损失函数 $J(\theta )$ 关于参数 $\theta$ 在批量样本 $(x^{(i)},y^{(i)})$ 处的梯度。小批量梯度下降综合了批量梯度下降和随机梯度下降的优点，既可以保证一定的更新稳定性，又可以减少计算量。