理论基础

二叉树的分类：

二叉树的种类：

满二叉树

满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

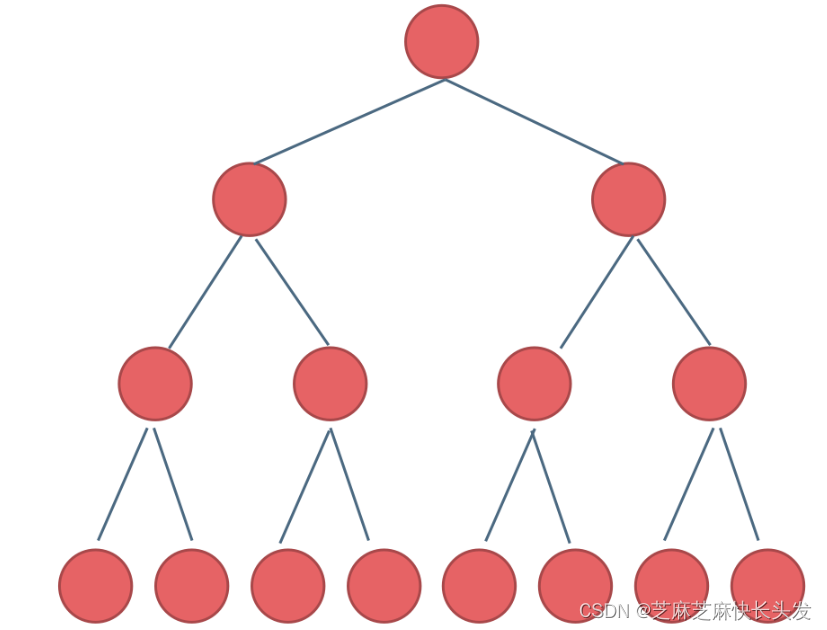
这棵二叉树为满二叉树，也可以说深度为k，有2^k-1个节点的二叉树。（k从1开始）

完全二叉树

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1) 个节点。

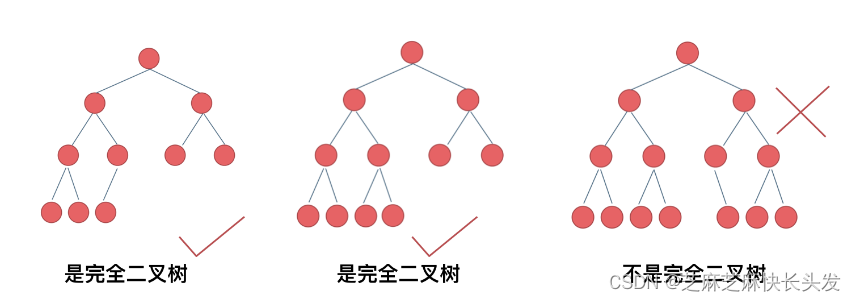
之前我们刚刚讲过优先级队列其实是一个堆，堆就是一棵完全二叉树，同时保证父子节点的顺序关系。

二叉搜索树

前面介绍的树，都没有数值的，而二叉搜索树是有数值的了，二叉搜索树是一个有序树。

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树

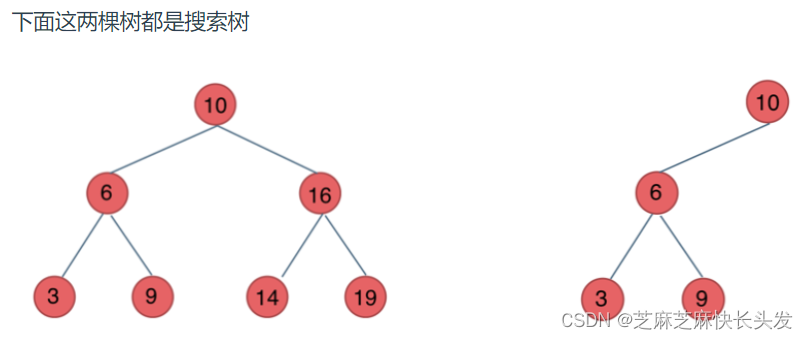
平衡二叉搜索树

平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

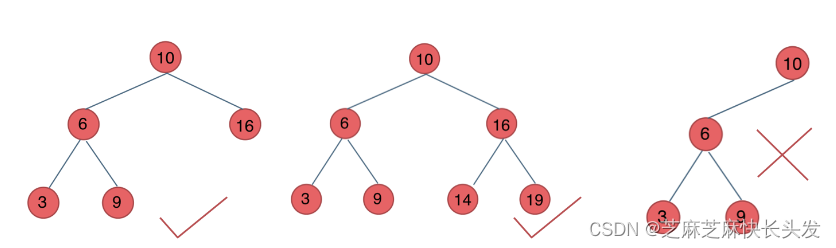
最后一棵 不是平衡二叉树，因为它的左右两个子树的高度差的绝对值超过了1。

C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是logn，注意我这里没有说unordered_map、unordered_set，unordered_map、unordered_set底层实现是哈希表。

二叉树的存储方式：

二叉树可以链式存储，也可以顺序存储。
那么链式存储方式就用指针， 顺序存储的方式就是用数组。
顾名思义就是顺序存储的元素在内存是连续分布的，而链式存储则是通过指针把分布在各个地址的节点串联一起。

链式存储

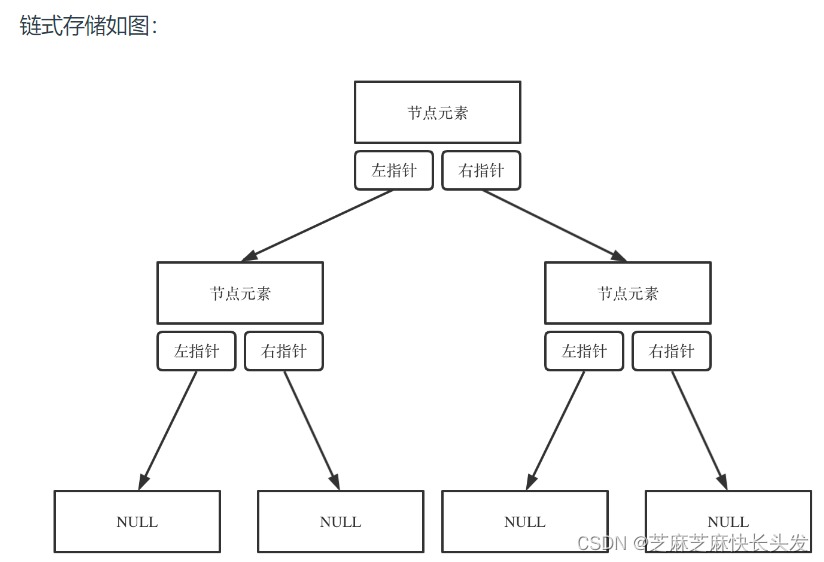
顺序存储

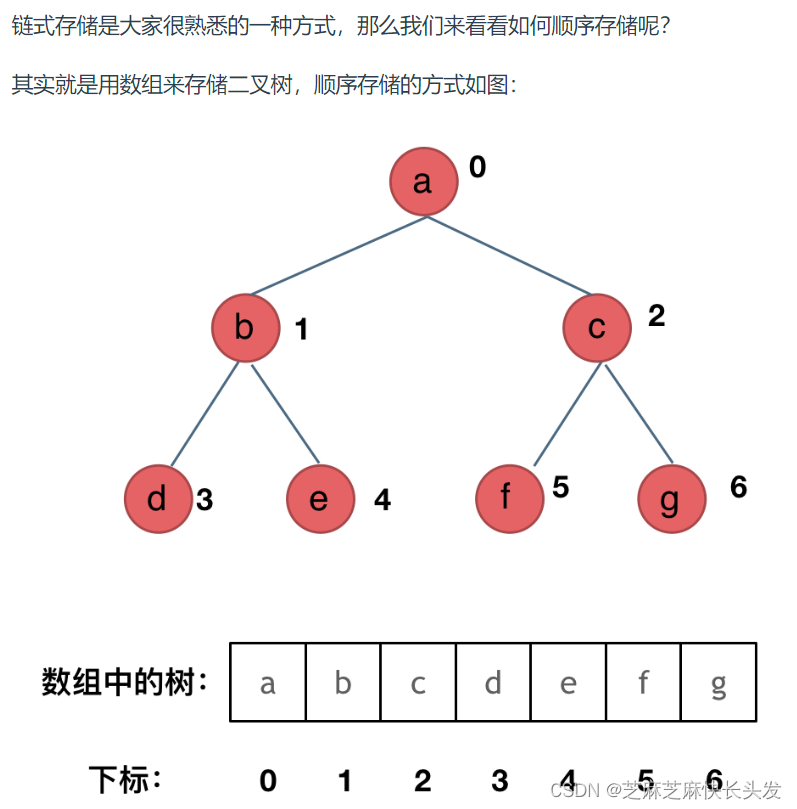
如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。
但是用链式表示的二叉树，更有利于我们理解，所以一般我们都是用链式存储二叉树。

所以大家要了解，用数组依然可以表示二叉树。

二叉树的遍历方式：

二叉树主要有两种遍历方式：

1. 深度优先遍历：先往深走，遇到叶子节点再往回走。
2. 广度优先遍历：一层一层的去遍历。

这两种遍历是图论中最基本的两种遍历方式。
深度优先遍历
3. 前序遍历（递归法，迭代法）
4. 中序遍历（递归法，迭代法）
5. 后序遍历（递归法，迭代法）
广度优先遍历
6. 层次遍历（迭代法）

这里前中后序，其实指的就是中间节点的遍历顺序，只要大家记住 前中后序指的就是中间节点的位置就可以了。
看如下中间节点的顺序，就可以发现，中间节点的顺序就是所谓的遍历方式：

• 前序遍历：中左右
• 中序遍历：左中右
• 后序遍历：左右中
  

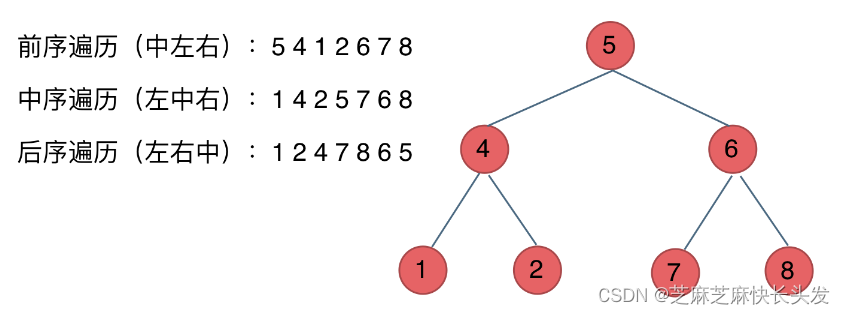
深度优先和广度优先遍历实现方式

我们做二叉树相关题目，经常会使用递归的方式来实现深度优先遍历，也就是实现前中后序遍历，使用递归是比较方便的。
之前我们讲栈与队列的时候，就说过栈其实就是递归的一种实现结构，也就说前中后序遍历的逻辑其实都是可以借助栈使用递归的方式来实现的。
而广度优先遍历的实现一般使用队列来实现，这也是队列先进先出的特点所决定的，因为需要先进先出的结构，才能一层一层的来遍历二叉树。

二叉树的定义：

我们来看看链式存储的二叉树节点的定义方式：

struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

大家会发现二叉树的定义 和链表是差不多的，相对于链表 ，二叉树的节点里多了一个指针， 有两个指针，指向左右孩子。
TreeNode(int x) : val(x), left(NULL), right(NULL) {}的意思是创建一个新的TreeNode对象，其值为x，并且它的左右子节点都被初始化为NULL。

---

递归遍历

递归三要素：

介绍前后中序的递归写法，要通过简单题目把方法论确定下来，有了方法论，后面才能应付复杂的递归。
这里确定下来递归算法的三个要素。每次写递归，都按照这三要素来写：

1. 确定递归函数的参数和返回值： 确定哪些参数是递归的过程中需要处理的，那么就在递归函数里加上这个参数， 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
2. 确定终止条件： 写完了递归算法, 运行的时候，经常会遇到栈溢出的错误，就是没写终止条件或者终止条件写的不对，操作系统也是用一个栈的结构来保存每一层递归的信息，如果递归没有终止，操作系统的内存栈必然就会溢出。
3. 确定单层递归的逻辑： 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。

举例子：

以前序遍历为例：（中左右）
4. 确定递归函数的参数和返回值： 因为要打印出前序遍历节点的数值，所以参数里需要传入vector数组来放节点的数值，还要再放一个根节点，除此之外就不需要再处理什么数据了也不需要有返回值，所以递归函数返回类型就是void，代码如下：

void traversal(TreeNode* cur, vector<int>& vec)

5. 确定终止条件： 在递归的过程中，如何算是递归结束了呢，当然是当前遍历的节点是空了，那么本层递归就要结束了，所以如果当前遍历的这个节点是空，就直接return，返回到上一层的递归中，代码如下：

if (cur == NULL) return;

确定单层递归的逻辑： 前序遍历是中左右的循序，所以在单层递归的逻辑，是要先取中节点的数值，再取左节点的数值，最后取右节点的数值。代码如下：

vec.push_back(cur->val);    // 中
traversal(cur->left, vec);  // 左
traversal(cur->right, vec); // 右

单层递归的逻辑就是按照中左右的顺序来处理的，这样二叉树的前序遍历，基本就写完了。

前序遍历：

class Solution {
public:void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;vec.push_back(cur->val);    // 中traversal(cur->left, vec);  // 左traversal(cur->right, vec); // 右}vector<int> preorderTraversal(TreeNode* root) {vector<int> result;traversal(root, result);return result;}
};

中序遍历：

void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal(cur->left, vec);  // 左vec.push_back(cur->val);    // 中traversal(cur->right, vec); // 右
}

后序遍历：

void traversal(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal(cur->left, vec);  // 左traversal(cur->right, vec); // 右vec.push_back(cur->val);    // 中
}