-
题目描述(力扣题库115):
-
给你两个字符串
s和t,统计并返回在s的 子序列 中t出现的个数,结果需要对 109 + 7 取模。示例 1:
输入:s = "rabbbit", t = "rabbit"
输出:3解释: 如下所示, 有 3 种可以从 s 中得到"rabbit" 的方案。rabbbitrabbbitrabbbit 
-
-
解题思想:
-
动态规划 :
-
当解决动态规划问题时,通常需要定义一个状态数组来存储中间结果。在这个问题中,我们使用二维数组 `dp` 来表示状态。`dp[i][j]` 表示在字符串 `s` 的子串 `s[i:]` 中出现字符串 `t` 的子串 `t[j:]` 的次数。
首先,我们从字符串的末尾开始向前遍历。这是因为我们需要依赖后面的状态来计算当前状态。我们将 `dp[i][t.length()]` 初始化为 1,因为对于任何非空字符串 `s`,其末尾与空字符串匹配的次数都是 1。
然后,我们从 `s` 和 `t` 的末尾开始逐个字符进行比较。如果 `s[i]` 与 `t[j]` 相等,则意味着我们有两种选择:
1. 保留 `s[i]`,并且尝试匹配 `s[i + 1:]` 和 `t[j + 1:]`,所以此时的状态转移方程为 `dp[i][j] = dp[i + 1][j + 1]`。
2. 匹配 `s[i]` 和 `t[j]`,然后尝试匹配 `s[i + 1:]` 和 `t[j:]`,所以此时的状态转移方程为 `dp[i][j] += dp[i + 1][j]`。如果 `s[i]` 与 `t[j]` 不相等,则意味着我们不能匹配当前字符,只能选择保留 `s[i]` 并尝试匹配 `s[i + 1:]` 和 `t[j:]`,所以状态转移方程为 `dp[i][j] = dp[i + 1][j]`。
通过不断地更新状态数组 `dp`,最终我们就可以得到整个字符串 `s` 和 `t` 的子序列匹配次数,即 `dp[0][0]`。
这种动态规划的解法利用了子问题的重叠性质,避免了重复计算,从而实现了高效的解决方案。
-
-
解题步骤:
-
初始化状态数组:
- 创建一个二维数组
dp,其大小为(s.length() + 1) × (t.length() + 1)。 - 初始化
dp[i][t.length()] = 1,表示任何非空字符串s的末尾与空字符串匹配的次数都是 1。
- 创建一个二维数组
-
逆向遍历字符串:
- 从
s和t的末尾开始向前遍历字符。 - 遍历的范围是
i = s.length() - 1到0,以及j = t.length() - 1到0。
- 从
-
状态转移:
- 对于当前位置
(i, j),判断s[i]和t[j]是否相等:- 如果相等,则有两种选择:
- 保留
s[i],并尝试匹配s[i + 1:]和t[j + 1:],更新状态:dp[i][j] = dp[i + 1][j + 1]。 - 匹配
s[i]和t[j],并尝试匹配s[i + 1:]和t[j:],更新状态:dp[i][j] += dp[i + 1][j]。
- 保留
- 如果不相等,则只能保留
s[i],并尝试匹配s[i + 1:]和t[j:],更新状态:dp[i][j] = dp[i + 1][j]。
- 如果相等,则有两种选择:
- 对于当前位置
-
返回结果:
最终的结果存储在dp[0][0]中,表示整个字符串s和t的子序列匹配次数。
通过以上步骤,可以得到字符串 s 和 t 的子序列匹配次数。这个算法的时间复杂度为 O(mn),其中 m 是字符串 s 的长度,n 是字符串 t 的长度。
- 以下是代码实现:
-
class Solution {public int numDistinct(String s, String t){if(s.length() < t.length()) return 0;int[][] dp = new int[s.length() + 1][t.length() + 1];for (int i = 0; i <= s.length(); i++) {dp[i][t.length()] = 1;}for (int i = s.length() - 1; i >= 0; i--) {for (int j = t.length() - 1; j >= 0; j--) {if(s.charAt(i) == t.charAt(j))dp[i][j] = dp[i + 1][j + 1] + dp[i + 1][j];elsedp[i][j] = dp[i + 1][j];}}return dp[0][0];} }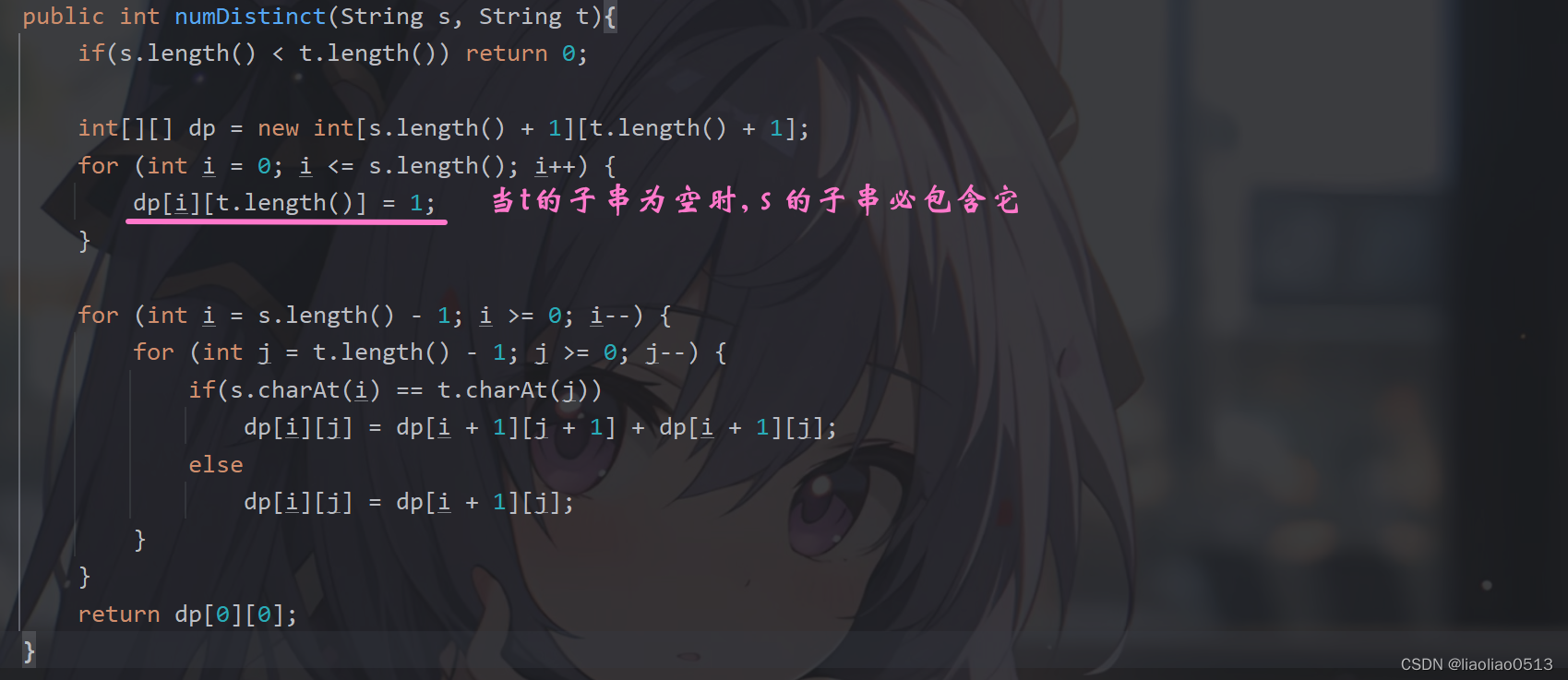
-
- 以上是本篇文章的全部内容, 感谢观看








)


)





)
)
