【Leetcode每日一题】递归 - 二叉树剪枝（难度⭐⭐）（50）

1. 题目解析

题目链接：814. 二叉树剪枝

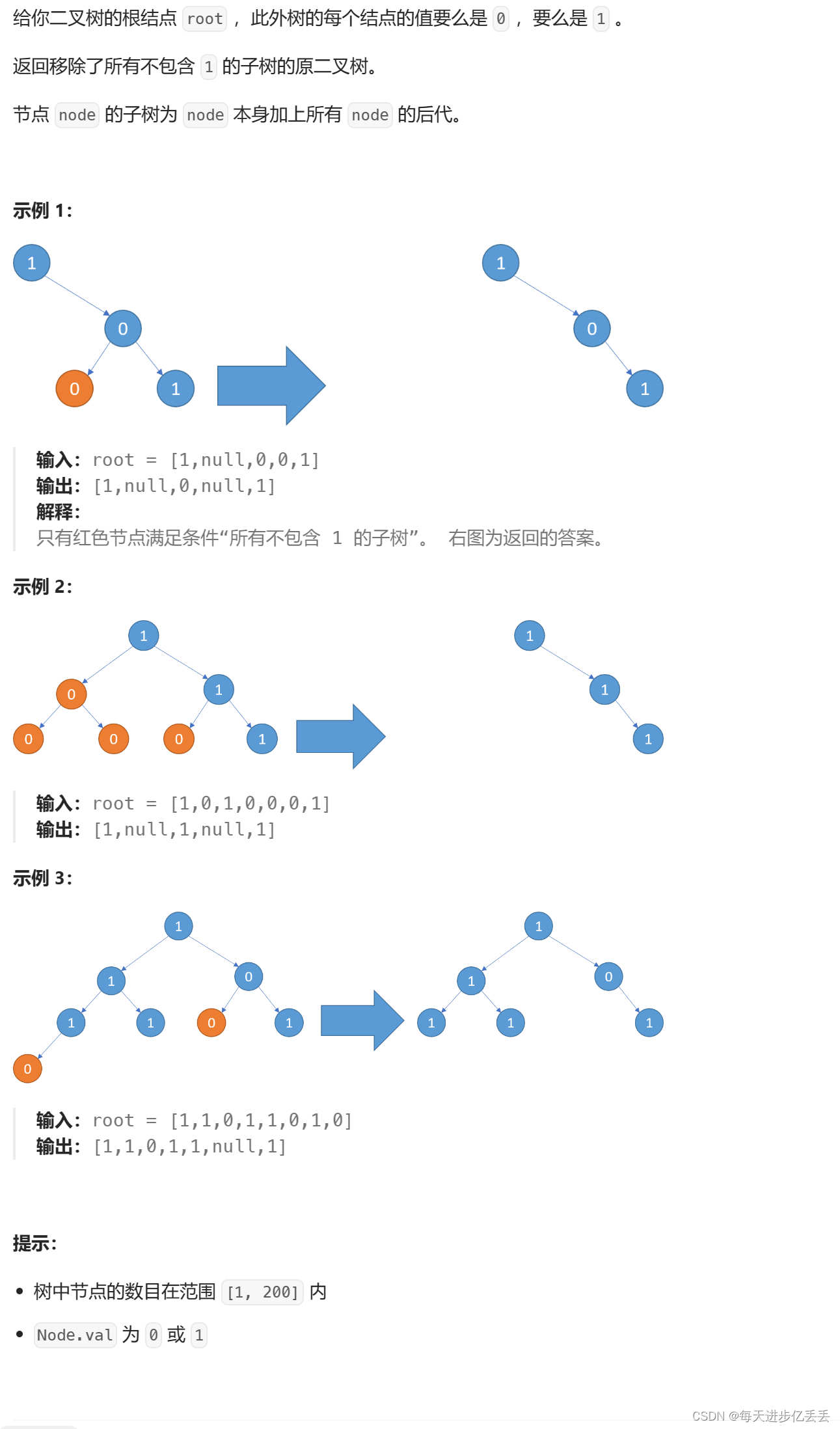
这个问题的理解其实相当简单，只需看一下示例，基本就能明白其含义了。

2.算法原理

想象一下，你有一堆层层叠叠的积木，你想从底部开始，把那些标记为0的积木拿走。如果直接从上面开始拿，你可能会碰到很多麻烦，因为你不知道下面的积木长什么样，也不敢轻易动它们。但是，如果你从最下面的积木开始，一层一层往上拿，事情就变得简单多了。

这就像我们处理二叉树一样。如果从上往下删除节点，我们就需要知道左右子树的情况，这确实是个头疼的问题。但反过来，如果我们从下往上，也就是从最底层的叶子节点开始，删除那些值为0的叶子节点，然后再处理上一层，这样问题就简单多了。

具体来说，我们可以采用后序遍历的方法。后序遍历就是先处理左子树，再处理右子树，最后处理当前节点。当我们处理到当前节点时，只要判断它是不是叶子节点，并且值是不是0，如果是的话，就直接删除它。

不过要注意，当我们删除一个叶子节点后，它的父节点可能就变成新的叶子节点了。所以，处理完当前节点后，我们还需要检查它的父节点是否需要处理。这就是为什么我们选择后序遍历的原因，因为后序遍历最先遍历到的总是叶子节点。

算法流程可以这样描述：

定义一个递归函数：dfs(TreeNode*& root)，这个函数会检查当前节点是否需要删除。
递归的出口：如果传入的节点为空，那么直接返回，不需要做任何处理。
递归处理左右子树：先调用dfs函数处理左子树，再处理右子树。
处理当前节点：
- 判断当前节点是否已经是叶子节点（即左右子节点都被删除了），并且节点的值为0。
- 如果是的话，就删除这个节点。
- 如果不是，就保持原样，不做任何处理。

通过这样的方式，我们可以从底部开始，逐步删除值为0的叶子节点，并且保证删除后的树仍然满足我们的要求。当所有的叶子节点都被检查并处理完毕后，如果它们的值都是1，那就说明整棵树都包含1，此时我们就可以返回结果了。

这种方法的好处是，它让删除操作变得相对简单，而且不会影响最终的结果。就像我们一层一层地拿走积木，最后留下的都是我们想要的。

3.代码编写

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution 
{
public:TreeNode* pruneTree(TreeNode* root) {if(root == nullptr) return nullptr;root->left = pruneTree(root->left);root->right = pruneTree(root->right);if(root->left == nullptr && root->right == nullptr && root->val == 0){delete root;root = nullptr;}return root;}
};