(7)积木画
题目:
小明最近迷上了积木画, 有这么两种类型的积木, 分别为 �I 型(大小为 2 个单位面积) 和 �L 型 (大小为 3 个单位面积):
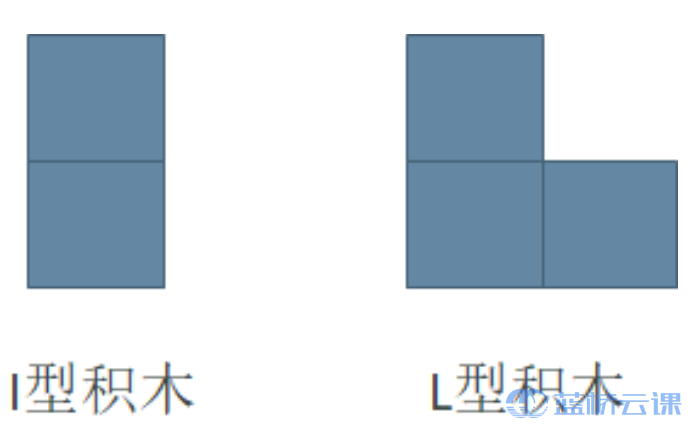
同时, 小明有一块面积大小为 2×�2×N 的画布, 画布由 2×�2×N 个 1×11×1 区域构 成。小明需要用以上两种积木将画布拼满, 他想知道总共有多少种不同的方式? 积木可以任意旋转, 且画布的方向固定。
输入格式
输入一个整数 �N,表示画布大小。
输出格式
输出一个整数表示答案。由于答案可能很大,所以输出其对 1000000007 取模后的值。
样例输入
3
样例输出
5
样例说明
五种情况如下图所示,颜色只是为了标识不同的积木:
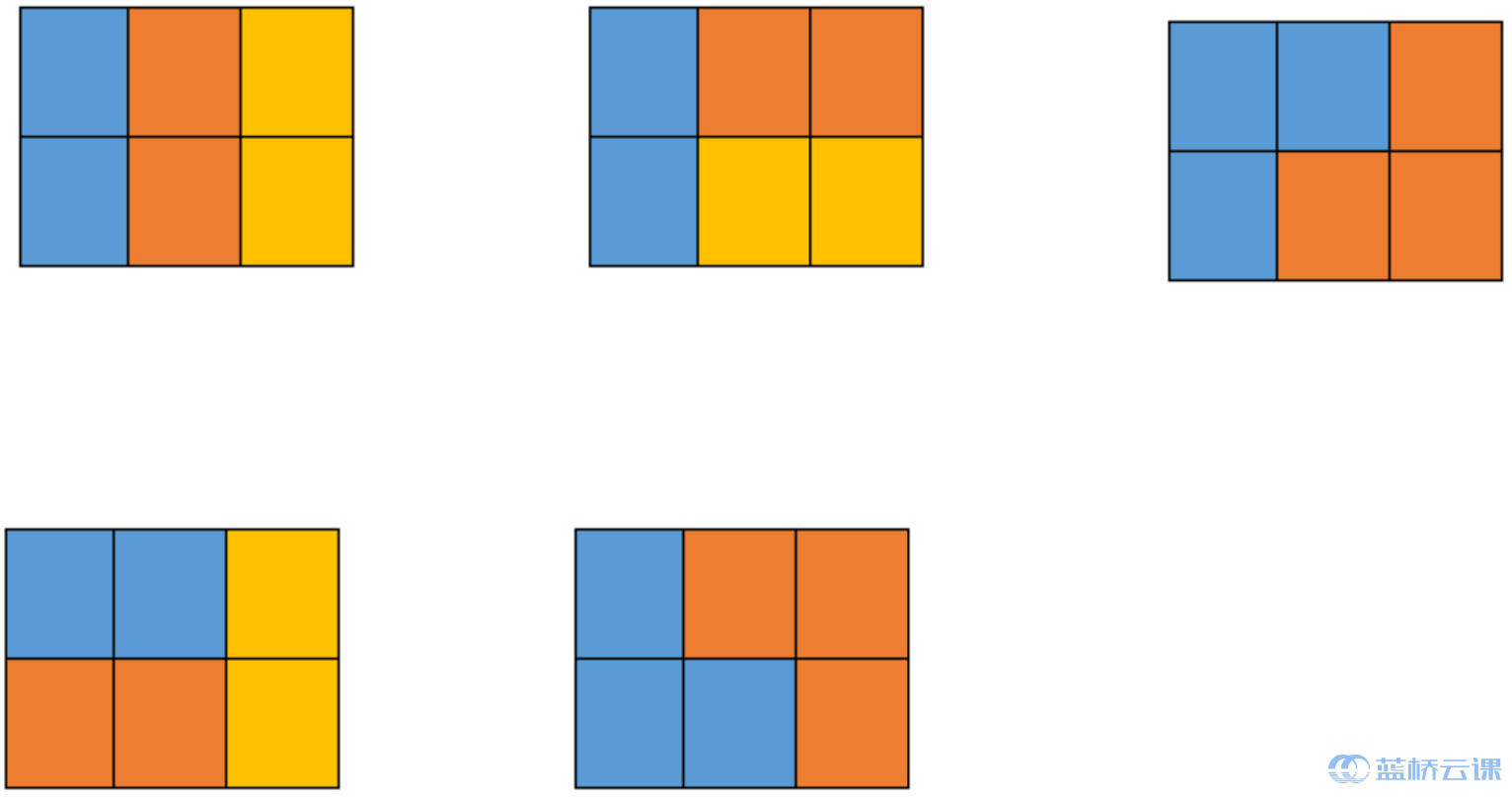
评测用例规模与约定
对于所有测试用例,1≤�≤100000001≤N≤10000000.
笔记:
这道题是一道dp的题目,首先我们要找到状态转移的思路:这里我们可以从下标为0开始向前找每一个下表对应的组合数:
i = 0:只有I型竖放。
i = 1:可以将两条I型竖放或者横放。
i = 3:可以三个I型竖放 + 两I型横放一I型竖放 + 两个L型交叉
我们可以发现L型只会影响两个格所以我们就假设从第三个个字开始进行状态转移,我们可以发现第三个格子存在三种情况:第一种:两个格子都为空,第二种:上格子为空, 第三种:下格子为空,然后我们对着三种情况进行分析:
(1)dp[i][3] = dp[i - 1][3] + dp[i - 1][2] + dp[i - 1][1] + dp[i - 2][3]
这里我当时就有一个疑问:问什么要加上dp[i - 2][3]呢?我们会发现这种情况是有两者不同的方式她的两种方式包含了dp[i - 1][3]的组合:1、当两条I型竖放的时候也就被dp[i - 1][3]包含了,当两条横放的时候就是为考虑到的情况所以要加上这种情况。
(2)dp[i][2] = dp[i - 2][3] + dp[i - 1][1]:
这两种情况就是在i- 2后加上一个L型 + i- 2处一个L型+i- 1处一个横放的I型。
(3)dp[i][1] = dp[i -2][3] + dp[i - 1][2]:
跟第二种情况相似:
明确了dp数组的含义,接下来看初始化:
由于是求组合数所以我们要将dp[0][0]置为1,然后后面的就根据情况来看:dp[0][1]与dp[0][2]为0,
dp[0][3]为1个I型竖放,dp[1][1]与dp[1][2]都为1,dp[1][3]为两I型竖放+两I型横放。dp[1][3] = 2.
接下来求状态转移方程:
也就是上面分析的那样:
(1)dp[i][3] = dp[i - 1][3] + dp[i - 1][2] + dp[i - 1][1] + dp[i - 2][3]
(2)dp[i][2] = dp[i - 2][3] + dp[i - 1][1]:
(3)dp[i][1] = dp[i -2][3] + dp[i - 1][2]:
接下来是遍历顺序:
我们直接从第三个格子开始遍历,在每个循环中分别求出三种情况的dp数组。
下面是完整的AC代码:
#include<bits/stdc++.h>
using namespace std;
const long long mod = 1e9 + 7;
int main(){long long n;cin >> n;long long dp[3][4] = {0};dp[0][3] = 1;dp[1][3] = 2;dp[1][1] = 1;dp[1][2] = 1;for(long long i = 2; i < n; i++){dp[i % 3][3] = (dp[(i - 1) % 3][3] + dp[(i - 1) % 3][1] + dp[(i - 1) % 3][2] + dp[(i - 2) % 3][3]) % mod;dp[i % 3][1] = (dp[(i - 2) % 3][3] + dp[(i - 1) % 3][2]) % mod;dp[i % 3][2] = (dp[(i - 2) % 3][3] + dp[(i - 1) % 3][1]) % mod;}cout << dp[(n - 1) % 3][3] << endl;return 0;
}(9)李白打酒加强版:
题目:
问题描述
话说大诗人李白, 一生好饮。幸好他从不开车。
一天, 他提着酒显, 从家里出来, 酒显中有酒 2 斗。他边走边唱:
无事街上走,提显去打酒。 逢店加一倍, 遇花喝一斗。
这一路上, 他一共遇到店 �N 次, 遇到花 �M 次。已知最后一次遇到的是花, 他正好把酒喝光了。
请你计算李白这一路遇到店和花的顺序, 有多少种不同的可能?
注意: 显里没酒 ( 0 斗) 时遇店是合法的, 加倍后还是没酒; 但是没酒时遇 花是不合法的。
输入格式
第一行包含两个整数 �N 和 �M.
输出格式
输出一个整数表示答案。由于答案可能很大,输出模 1000000007 的结果.
样例输入
5 10

样例输出
14

样例说明
如果我们用 0 代表遇到花,1 代表遇到店,14 种顺序如下:
010101101000000
010110010010000
011000110010000
100010110010000
011001000110000
100011000110000
100100010110000
010110100000100
011001001000100
100011001000100
100100011000100
011010000010100
100100100010100
101000001010100
评测用例规模与约定
对于 40%40% 的评测用例: 1≤�,�≤101≤N,M≤10 。
对于 100%100% 的评测用例: 1≤�,�≤1001≤N,M≤100 。
笔记:
还是一道动态规划的题目不过是维数比较高的:
确定dp数组含义:
dp[i][j][k]:到达经过i个酒店和j个花还剩k斗酒的组合数。
初始化:
dp[0][0][2] = 1,dp[0][0][0] = 1;
状态转移方程:
dp[i][j][k] <----- dp[i - 1][j][k / 2] + dp[i][j - 1][k - 1]
到这里我们可以想到到达经过了i个酒店j个花还剩k斗酒的时候我们要存放的数据不单单只有组合数还有是否能到达该点,所以我们进行特殊判断:
对当前的k只进行判断,如果k值 % 2 == 0 并且i >= 1即上一个经过的地点可以使酒店,如果k值 >= 1并且 j >= 1的话上一个经过的地点就可以是花。由于状态转移方程是:dp[i][j][k] == dp[i - 1][j][k / 2] + dp[i][j - 1][k - 1],所以我们要依次进行这两个判断并将其结果加在原dp[i][j][k]上。
接下来是遍历顺序:由于最后一次遇到的是花,所以花的遍历一定是在店的遍历之后,这样我们才能保证最后一次到的地方是花。
遇到的问题:
(1)为什么最后的结果非要是dp[n][m - 1][1]而不能是dp[n][m][0]呢?
我们要求的正是dp[n][m-1][1]这个状态,表示遇到n次店、m-1次花、剩余1斗酒的方案数。这个状态符合题目"最后一次遇到的是花,他正好把酒喝光了"的要求。
(2)为什么将下面这句代码放在main函数内部就不能正常运行了int n, m, f\[N\]\[N\]\[N\]?
在 C++ 中,局部变量存储在栈上。栈的大小是有限制的,如果你定义的数组太大,就会超出栈的容量,从而导致栈溢出。将该数组声明改为全局变量。
#include<bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
int dp[150][150][150] = {0};// 这里对酒的范围化为了m是因为假设一个店都没有经过那么我们要经过m个花所以要消耗m斗酒
int main(){int m,n;cin >> n >> m;dp[0][0][2] = 1;for(int i = 0; i <= n; i++){for(int j = 0; j <= m - 1; j++){for(int k = 0; k <= m; k++){if(i >= 1 && k % 2 == 0){dp[i][j][k] = dp[i - 1][j][k / 2];}if(j >= 1 && k >= 1){dp[i][j][k] += dp[i][j - 1][k + 1];}dp[i][j][k] = dp[i][j][k] % mod;}}} cout << dp[n][m - 1][1] << endl;return 0;
}(10)砍竹子:
题目:
问题描述
这天, 小明在砍竹子, 他面前有 �n 棵竹子排成一排, 一开始第 �i 棵竹子的 高度为 ℎ�hi.
他觉得一棵一棵砍太慢了, 决定使用魔法来砍竹子。魔法可以对连续的一 段相同高度的竹子使用, 假设这一段竹子的高度为 �H, 那么
用一次魔法可以 把这一段竹子的高度都变为 ⌊⌊�2⌋+1⌋⌊⌊2H⌋+1⌋, 其中 ⌊�⌋⌊x⌋ 表示对 �x 向下取整。小明想 知道他最少使用多少次魔法可
让所有的竹子的高度都变为 1 。
输入格式
第一行为一个正整数 �n, 表示竹子的棵数。
第二行共 �n 个空格分开的正整数 ℎ�hi, 表示每棵竹子的高度。
输出格式
一个整数表示答案。
样例输入
6
2 1 4 2 6 7

样例输出
5

样例说明
其中一种方案:
21426214267→214262→214222→211222→111222→111111→214262→214222→211222→111222→111111共需要 5 步完成
笔记:
先来分析者道题目,我们每次选取最高的那一棵竹子进行处理,如果周围只有他一根高度的那么就只处理这一根,如果周围有连续的竹子一样高,就可以一起处理。由于每次都是处理高度最大的元素,所以我们可以用优先队列来处理:因为我们需要记录竹子的高度以及判断竹子的编号是否连续所以我们就需要设置优先队列元素的类型为pair类型<ll,int>:
注意一点:这里我们安排的顺序也是有考究的:当我们的两棵竹子高度相同时,优先队列就会判断second元素,以second元素为标准再次排出顺序。所以我们要将first设置为高度,second设置为编号,这样我们在处理连续编号进行index -- 遍历的时候就可以进行判断是否连续。
所以这道题就是模拟加优先队列,首先向队列中加入元素,如果元素不是1就直接加入,接着我们用一个while循环来处理队列中的元素,将队首元素取出并分别赋值,将队首元素弹出后我们对该元素进行处理,如果处理后的高度不为1就将处理后的元素加入队列,接着从当前标记开始我们从队列中取出新的对首元素判断是否高度相同且连续。处理为依次队列元素后count++。
#include <iostream>
#include <queue>
#include <cmath>
using namespace std;typedef long long ll;priority_queue<pair<ll, int> > bam;int main() {int count = 0;int n;cin >> n;for (int i = 0; i < n; i++) {ll h;cin >> h;if(h != 1){bam.push(make_pair(h, i));}}while (!bam.empty()) {ll H = bam.top().first;int index = bam.top().second;bam.pop();ll h1 = sqrtl(H / 2 + 1);if (h1 != 1) {bam.push(make_pair(h1, index));}while (!bam.empty() && bam.top().second == index - 1 && bam.top().first == H) {bam.pop();index--;if (h1 != 1) {bam.push(make_pair(h1, index));}}count++;}cout << count << endl;return 0;
}

之事件流事件委托其他事件)


】)
)












)
)