1. 贝塞尔曲线
(1). 贝塞尔曲线的作用
贝塞尔曲线的作用是给定控制点,通过控制点生成对应的曲线进行轨迹拟合,输入为点,输出为受到控制点约束而产生的轨迹。
(2). 贝塞尔曲线的数学表达式
假设给定N个控制点,得到的为N-1阶的贝塞尔曲线,具体如下所示:

综上,可以推导出N+1个点所控制的N阶贝塞尔曲线表达式:

n阶贝塞尔曲线求导后仍然是n-1阶贝塞尔曲线,控制点为原控制点的组合

(3). 伯恩斯坦基多项式

可以看作是二项式展开!!!
n阶伯恩斯坦基多项式求导后仍然是n-1伯恩斯坦基函数

(4). 贝塞尔曲线的性质

(5). 贝塞尔曲线的缺点

2、B样条曲线
下面这个博主视频给我启发很大
详解样条曲线(上)(包含贝塞尔曲线)-CSDN博客

(1). B样条曲线的优点
和Bezier曲线一样也是通过逼近一组控制点来产生曲线,但是B样条多项式的次数可独立于控制点数目(有一定限制),且允许局部控制曲线或曲面。
(2). B样条曲线的数学表达式
假设有N个控制点:

这些控制点用于定义样条曲线的走向、界限分为,则k阶B样条的定义为:

(3). B样条曲线的递推式
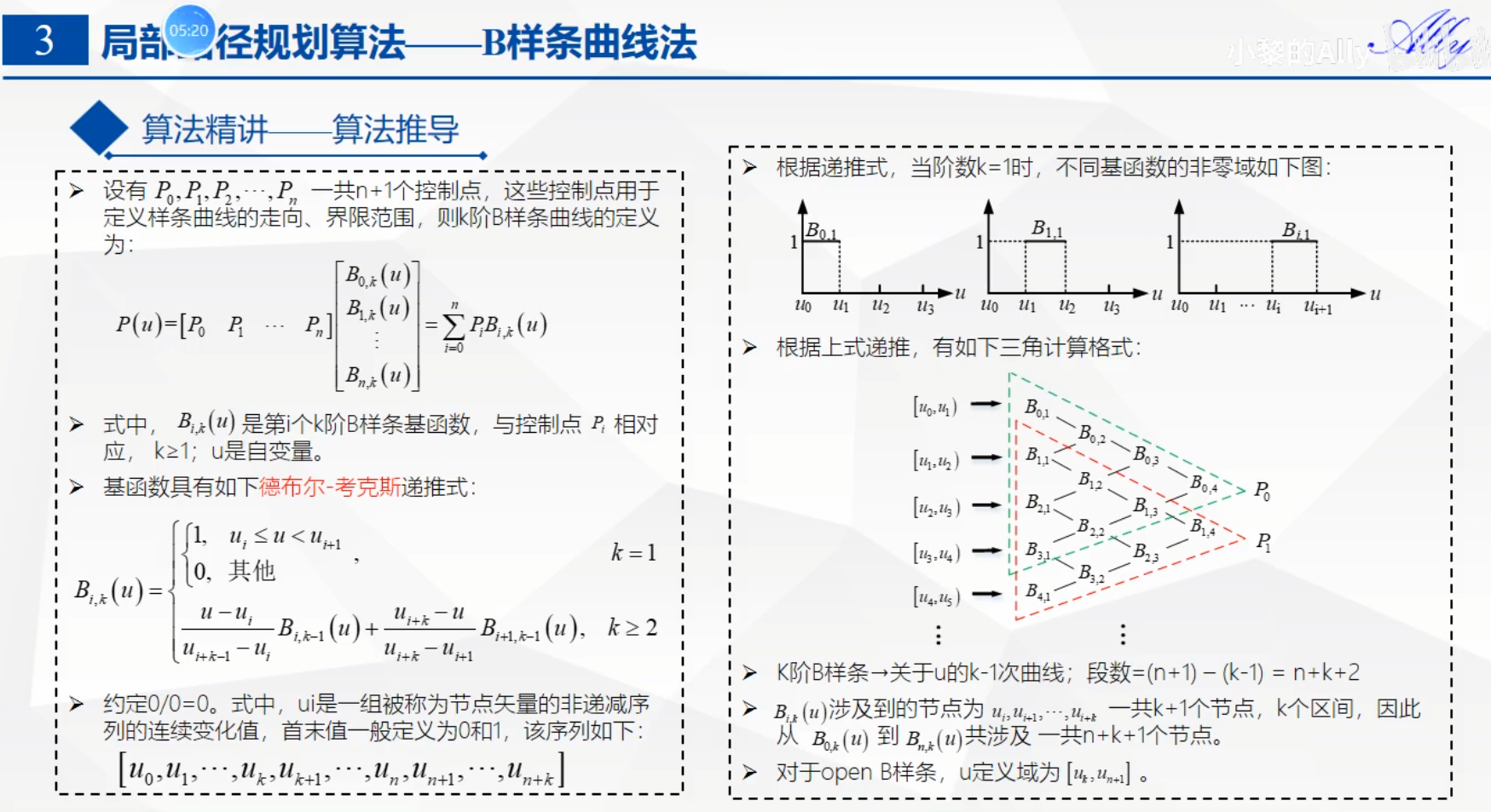
(4). B样条曲线的性质
B样条多项式的次数可独立于控制点的数目(有一定限制),且允许局部控制曲线和曲面生成曲线,本质上是找一组基,各个点是坐标,线性组合。或者理解为在控制点前添加一个权重,然后累加即可。

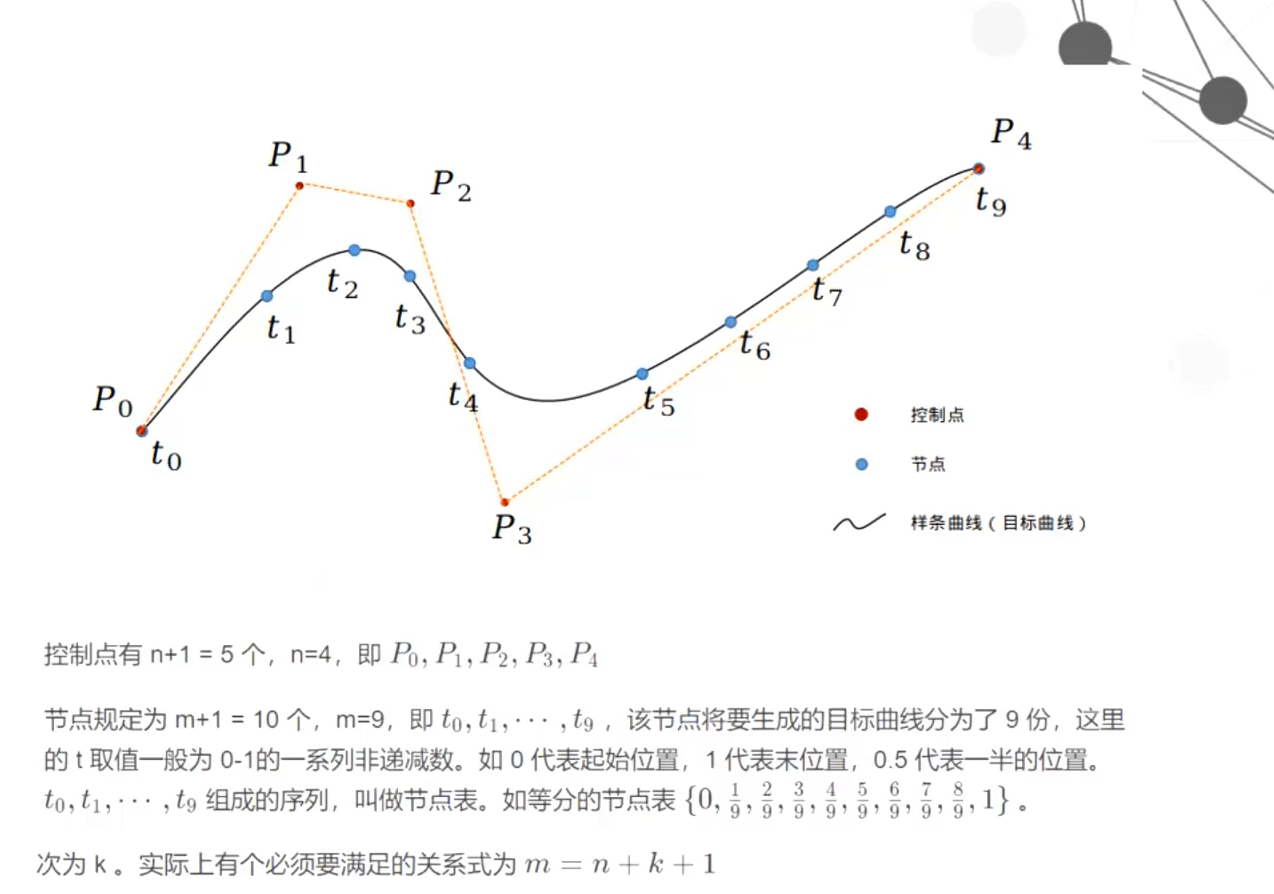






3、B样条的导数
先讲clamped B样条
既然B样条是贝塞尔曲线的扩展,那么必然要继承贝塞尔曲线一些优良的性质。贝塞尔曲线的导数还是贝塞尔, B样条的导数还是B样条。
接下来看推导公式:

B样条公式

基函数求导

基函数求导为低一阶的基函数求导

最终的基函数求导
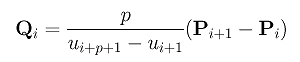
因此,可知,B样条的导数还是B样条, 依然保留B样条的优良特性。
控制点减1,阶数减1,那么节点数目必然是减2. 对于clamped B样条,只要是去除第一个和最后一个节点就ok了,因此clamped B样条的求导还是clamped B样条,这个性质使其方便计算,应用广泛。
4. B样条曲线的应用(Fast-Planner算法)
笔者之前已经深入总结了Fast-Planner算法原理、代码、仿真配置、真机测试的过程,笔记在下面,大家点击跳转即可,吃透Fast-Planner算法基本算是熟练掌握搜索、优化的过程了,希望对大家有所帮助!
(1). Fast算法原理与关键代码
路规算法详细解读(一)—— FAST-Planner重要部分代码解读_fast planner解析-CSDN博客文章浏览阅读1.5k次,点赞7次,收藏26次。由于最近的研究需要,需要对Fast-planner和Ego-planner的代码了解,所以写出这篇代码解读文章,本文持续更新。废话不多说了,上干货!本文基于以下大佬的代码解析基础上去阅读、理解、总结而成。三大主要部分。_fast planner解析https://blog.csdn.net/weixin_43793717/article/details/134360566?spm=1001.2014.3001.5502
(2). Fast算法仿真配置与真机测试
深入解读Fast-Planner算法看这一篇就够!(含Ubuntu20.04 + Ros noetic 环境下 Fast-planner 算法仿真环境的配置与真机效果演示。)_fast planner算法-CSDN博客文章浏览阅读3.6k次,点赞11次,收藏65次。学习Fast-Planner必读文章,本文包含了论文解读、仿真环境配置、真机测试的详细步骤与问题解答,此文是笔者对于Fast-Planner算法理解的叙述与仿真的记录,所有内容皆是原创,假设论文解读已超过万字,所有内容都是笔者一个一个敲出来的,希望对大家理解Fast-Planner算法能够有所帮助。_fast planner算法https://blog.csdn.net/weixin_43793717/article/details/131072185?spm=1001.2014.3001.5501
总结
至此,路径规划——曲线拟合详解结束,到目前为止我们总结了搜索方法、曲线拟合,其实路径规划的核心思想真正意义上来说是优化问题的求解,具体的优化问题解决方法可以跳转到笔者深蓝学院数值优化课程的学习笔记(含有深蓝学院课程PPT),不收费了,大家自取就好。希望笔者的努力能够给入门的朋友带来帮助,如果在看的过程中有什么问题可以留言给笔者,笔者都是手敲内容难免有错,还望大家多多担待~

)





)
:对象To数组——综合应用)


)




)
)

