赛后gym练习及补题,gym链接:2023 (ICPC) Jiangxi Provincial Contest – Official Contest
补题顺序
- L [Zhang Fei Threading Needles - Thick with Fine](https://codeforces.com/gym/104385/problem/L)
- 题面解读
- 参考代码
- A [Drill Wood to Make Fire](https://codeforces.com/gym/104385/problem/A)
- 题面解读
- 参考代码
- B [Wonderful Array](https://codeforces.com/gym/104385/problem/B)
- 题面解读
- 参考代码
- I [Tree](https://codeforces.com/gym/104385/problem/I)
- 题面解读
- 参考代码
- J [Function](https://codeforces.com/gym/104385/problem/J)
- 题面解读
- 参考代码
- K [Split](https://codeforces.com/gym/104385/problem/K)
- 题面解读
- 参考代码
- C [Battle](https://codeforces.com/gym/104385/problem/C)
- 题面解读
- 参考代码
- H [Permutation](https://codeforces.com/gym/104385/problem/H)
- 题面解读
- 参考代码
L Zhang Fei Threading Needles - Thick with Fine
签到题
题面解读
当时在场人数为N,其中夏侯杰被吓死了,其他人被吓跑了,请问张飞吓跑了的人数是多少?
输出N-1即可
参考代码
#include<bits/stdc++.h>
using namespace std;int main()
{ios::sync_with_stdio(0), cin.tie(0);int n; cin >> n;cout << n - 1;return 0;
}
A Drill Wood to Make Fire
签到题
题面解读
钻木取火与钻木的速度与力量有关,当速度与力量的乘积大于某个阈值的时候,能够钻木取火成功。提供阈值、力量、速度,问是否能够取火成功。
参考代码
#include<bits/stdc++.h>
using namespace std;
int n, s, v;int main()
{ios::sync_with_stdio(0), cin.tie(0);int t; cin >> t;while(t--){cin >> n >> s >> v;if(s * v >= n) cout << "1\n";else cout << "0\n";}return 0;
}
B Wonderful Array
数学题
题面解读
给定一个长度为 k 的数组 a ,对于长度为 n 的数组 b :
b i = { x , i = 0 b i − 1 + a i − 1 m o d k , 0 < i ≤ n b_{i}=\begin{cases}x,i=0\\ b_{i-1}+a_{i-1}\quad mod \quad k,0 <i\leq n\end{cases} bi={x,i=0bi−1+ai−1modk,0<i≤n
找出 有多少个 i 使得 :
b i m o d m ≤ b i + 1 m o d m b_{i} \quad mod \quad m\leq b_{i+1}\quad mod \quad m bimodm≤bi+1modm
此处,由于 a[i] 大于 0,所以 b[i] 在不取模情况下一定是一个单调递增的。所以正向考虑满足题意的部分,直接顺序枚举会是一个 O(n) 的复杂度,题目限制 1s ,这样肯定超时。
那么,我们选择反向考虑,寻找能够使得 b[i] > b[i + 1] (取模后)的位置。由于对 m 取模,那么对于一个递增的数组,这个位置就应该每当数组递增超过 m 就出现一次。在整个b数组过程中,就应该有 b[n]/m 个。那么新的问题就是如何去计算 b[n] ?由于 数组 b 一直在对 k 取模,所以 数组 b 是一个周期性增减的,我们就不用去看整个数组b而是找其中一段。计算 数组b[n] 的办法详见代码。
最终答案的个数是 n - b[n]/m。
参考代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int K = 1e6 + 5;ll k, n, m, x;
ll arr[K];int main()
{ios::sync_with_stdio(0), cin.tie(0);cin >> k;for(int i = 0; i < k; ++i) cin >> arr[i];cin >> n >> m >> x;ll b = 0, cnt = 0;x = x % m;for(int i = 0; i < k; ++i) b += arr[i] % m;b = n / k * b + x;for(int i = 0; i < n % k; ++i) b += arr[i] % m;cout << n - b / m;return 0;
}
I Tree
异或
题面解读
一个 n 节点的树,结点连接的边有边权。执行 q 次操作:
- 对结点
x到结点y的路径上每条边的边权异或z。 - 询问编号为
x的结点的所有边的边权异或和。
此处,有个小的脑筋急转弯。比如,对于操作1,如果1-2-3这三个点按照这个顺序连接,当让1到3的路径上边权都异或上 w ,那么此时对于结点 2 ,它所连接的两个边的异或和是没有变化的:比如 1与2的边权为 3 ,2 与 3 的边权大小为 5,对结点 1 到结点 2 的路径上每条边的边权异或 2 ,对于结点2的边权异或和 3 ^ 5 == 3 ^ 2 ^ 5 ^ 2 == 3 ^ 5,因为对于一个数异或自己为0。
那么,操作1的修改只会对 x 和 y 有效。
参考代码
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
int n, q, v[N];
int main()
{ios::sync_with_stdio(0), cin.tie(0);cin >> n >> q;for(int i = 1; i <= n - 1; ++i){int x, y, w;cin >> x >> y >> w;v[x] ^= w, v[y] ^= w;}while(q--){int op; cin >> op;if(op == 1){int x, y, z;cin >> x >> y >> z;v[x] ^= z, v[y] ^= z;}else{int x; cin >> x;cout << v[x] << '\n';}}return 0;
}
J Function
题面解读
给定多个一元二次函数,询问在某一点处的最小值是多少。
当给出一个一元二次函数的时候,我们就可以去通过这个函数去更新其他点上最小值是多少。而如果我们每给出一个函数,就去更新 1 ~ n 上所有点的话,最坏的时间复杂度就是 O(1e10),无法在1s 内跑完。
根据题目中 b b b 的数据范围肯定小于 1e5 ,那么当
( x − i ) 2 > b \left( x-i\right) ^{2} >b (x−i)2>b
此时就不用再去维护这个最小值,因为肯定大于其他函数在这个位置上的最小值。
参考代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e5 + 5;ll arr[N], a, b;
int n, m;
int mxl = int(sqrt(1e5) + 0.5); // 向上取整,大概317void update(int x)
{arr[x] = min(arr[x], b);for(int i = x - 1, j = 1; i >= 1 && j <= mxl; ++j, --i)arr[i] = min(arr[i], j * j + b);for(int i = x + 1, j = 1; i <= n && j <= mxl; ++j, ++i)arr[i] = min(arr[i], j * j + b);
}int main()
{ios::sync_with_stdio(0), cin.tie(0);cin >> n;memset(arr, 0x3f, sizeof arr);for(int i = 1; i <= n; ++i){cin >> b;update(i);}cin >> m;for(int i = 1; i <= m; ++i){int op; cin >> op;if(op){cin >> a; cout << arr[a] << "\n";}else{cin >> a >> b;update(a);}}return 0;
}
K Split
题面解读
题目中给出了一个长度为 n n n 的非增序列。进行 m m m 次操作,分为两种:
操作0,给你一个 1 < x < n 1 <x <n 1<x<n ,使得 a x = a x + 1 + a x − 1 − a x a_{x}=a_{x+1}+a_{x-1}-a_{x} ax=ax+1+ax−1−ax
操作1,将序列分成 k k k 个小块,其中每个小块的最大值-最小值之和要最小,并且输出每个小块中最大值-最小值之和最小值。
对于操作1,随机挑选一段,结果为: a 1 − a i + a i + 1 − . . . − a j + a j + 1 − a n a_1 - a_i + a_{i+1} -... - a_j + a_{j+1} - a_n a1−ai+ai+1−...−aj+aj+1−an, 整理后得: a 1 − a n + a i + 1 − a i + a j + 1 − a j . . . a_1 - a_n + a_{i+1} - a_i + a_{j+1} - a_j ... a1−an+ai+1−ai+aj+1−aj...。可以看出,前两项一定且大于0,后面每两项都是相邻两数之差且小于等于0(后一项-前一项)。因此,为了让最大值减最小值之和最小,我们挑选这个序列中最小的 k − 1 k-1 k−1 个差就可以了。
对于操作0,对序列中某段 a x − 1 , a x , a x + 1 a_{x-1},a_x,a_{x+1} ax−1,ax,ax+1,转变为 a x − 1 , a x + 1 + a x − 1 − a x , a x + 1 a_{x-1},a_{x+1}+a_{x-1}-a_{x},a_{x+1} ax−1,ax+1+ax−1−ax,ax+1。
对于初始情况,这一段的后一项-前一项为: a x − a x − 1 , a x + 1 − a x a_x - a_{x-1},a_{x+1}-a_x ax−ax−1,ax+1−ax,改变之后为: a x − 1 − a x , a x − a x + 1 a_{x-1}-a{x},a_{x}-a_{x+1} ax−1−ax,ax−ax+1。可见,这一波操作并没有对整个序列的差分造成什么影响。所以后续代码中也不会对操作0进行任何处理。
参考代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
typedef long long ll;
int n, m;
ll a[N], b[N];int main()
{ios::sync_with_stdio(0), cin.tie(0);cin >> n;for(int i = 0; i < n; ++i) cin >> a[i];for(int i = 1; i < n; i++) b[i] = a[i] - a[i - 1]; // 计算上述后项与前项的差sort(b + 1, b + n); // 将差分结果排序for(int i = 1; i < n; i++) b[i] = b[i] + b[i - 1]; // 将排序完的结果计算前缀和,方便后续查询直接使用cin >> m;while(m--){int op, k;cin >> op >> k;if(op == 1) cout << a[0] - a[n - 1] + b[k - 1] << "\n"; // 只要选择前 K-1 项即可}return 0;
}
C Battle
题面解读
博弈论中一个经典的Nim游戏,为了补题,专门去看了一眼什么是公平组合游戏。虽然看了,感觉明白了但没完全明白,感兴趣的可以去看看大佬的博客,本蒟蒻还得再吸收理解几遍。
推荐参考理解的博客:算法学习笔记(51): SG函数 、公平组合游戏
参考代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
ll p, ans;ll sg(ll x)
{if(x == p) return 2;if(x&1) return 1;return 0;
}int main()
{ios::sync_with_stdio(false);cin.tie(0);cin >> n >> p;for (int i = 0; i < n; i++){ll t;cin >> t;if (p & 1){if(t&1) ans ^= 1;else ans ^= 0;}else{ans ^= sg(t % (p + 1));}}if(ans) cout << "GOOD\n";else cout << "BAD\n";return 0;
}
H Permutation
多重背包问题
题面解读
给定一个长度为 n n n 的排列(其中 n n n 一定为偶数),现在将其从中间分成两个序列 A A A 和 B B B ,每次执行如下操作:
- 如果序列 A A A 和序列 B B B 都为空,停止操作
- 如果序列 A A A 和 B B B 只有一个为空,将剩余部分放在序列 P P P 的后面
- 如果 A A A 和 B B B 都不为空,将 A A A 和 B B B 首位第一个中最小的一个从原序列中删除,并放入序列 P P P 后面
现在给定序列 P P P,问对于 n n n 的所有排列,是否存在一种使得经过上述操作后成为序列 P P P。
经过观察题面样例可以发现,在排列中,一个数到比其大的数都必须放入一个序列中,如图:
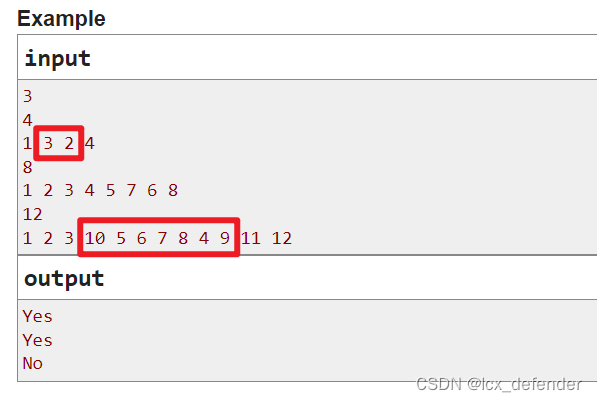
那么就可以将题目中所给序列P按照长度划分为多个物品,每个物品我们需要记录其长度即可,将长度一样的子序列当作同种物品,每种物品有多个。这样,就相当于从这些物品中找到能够凑出长度为 n / 2 n/2 n/2 的方案,多重背包由此得出。
不过此处如果按照普通多重背包去处理,担心可能会超时,所以我们考虑,对于每个物品进行二进制优化(为什么要进行二进制优化可以参考OI-wiki 背包 DP)。
题目中还有一处需要注意的点,就是需要开long long,蒟蒻没有开 long long,喜提 Wrong answer on test 21。
参考代码
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
typedef long long ll;
ll n, arr[N], dp[N];void solve()
{cin >> n;for(int i = 1; i <= n; i++) cin >> arr[i];ll mx = arr[1], cnt = 1, tg = n / 2;map<ll, ll> mp;// 按照规律将数字长度划分到一组中for(int i = 2; i <= n; i++){mx = max(mx, arr[i]);if(mx == arr[i]){mp[cnt]++;cnt = 1;}else{cnt++;if(cnt > tg) { cout << "No\n"; return;}}}mp[cnt]++;// 将长度一样的当作同种物品,按照多重背包二进制优化存储vector<ll> things;for(auto x : mp){cnt = 1;while(x.second >= cnt){things.push_back(x.first * cnt);x.second -= cnt;cnt *= 2;}if(x.second > 0) things.push_back(x.first * x.second);}// 多重背包部分for(int i = 1; i <= tg; ++i) dp[i] = 0;dp[0] = 1;for(int i = 0; i < things.size(); ++i){for(int j = tg; j >= things[i]; --j)dp[j] += dp[j - things[i]];if(dp[tg] >= 1) {cout << "Yes\n"; return;}}cout << "No\n";
}int main()
{ios::sync_with_stdio(0), cin.tie(0);int t; cin >> t;while(t--) solve();return 0;
}




)








)





