题目信息

LeetoCode地址: . - 力扣（LeetCode）

题解内容大量转载于：. - 力扣（LeetCode）

题目理解

题意很直观，就是求二维矩阵中所有元素排序后第k小的数。

最小堆写法

该写法不再赘述，维护一个大小为k的小顶堆，遍历矩阵所有元素进行入堆操作。

时间复杂度:O(nlogk)

空间复杂度:O(k)

class Solution {public int kthSmallest(int[][] matrix, int k) {PriorityQueue<Integer> heap = new PriorityQueue<>((a,b) -> (int)b-(int)a);for (int i = 0; i<matrix.length; i++) {for (int j = 0; j<matrix[0].length;j++) {if (heap.size() < k) {heap.offer(matrix[i][j]);} else if (matrix[i][j] < heap.peek()) {heap.poll();heap.offer(matrix[i][j]);}}}return heap.peek();}
}

二分写法

由于矩阵在行和列上都是有序的，因此左上角的元素matrix[0][0]一定是最小的，右下角的元素matrix[n-1][n-1]一定是最大的。这两个元素，我们分别记为l 和 r.

以下图为例:

可以发现， 任取一个数mid满足l<=mid<=r, 那么矩阵中不大于mid的数，肯定都分布在矩阵的左上角。

例如下图, 取mid=8:

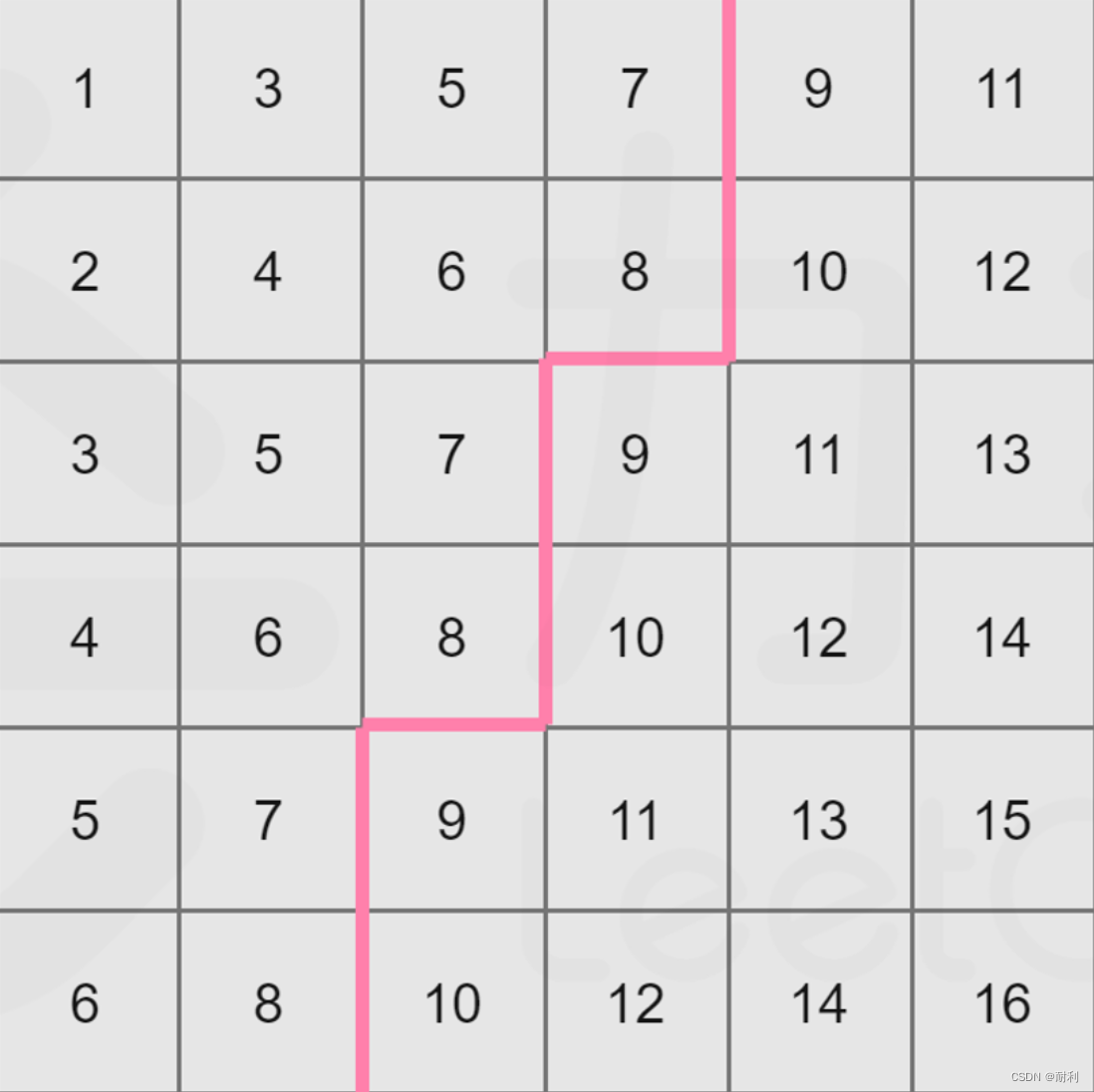
我们可以看出，矩阵中大于mid的数和不大于mid的数分别形成了两个版本，沿着一条锯齿线将这个矩形分隔开。其中左上角板块的大小即为不大于mid的数的数量。

我们只需沿着这条锯齿线走一遍即可计算出这两个板块的大小，自然就统计出这个矩阵中不大于mid的数的个数了。

同样以mid=8举例，走法如下:

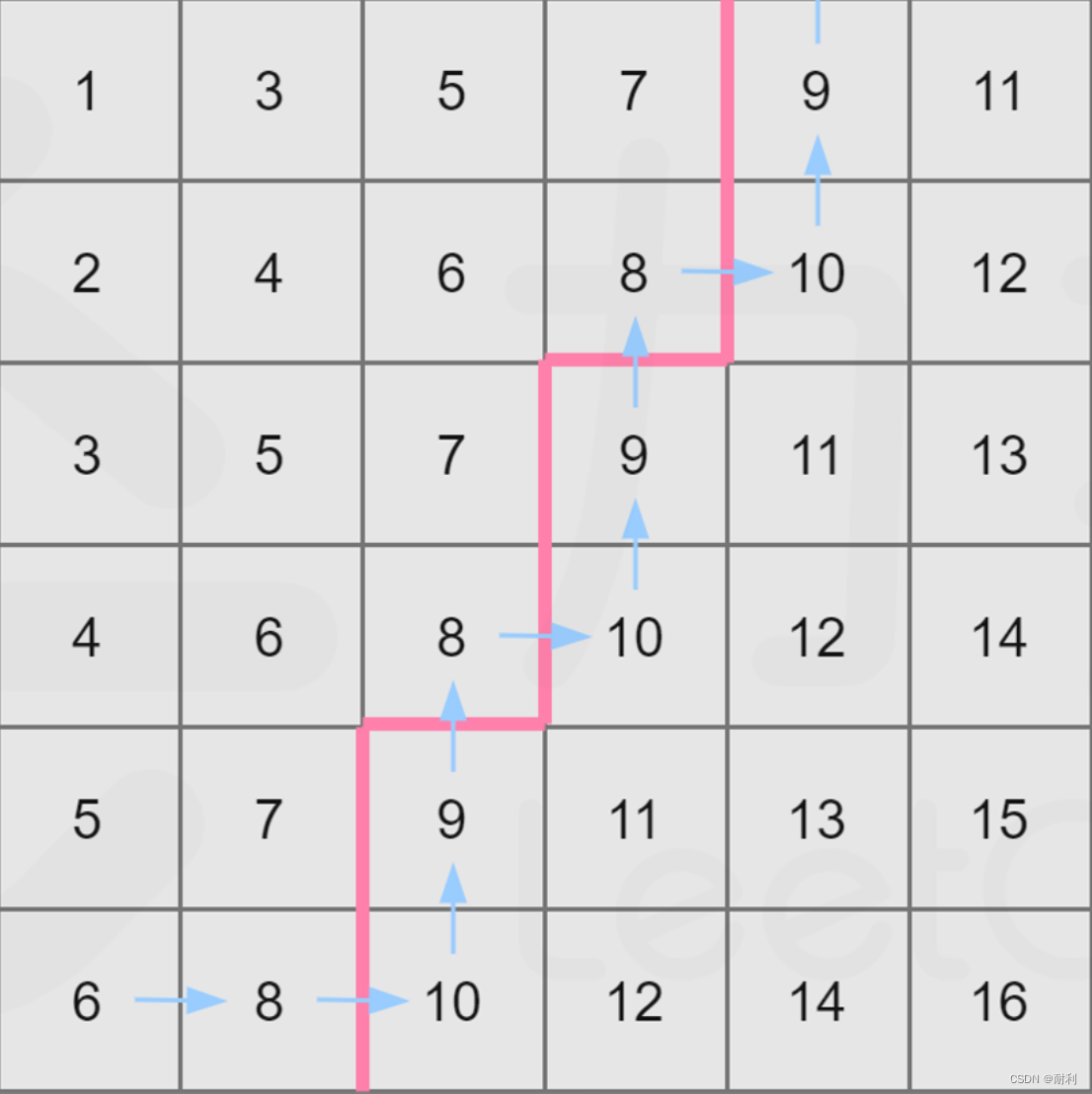
走法可以总结如下:

• 初始位置在matrix[n-1][0] (即左下角);
• 设当前位置为matrix[i][j], 若matrix[i][j] <= mid, 则将当前所在列的不大于mid的数的数量(即i+1)累加到答案中，并向右移动，否则向上移动;
• 不断移动，直到走出格子为止。

可以发现，这样的走法时间复杂度为O(n),即我们可以线性的计算对于任意一个mid,矩阵中有多少数不大于它。这满足了二分查找的性质。

不妨设答案为x, 那么可以直到l<=x<=r, 这样就确定了二分查找的上下界。

对于每次猜测的答案mid, 计算矩阵中有多少数不大于 mid:

• 如果数量不少于k, 那么说明最终答案不大于mid;
• 如果数量小于k, 那么说明最终答案大于mid.

这样我们就可以计算出最终的结果x了。

时间复杂度: O(nlogn)

额外空间复杂度: O(1)

class Solution {public int kthSmallest(int[][] matrix, int k) {int h = matrix.length, w = matrix[0].length;int l = matrix[0][0], r = matrix[h-1][w-1];while (l < r) {int mid = l + (r-l)/2;if (check(matrix, mid, k)) {r = mid;} else {l = mid+1;}}return l;}public boolean check(int[][] matrix,int mid, int k) {int i = matrix.length-1, j = 0;int count = 0;while (i >=0 && j < matrix[0].length) {if (matrix[i][j] <= mid) {count += i+1;j++;} else {i--;}}return count >= k; }
}